1. Общие сведения об интерполяции.
Интерполяция (интерполирование) — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Любителям астрономии часто приходится оперировать именно с дискретными наборами значений, когда необходимо получить значение функции не только для табличных значений аргумента. Например, очень часто требуются координаты Солнца относительно центра Земли, но почти всегда не на 0h всемирного времени, как дается в Астрономических Ежегодниках, а в самые разные моменты времени, которые являются промежуточными между табличными.
В силу сказанного, очень большое практическое значение имеет следующая задача: дана табличная функция; необходимо найти способ приближенного определения значений функции для произвольных значений аргумента, не совпадающих с табличными значениями.
На практике чаще всего применяют интерполяцию многочленами. Это связано прежде всего с тем, что многочлены легко вычислять и легко аналитически находить их производные. К указанным методам относят:
- Метод линейной интерполяции;
- Интерполяционный метод Ньютона;
- Метод конечных разностей;
- Метод интерполяции многочленом Лагранжа;
- Метод интерполяции Эйткена;
- Метод интерполяции кубическим сплайном.
Поскольку в обработке реализована именно интерполяция кубическим сплайном, имеет смысл остановиться на этом методе более подробно.
2. Интерполяция сплайном третьего порядка.
Пусть на некотором отрезке в точках x0, x1, x2, ... xN известны значения функции f(x), а именно y0, y1, y2, ... yN. Требуется построить интерполирующую функцию F(x), такую, что бы она принимала в указанных точках те же значения: F(x0) = y0, F(x1) = y1, ... F(xN) = yN.
Геометрически это значит, что нужно найти такую кривую y = F(x), которая проходит через систему заданных точек.
Очевидно, что данная задача может иметь либо бесчисленное множество решений, либо совсем не иметь решений. В случае интерполяции сплайном кривая F(x) состоит из кусочков, причем на каждом отрезке [xk-1; xk] функция F(x) представляет собой кубический полином вида Fk(x) = ak + bk(x-xk) + ck(x-xk)2 + dk(x-xk)3. При этом:
F = F1 на интервале [x0, x1]
F = F2 на интервале [x1, x2]
...
F = FN на интервале [xN-1, xN]
При этом, на каждом из отрезков [xk-1; xk] коэффициенты полинома ak, bk, ck, dk принимают разные значения.
Чтобы вычислить эти коэффициенты, кроме условия непрерывности функции на полиномы следует наложить дополнительные условия – во-первых, условие непрерывности первой и второй производной функции F(x), во-вторых, условие равенства вторых производных функции на концах отрезка [x0; xN], т.е.
Fk-1(xk-1) = Fk(xk-1),
F'k-1(xk-1) = F'k(xk-1),
F''k-1(xk-1) = F''k(xk-1),
F''(x0)=0, F''(xN)=0.
(k=2,3,..N )
Выражения для производных функций Fk принимают вид:
F'k(x) = bk + 2ck(x - xk) + 3dk(x-xk)2
F''k(x) = 2ck + 6 dk(x-xk)
Если подставить эти выражения в условия непрерывности, то можно получить следующую систему:
a1 - b1h1 + c1h12 - d1h13 = y0
ak = yk, k=1,2,..N
ak-1 = ak - bkhk + ckhk2 - dkhk3, k=2,3...N
bk-1 = bk - 2ckhk + 3dkhk2, k=2,3...N
ck-1 = ck - 3dkhk, k=2,3...N
c1 - 3d1h1 = 0
cN = 0,
где hk = xk - xk-1, k=1,2,...N
Пусть lk = (yk - yk-1)/hk, k=1,2,...N, а c0 = 0 .
Тогда представленную выше систему уравнений можно решить с помощью метода прогонки:
δ1 = - h2/(2(h1+h2))
λ1 = 3(l2 - l1)/(2(h1+h2))
δk-1 = - hk/(2hk-1+2hk+hk-1δk-2), k=3,4, ... N
λk-1 = (3lk - 3lk-1 - hk-1λk-2)/(2hk-1+2hk+hk-1δk-2)
При этом коэффициенты ck находятся по формулам обратной прогонки:
ck-1 = δk-1ck + λk-1, k = N, N-1, N-2, ... 2
После нахождения ck вычисление коэффициентов bk и dk не представляет труда:
bk = lk + (2ckhk + hkck-1)/3, k=1,2,...N
dk = (ck - ck-1)/(3hk), k=1,2,...N
Источник: http://www.alexeypetrov.narod.ru/C/spline_about.html
3. Выполнение интерполяции.
Источником для интерполирования являются данные, загруженные в таблицу «Исходные данные». Формирование этой таблицы может осуществляться в двух режимах:
- В ручном режиме – путем активирования управляющей кнопки «Добавить», расположенной в командной панели табличной части;
- В режиме автоматизированной загрузки данных, записанных в файл Excel – путем активизации управляющей кнопки «Загрузить», расположенной в командной панели формы.
При использовании метода автоматизированной загрузки данных пользователю открывается диалог выбора исходного файла (см. рис.). После выбора файла и активации управляющей кнопки «Открыть» для пользователя становятся доступны следующие реквизиты группы «Параметры расчета»:
- Номер листа: определяет порядковый номер листа с загружаемыми данными в рабочей книге Excel. Нумерация листов начинается с единицы;
- Начальная строка: определяет порядковый номер первой строки листа, с которой будет осуществлена загрузка данных. Нумерация строк начинается с единицы;
- Колонка аргумента: порядковый номер колонки листа, которая содержит массив загружаемых значений аргументов;
- Колонка функций: порядковый номер колонки листа, которая содержит массив загружаемых значений функций.
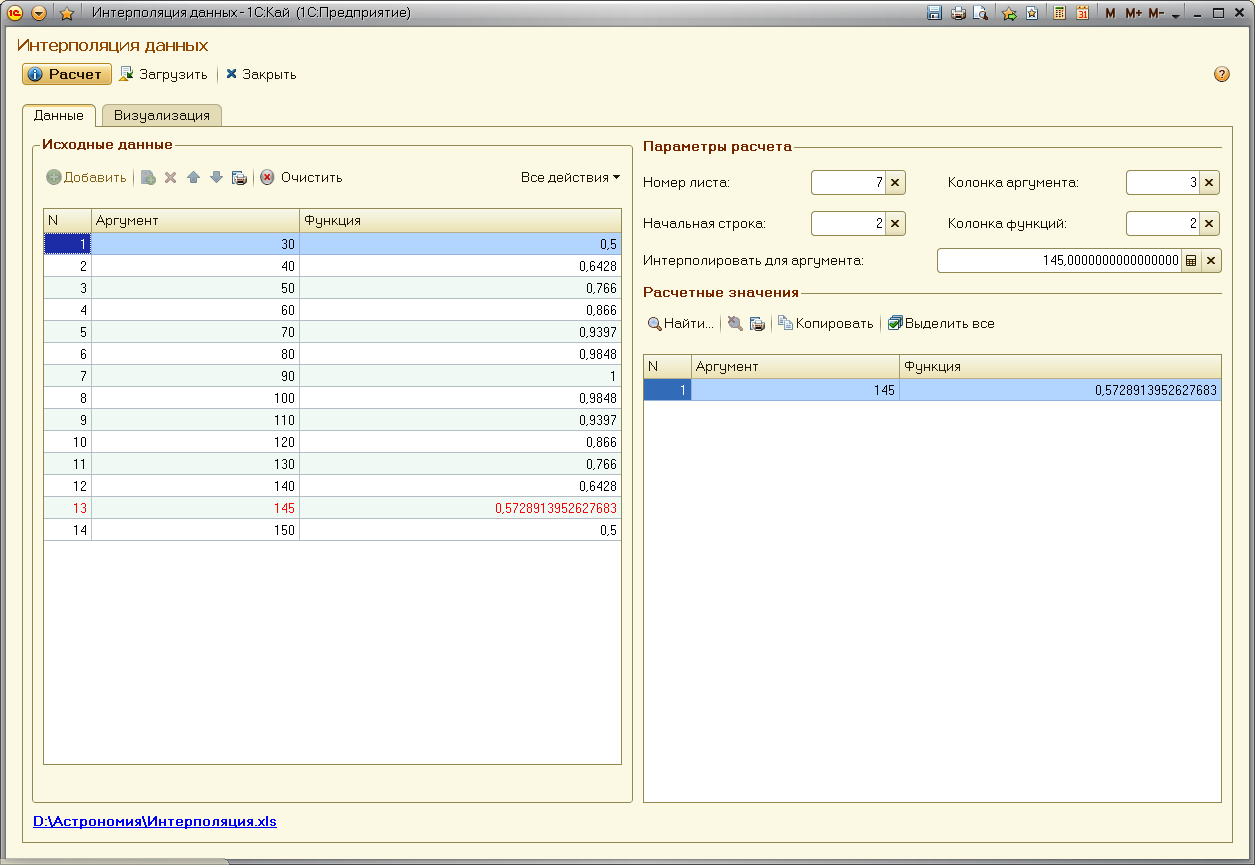
Если параметры расчета сформированы не корректно, система предупредит об этом пользователя, в противном случае, все загружаемые из листа рабочей книги Excel данные станут доступны для просмотра в таблице «Исходные данные» формы (см. Рис. 1). Для того, что бы получить интерполируемое значение функции, необходимо в реквизите «Интерполировать для аргумента» указать значение выбранного аргумента, и активизировать управляющую кнопку «Расчет» (см. Рис. 2). При этом найденное значение будет добавлено в таблицу «Расчетные значения», и в таблицу «Исходные данные», причем в последней таблице добавленная строка выделяется красным шрифтом.
4. Визуализация.
С целью наглядного представления поведения функции для пользователя доступна функциональность элементов управления, представленных на закладке «Визуализация» (см. Рис. 3). К сожалению, платформа не обеспечивает возможность работы с диаграммами и графиками в той степени, в которой это необходимо для любителя астрономии. В силу сказанного, процедура построения графика, и параметров его отображения реализована средствами https://google-developers.appspot.com/chart/interactive/docs/index. Посредством внедренных в конфигурацию скриптов, пользователь имеет возможность изменять цвет и ширину линии графика, устанавливать шрифт подписей, размер отображаемых точек, изменять ориентацию осей диаграммы, и т.п. При конвертации цвета автором была использована методика Михаила Журавлева (см. //infostart.ru/public/115963/).