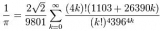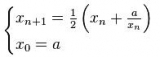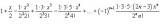В воспоминаниях Ричарда Фейнмана есть такой эпизод.
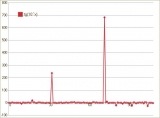
” Пол проходит по столовой, где все просто стоят на ушах. “Эй, Пол! – кричат они. – Фейнман – просто супер! Мы даем ему задачу, которую можно сформулировать за десять секунд, и он за одну минуту дает ответ с точностью до 10 процентов. Дай ему какую-нибудь задачу!” Почти не останавливаясь, он говорит: “Тангенс 10 градусов в сотой степени”. Я влип: для этого нужно делить на число пи до ста десятичных разрядов! Это было безнадежно!”.
В приведенном фрагменте переводчик ошибся. Пол Олам просит Фейнмана вычислить тангенс числа 10 в сотой степени. И речь идет о радианах, а не градусах. Именно в такой формулировке задача становится неподъемной для будущего нобелевского лауреата.
В уме такое решить нельзя, зато оказывается подобные расчеты можно провести с помощью 1С. Автором формулы, которую я использовал является поразительный индийский математик Рамануджан. Не буду излагать его жизнь и результаты, все это есть в Сети. Скажу только, что это удивительный человек, который образно говоря, «разговаривал» с числами, причем каждое натуральное число было его личным другом. Будучи очень религиозным человеком, Рамануджан, по видимому, видел в мире чисел и в отношениях, которыми этот мир пронизан, проявление божественной гармонии и красоты. И раз Всевышний говорит с нами через откровения, то такой же подход Рамануджан использовал к изучению математики. «Его понимание сущности математического доказательства было более чем туманным; он пришел ко всем своим результатам, как ранним, так и более поздним, как верным, так и неверным, при помощи странной смеси интуитивных догадок, индуктивных соображений и логических рассуждений». Так говорил его современник. А теперь формула Рамануджана:
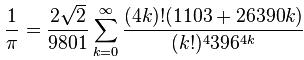
С моей точки зрения это что-то невозможное! Обычный человек не в состоянии прийти к такому выражению. При этом надо учесть, что до 27 лет Рамануджан занимался математикой сам для себя, не имея контакта с серьезными специалистами.
Все расчеты я проводил на платформе 1С: Предприятие, редакция 8.2. Спасибо разработчикам, что они реализовали в программе длинную математику для умножения и сложения, это очень упрощает жизнь. Для деления есть ограничение в 27 знаков после запятой, поэтому деление пришлось реализовать самому. Но обо всем по порядку.
Первая задача – уметь вычислять √2 с любой точностью. Для этого обычно ищут ноль следующей функции:
f(x)=x²-2,
С этой целью используют итерационную формулой Герона, в которой a=2:
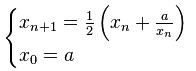
Но если у вас нет длинного деления, когда вы можете указать количество значащих цифр после запятой, то точность вычислений по данной формуле будет ограничиваться точностью деления, которая реализована в системе. В 1С это 27 знаков и именно такую минимальную погрешность я смог получить. Тогда я решил проверить, как будет работать разложение в ряд Тейлора для функции квадратный корень из (1+х). Ниже приводится соответствующая формула для разложения.
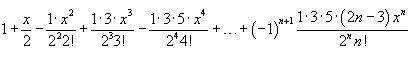
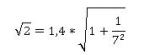
Отметим, что каждый последующий член ряда отличается от предыдущего знаком и коэффициентом 0.5*x*(2-3/n). Корень из двух я планировал получить, используя тождество:
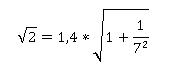
С этой целью значение ряда вычислим в точке 1/49. Для того, чтобы обойти ограничения на точность конечного результат от представления результатов деления, число 1/49 будем представлять следующим образом. Дробь 1/7 имеет период 142857, поэтому сначала сформируем десятичную запись данной дроби с количеством знаков после запятой, которое определяется требуемой точностью расчетов, затем полученное значение умножим само на себя. А вот множитель (2-3/n) я оставил таким, какой он есть. Формула готова осталось проверить, как она работает. Результат я сравнивал с данными, которые выдает www.wolframalpha.com. Для точности в 100 знаков после запятой потребовалось 57 членов ряда, результат совпал с эталонным значением. По-видимому, я стал первым человеком на планете, который провел вычисление корня из двух в 1С с такой точностью.

Это был первый шаг к использованию формулы Рамануджана. Последующие эксперименты показали, что без реализации длинного деления продвинуться за 27 значащих цифр нельзя. Поэтому я написал функцию ДлинноеДеление, которая вычисляет дробь 1/x, где натуральное число х это первый аргумент функции, а количество знаков после запятой — второй. Проверку правильной работы данного алгоритма рекомендую проводить на выражении 1/9801, результат некоторых думаю удивит.
Функция ДлинноеДеление(вхЗнаменатель,вхТочность) экспорт
перем выхРезультат;
если вхЗнаменатель=1 тогда
возврат 1;
конецесли;
выхРезультат=новый массив;
мЧислитель=10;
пока Истина цикл
пока мЧислитель=вхЗнаменатель цикл
мЧислитель=мЧислитель-вхЗнаменатель;
число=число+1;
конеццикла;
пока число<>0 цикл
остаток=число%10;
выхРезультат.Добавить(остаток);
число=(число-остаток)/10
конеццикла;
если мЧислитель=0 тогда
прервать;
конецесли;
если выхРезультат.Количество()>=вхТочность тогда
прервать;
конецесли;
мЧислитель=мЧислитель*10;
конеццикла;
результат=0;
разряд=0.1;
для каждого цифра из выхРезультат цикл
результат=результат+разряд*цифра;
разряд=разряд*0.1;
конеццикла;
возврат результат;
КонецФункции
Теперь формула, которую открыл Сриниваса Рамануджан Айенгор показала всю свою мощь. Проверка полученного числа проводилась опять с помощью www.wolframalpha.com.

После этого уже не было никаких преград для определения значения tg(10¹ºº). Попытаемся сделать устную оценку. В выражении (10¹ºº/пи)*пи я отбросил целое количество пи, и оставил 0.12*пи. Первый член в разложении tg(x), который равен х, дает нам следующее приблжение:
0.12*пи=3/25*пи≈3*1/8=3*0,125=0,375.
Если учесть второй член разложения, то к приведенному значению надо будет добавить (0,375)³/3. Заменяем выражение в скобках на 0.4, выполняем элементарные операции и получаем 0,021. Тогда уточненная оценка будет 0,396. На этом и остановимся.
Данная статья является примером того, как в 1С выполнять вычисления с любой заданной точностью. Оказывается, что при небольших усилиях длиную математику можно реализовать и на данной платформе. Для меня это было небольшим открытием, которым я и поделился.