Допустим, организация ведет учет транспортных расходов отдельно от стоимости перевозимых товаров.
Весь учет ведется в некотором регистре остатков
Измерения:
- Склад
- Номенклатура
Ресурсы:
- Количество (количество перевезенных товаров)
- Сумма (сумма понесенных транспортных расходов)
Реквизиты
- Вид операции
Транспортные расходы возникают при проведении документа «Расходный ордер на товары»
Сумму транспортных расходов нужно распределять по некоторым операциям, например:
- Реализация,
- Комплектация,
- Переработка,
- Перемещение
Распределение производится за месяц последним днем месяца.
Представим операции за период в виде схемы...
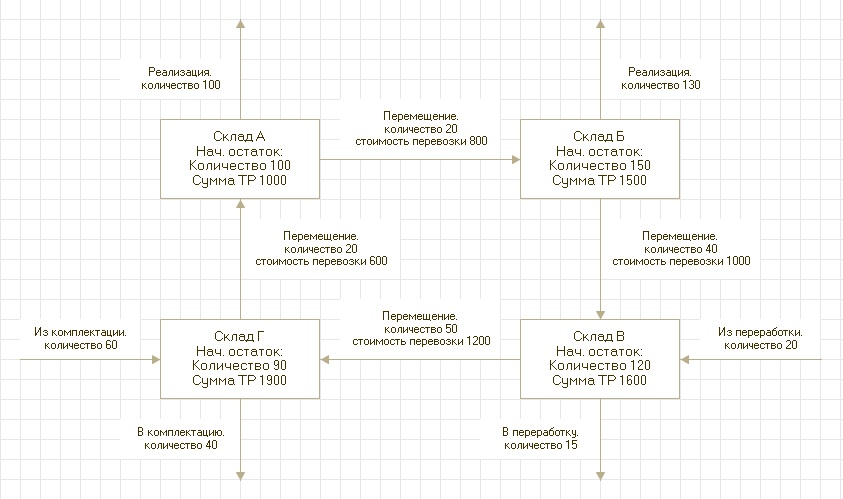
... и в виде таблицы.
Остатки на начало периода: Сумма - остаток нераспределенных транспортных расходов, Количество - остаток товара на складе.
| Период | Склад | Количество | Сумма ТР |
| 01.07.2014 | А | 100 | 1000 |
| 01.07.2014 | Б | 150 | 1500 |
| 01.07.2014 | В | 120 | 1600 |
| 01.07.2014 | Г | 90 | 1900 |
Операции, на которые нужно распределить сумму ТР:
| Период | Документ | Операция |
Склад отпр |
Склад получ |
Количество | Сумма ТР |
| 05.07.2014 | Расходный ордер №1 | Перемещение | А | Б | 20 | 800 |
| 10.07.2014 | Расходный ордер №2 | Перемещение | Б | В | 40 | 1000 |
| 11.07.2014 | Комплектация номенклатуры №1 | Комплектация | Г | 60 | ||
| 12.07.2014 | Расходный ордер №3 | Перемещение | В | Г | 50 | 1200 |
| 13.07.2014 | Комплектация номенклатуры №2 | Комплектация | Г | 40 | ||
| 16.07.2014 | Расходный ордер №4 | Перемещение | Г | А | 20 | 600 |
| 17.07.2014 | Передача товаров №1 | Переработка | В | 15 | ||
| 18.07.2014 | Поступление товаров из пер-ки№1 | Переработка | В | 20 | ||
| 20.07.2014 | Реализация товаров и услуг №1 | Реализация | А | 100 | ||
| 25.07.2014 | Реализация товаров и услуг №2 | Реализация | Б | 130 |
Решение.
В целом решение будет состоять из следующих шагов:
1. Составить таблицу движений
2. Составить таблицу СЛАУ
3. Решить СЛАУ
4. Подставить в таблицу движений полученные значения суммы ТР на единицу для каждого склада (стоимость выбытия)

1. Составляем таблицу движений
Не важно как, дополним исходную таблицу строками движений на основе операций. Должно получиться это:
| № | Период | Операция | Склад |
Корр склад |
Количество приход |
Количество расход |
Сумма ТР приход |
Сумма ТР расход |
| 1 | 01.07.2014 | Сальдо | А | 100 | 1000 | |||
| 2 | 01.07.2014 | Сальдо | Б | 150 | 1500 | |||
| 3 | 01.07.2014 | Сальдо | В | 120 | 1600 | |||
| 4 | 01.07.2014 | Сальдо | Г | 90 | 1900 | |||
| 5 | 05.07.2014 | Перемещение | Б | А | 20 | 800 | ||
| 6 | 05.07.2014 | Перемещение | А | 20 | ||||
| 7 | 10.07.2014 | Перемещение | В | Б | 40 | 1000 | ||
| 8 | 10.07.2014 | Перемещение | Б | 40 | ||||
| 9 | 11.07.2014 | Комплектация | Г | 60 | ||||
| 10 | 12.07.2014 | Перемещение | Г | В | 50 | 1200 | ||
| 11 | 12.07.2014 | Перемещение | В | 50 | ||||
| 12 | 13.07.2014 | Комплектация | Г | 40 | ||||
| 13 | 16.07.2014 | Перемещение | А | Г | 20 | 600 | ||
| 14 | 16.07.2014 | Перемещение | Г | 20 | ||||
| 15 | 17.07.2014 | Переработка | В | 15 | ||||
| 16 | 18.07.2014 | Переработка | В | 20 | ||||
| 17 | 20.07.2014 | Реализация | А | 100 | ||||
| 18 | 25.07.2014 | Реализация | Б | 130 | ||||
| 19 | 31.07.2014 | Сальдо | А | 0 | ||||
| 20 | 31.07.2014 | Сальдо | Б | 0 | ||||
| 21 | 31.07.2014 | Сальдо | В | 105 | ||||
| 22 | 31.07.2014 | Сальдо | Г | 140 |
2. Составление таблицы СЛАУ
Далее нужно будет составить систему линейных уравнений баланса этой таблицы. Решив эту систему, мы сможем получить стоимость списания транспортных расходов с каждого склада.
Уравнения будут такие:
для склада А: 1000 - 20*А + 20 *Г + 600 – 100 * А = 0*А
для склада Б: 1500 + 20*А + 800 – 40*Б – 130*Б = 0*Б
для склада В: 1600 + 40 *Б + 1000 – 50*В + 15*В – 20*В = 105*В
для склада Г: 1900 + 60*Г + 50*В + 1200 – 40*Г –20*Г = 140*Г
Где множители А,Б,В,Г – это неизвестная стоимость списания ТР на единицу товара с одноименного склада.
Упростим эти уравнения, также переместив все свободные члены (без множителей) за знак равенства.
Получим такую систему уравнений:
для склада А: -120*А + 20 *Г = -1600
для склада Б: 20*А – 170*Б = -2300
для склада В: 40 *Б – 160*В = -2600
для склада Г: 50*В - 140*Г = -3100
Теперь опишем эти уравнения в виде таблицы, полученной из таблицы движений:
| № | Склад | А | Б | В | Г | Свободный член |
| 1 | А | -1000 | ||||
| 2 | Б | -1500 | ||||
| 3 | В | -1600 | ||||
| 4 | Г | -1900 | ||||
| 5 | Б | 20 | -800 | |||
| 6 | А | -20 | ||||
| 7 | В | 40 | -1000 | |||
| 8 | Б | -40 | ||||
| 9 | Г | 60 | ||||
| 10 | Г | 50 | -1200 | |||
| 11 | В | -50 | ||||
| 12 | Г | -40 | ||||
| 13 | А | 20 | -600 | |||
| 14 | Г | -20 | ||||
| 15 | В | 15 | ||||
| 16 | В | -20 | ||||
| 17 | А | -100 | ||||
| 18 | Б | -130 | ||||
| 19 | А | 0 | ||||
| 20 | Б | 0 | ||||
| 21 | В | -105 | ||||
| 22 | Г | -140 |
|
Свернем таблицу по складу. Получим систему уравнений в виде таблицы:
| Склад | А | Б | В | Г | Свободный член |
| А | -120 | 20 | -1600 | ||
| Б | 20 | -170 | -2300 | ||
| В | 40 | -160 | -2600 | ||
| Г | 50 | -140 | -3100 |
3. Решение СЛАУ
Теперь эту систему нужно решить. Каким образом?
Любой метод решения СЛАУ даст результаты, разной степени точности.
Используем метод Гаусса с выделением главного элемента. Он считается самым точным, однако «при большом числе уравнений метод может стать слишком сложным».
И метод простых итераций.
Метод Гаусса
Для начала нужно привести матрицу к диагональному виду, т.е отсортировать строки таким образом, чтобы на диагонали располагался максимальный по модулю элемент столбца. Это и есть «выделение главного члена». В нашем примере матрица и так уже отсортирована как надо.
Затем для каждой строки (n) матрицы находим коэффициент путем деления последующих элементов столбца (n) на главный элемент (тот, что на диагонали).
На полученный коэффициент умножаем всю строку (n) и вычитаем ее из всех последующих строк матрицы.
Получим матрицу такого треугольного вида:
| А | Б | В | Г | Свободный член |
| -120 | 0 | 0 | 20 | -1600 |
| 0 | -170 | 0 | 3,3333 | -2566,67 |
| 0 | 0 | -160 | 0,78 | -3203,92 |
| 0 | 0 | 0 | -139,75 | -4101,23 |
Далее будем вычислять значение неизвестных, начиная с самой нижней строки:
Г) Г = -4101,23 / -139,75 = 29,3458435637;
В) В = (-3203,92 - 0,78*29,3458435637) / -160 = 20,1683619783;
Б) Б = (-2566,67 – 3,33*29,3458435637– 0 * 20,1683619783) / -170 = 15,6734479130;
А) А = (-1600 – 20 * 29,3458435637–0 * 20,1683619783- 0 * 15,6734479130) / -120 = 18,2243072606;
Код такой:
Функция РешитьМетодомГауса (Матрица)
Если Матрица= Неопределено Тогда
Возврат Неопределено;
КонецЕсли;
КоличествоСтрок=Матрица.Количество();
КоличествоСтолбцов=Матрица[0].Количество();
МассивКоэффициентов= Новый Массив(КоличествоСтрок);
Для Стр= 0 По КоличествоСтрок-2 Цикл
//Поиск максимального элемента в столбце
МаксимальныйЭлементСтолбца=Матрица[Стр][Стр];
НомерСтрокиМаксЭлемента=Стр;
Для ПодСтр=Стр По КоличествоСтрок-1 Цикл
Если МодульЧисла(Матрица[ПодСтр][Стр])>МодульЧисла(МаксимальныйЭлементСтолбца)Тогда
МаксимальныйЭлементСтолбца=Матрица[ПодСтр][Стр];
НомерСтрокиМаксЭлемента=ПодСтр;
КонецЕсли;
КонецЦикла;
//Система не разрешима если максимальный элемент равен нулю
Если МаксимальныйЭлементСтолбца= 0 Тогда
Возврат Неопределено;
КонецЕсли;
//Меняем текущую строку со строкой с максимальным элементом
Если НомерСтрокиМаксЭлемента<>Стр Тогда
Для Стб= 0 По КоличествоСтолбцов-1 Цикл
Буфер=Матрица[Стр][Стб];
Матрица[Стр][Стб]=Матрица[НомерСтрокиМаксЭлемента][Стб];
Матрица[НомерСтрокиМаксЭлемента][Стб]=Буфер;
КонецЦикла;
КонецЕсли;
//Вычисляем коэффициенты для каждой строки
Для ПодСтр= 0 По КоличествоСтрок-2-Стр Цикл
МассивКоэффициентов[Стр+1+ПодСтр]=Матрица[Стр+1+ПодСтр][Стр]/Матрица[Стр][Стр];
КонецЦикла;
//Вычитание строк
Для ПодСтр=Стр+1 По КоличествоСтрок-1 Цикл
Для Стб=Стр По КоличествоСтолбцов-1 Цикл
Матрица[ПодСтр][Стб]=Матрица[ПодСтр][Стб]–МассивКоэффициентов[ПодСтр]*Матрица[Стр][Стб];
КонецЦикла;
КонецЦикла;
КонецЦикла;
//Вычисление корней СЛАУ обратным ходом
Решение= Новый Массив(КоличествоСтрок);
Для Стр=-КоличествоСтрок+1 По0 Цикл
Если Стр=-КоличествоСтрок+ 1 Тогда// первый виток
Решение[-Стр]=Матрица[-Стр][КоличествоСтолбцов-1]/Матрица[-Стр][-Стр];
Иначе
Для ПодСтр=-Стр+1 По КоличествоСтрок-1 Цикл
Матрица[-Стр][КоличествоСтолбцов-1]=Матрица[-Стр][КоличествоСтолбцов-1]- Решение[ПодСтр]*Матрица[-Стр][ПодСтр];
КонецЦикла;
Решение[-Стр]=Матрица[-Стр][КоличествоСтолбцов-1]/Матрица[-Стр][-Стр];
КонецЕсли;
КонецЦикла;
Возврат Решение;
КонецФункции
Функция МодульЧисла(Число)
Возврат ?(Число >0,Число,-Число);
КонецФункцииМетод простых итераций
Приводим матрицу к диагональному виду, как и в методе Гаусса. В нашем примере матрица и так уже отсортирована как надо.
| А | Б | В | Г | Свободный член |
| -120 | 0 | 0 | 20 | -1600 |
| 20 | -170 | 0 | 0 | -2300 |
| 0 | 40 | -160 | 0 | -2600 |
| 0 | 0 | 50 | -140 | -3100 |
Для каждой строки матрицы элемент Хnна диагонали меняем местами со свободным членом, меняя и знак.
Уравнения будут выглядеть так:
А) 1600 + 0 * Б + 0 * В + 20 * Г = 120 * А
Б) 20 * А + 2300 + 0 * В + 0 * Г = 170 * Б
В) 0 * А + 40 * Б + 2600 - 105 * Г = 55 * В
Г) 0 * А + 0 * Б + 50 * В + 3100 = 140 * Г
.. и разделим каждое уравнение на коэффициент в правой части уравнений:
А) 13,33 + 0 *Б + 0 * В + 0,17 * Г = А
Б) 0,12 *А + 13,53 + 0 * В + 0 * Г = Б
В) 0 * А + 0,73 * Б + 47,27 - 1,91 * Г = В
Г) 0 * А + 0 * Б + 0,36 * В + 22,14 = Г
Проще говоря, мы разрешили каждое уравнение (n) относительно Хn.
Матрица примет вид:
| А | Б | В | Г | Свободный член |
| 13,333333333 | 0 | 0 | 0,166666667 | 1 |
| 0,117647059 | 13,529411765 | 0 | 0 | 1 |
| 0 | 0,727272727 | 47,272727273 | -1,909090909 | 1 |
| 0 | 0 | 0,357142857 | 22,142857143 | 1 |
Затем весь процесс выглядит так:
О итерация - Подставляем в каждое уравнение значение неизвестных (А,Б,В,Г) равными 0, получаем первое решение
1 итерация – подставляем в
каждое уравнение значение неизвестных (А,Б,В,Г), рассчитанные на предыдущей итерации
- рассчитываем
погрешности для каждого неизвестного вычитанием текущего решения из предыдущего.
- сравниваем
максимальное значение погрешности с заданной точностью. Если погрешность меньше, тогда решение
найдено.
И так далее, пока не будет найдено решение.
Опытным путем была подобрана точность решения, равная 0,0000001, при которой решение методом итераций дает результат вычисления сильно приближенный к решению методом Гаусса.
Результат метода итераций такой:
А = 18,2243072542
Б = 15,6734479099
В = 20,1683619754
Г = 29,3458435562
Код метода такой:
Функция РешитьМетодомИтераций(Матрица)
Если Матрица=НеопределеноТогда
Возврат Неопределено;
КонецЕсли;
Если Точность= 0 Тогда
Сообщить("Не указана точность вычислений.");
Возврат Неопределено;
КонецЕсли;
КоличествоСтрок=Матрица.Количество();
КоличествоСтолбцов=Матрица[0].Количество();
Решение=Новый Массив(КоличествоСтрок);
// отсортируем матрицу так, чтобы по диагонали располагались наибольшие по модулю значения
Для Стр= 0 По КоличествоСтрок-1 Цикл
//Поиск максимального элемента в столбце
МаксимальныйЭлементСтолбца=Матрица[Стр][Стр];
НомерСтрокиМаксЭлемента=Стр;
Для ПодСтр=СтрПоКоличествоСтрок-1 Цикл
Если МодульЧисла(Матрица[ПодСтр][Стр])>МодульЧисла(МаксимальныйЭлементСтолбца) Тогда
МаксимальныйЭлементСтолбца=Матрица[ПодСтр][Стр];
НомерСтрокиМаксЭлемента=ПодСтр;
КонецЕсли;
КонецЦикла;
//Система не разрешима если максимальный элемент равен нулю
Если МаксимальныйЭлементСтолбца= 0 Тогда
Возврат Неопределено;
КонецЕсли;
//Меняем текущую строку со строкой с максимальным элементом
Если НомерСтрокиМаксЭлемента<>Стр Тогда
Для Стб= 0 По КоличествоСтолбцов-1 Цикл
Буфер=Матрица[Стр][Стб];
Матрица[Стр][Стб]=Матрица[НомерСтрокиМаксЭлемента][Стб];
Матрица[НомерСтрокиМаксЭлемента][Стб]=Буфер;
КонецЦикла;
КонецЕсли;
КонецЦикла;
// например, матрица стала такой:
// x1 x2 x3 x4 Св Чл
// -120 0 0 20 -1600 // уравнение для х1
// 20 -170 0 0 -2300 // уравнение для х2
// 0 40 -160 0 -2600 // уравнение для х3
// 0 0 50 -140 -3100 // уравнение для х4
//Разрешим каждое уравнение относительно Хn
Для Стр= 0 поКоличествоСтрок- 1 Цикл
// Меняем местами коэффициент аргумента Хn и свободный член, одновременно меняя знак.
// Как при перестановке члена уравнения за знак "="
Буфер=-Матрица[Стр][Стр];
Матрица[Стр][Стр]=-Матрица[Стр][КоличествоСтолбцов-1];
Матрица[Стр][КоличествоСтолбцов-1]=Буфер;
// разделим строку на коэффициент аргумента Хn, т.е на значение в буфере
Для Кол= 0 поКоличествоСтолбцов- 1 Цикл
Матрица[Стр][Кол]=Матрица[Стр][Кол]/Буфер;
КонецЦикла;
КонецЦикла;
// Матрица из примера примет вид:
// x1 x2 x3 x4 Св Чл
// 13,333 0 0 0,167 1 // уравнение для х1
// 0,118 13,529 0 0 1 // уравнение для х2
// 0 0,727 47,273 -1,909 1 // уравнение для х3
// 0 0 0,357 22,143 1 // уравнение для х4
/ колонки: от 0 до КоличествоСтрок матрицы - для значений вычисленных Х
// колонки: + КоличествоСтрок матрицы - для значений погрешностей П
// еще одна колонка для мычисления максимального значения погрешности в строке
МассивРешений=НовыйМассив();
// добавим нулевое решение
СтрокаРешения=Новый Массив(КоличествоСтрок+КоличествоСтрок+ 1);
Для Инд= 0 поСтрокаРешения.ВГраница() Цикл
СтрокаРешения[Инд]= 0;
КонецЦикла;
МассивРешений.Добавить(СтрокаРешения);
ВсегоРешений=МассивРешений.Количество();
РешениеЕсть=Ложь;
Пока не РешениеЕсть Цикл
ПредыдущееРешение=МассивРешений[ВсегоРешений-1];
// добавим новую строку решения
СтрокаРешения=Новый Массив(КоличествоСтрок+КоличествоСтрок+ 1);
СтрокаПогрещностей="";
Для Инд= 0 поКоличествоСтолбцов- 2 Цикл
// найдем уравнение матрицы, соответствующее решаемому аргументу Х
УравнениеМатрицы=Матрица[Инд];
РешениеХ= 0;
//Обойдем все колонки уравнения и сложим, перемножив на значения Х из предыдущего решения
Для Кол= 0 поКоличествоСтолбцов- 2 Цикл
Если Кол=Инд Тогда
РешениеХ=РешениеХ+УравнениеМатрицы[Кол];
Иначе
РешениеХ=РешениеХ+УравнениеМатрицы[Кол]*ПредыдущееРешение[Кол];
КонецЕсли;
КонецЦикла;
СтрокаРешения[Инд]=РешениеХ;
// рассчитаем когрешности
ИндПогрешности=КоличествоСтолбцов-1 +Инд;
СтрокаРешения[ИндПогрешности]=РешениеХ-ПредыдущееРешение[Инд];
СтрокаПогрещностей=СтрокаПогрещностей+Строка(Формат(СтрокаРешения[ИндПогрешности],"ЧРД=.; ЧГ=0"))+",";
КонецЦикла;
// добавим решение в массив решений
МассивРешений.Добавить(СтрокаРешения);
ВсегоРешений=ВсегоРешений+ 1;
// определим, найдено ли решение
СтрокаПогрещностей=СтрокаПогрещностей+"0";
ПогрешностьРешения= 0;
Выполнить("ПогрешностьРешения = Макс("+СтрокаПогрещностей+");");
Если ПогрешностьРешения= 0 Тогда
Прервать;
КонецЕсли;
СтрокаРешения[КоличествоСтрок+КоличествоСтрок]=ПогрешностьРешения;
РешениеЕсть=ПогрешностьРешения<Точность;
КонецЦикла;
КоличествоИтераций=ВсегоРешений- 1;// исключили нулевое решение
Для Стр= 0 поКоличествоСтолбцов-2 Цикл
Решение[Стр]=СтрокаРешения[Стр];
КонецЦикла;
Возврат Решение;
КонецФункции// РешитьМетодомИтераций()
Сравним решения СЛАУ
| Склад | Метод Гаусса | Метод простых итераций |
| А | 18,2243072606 | 18,2243072542 |
| Б | 15,6734479130 | 15,6734479099 |
| В | 20,1683619783 | 20,1683619754 |
| Г | 29,3458435637 | 29,3458435562 |
Как видно из результатов вычислений разными методами, решения расходятся, начиная с 7 знака после запятой. В контексте решаемой задачи 6 знаков после запятой будет более чем достаточно.
4. Подставляем в таблицу движений полученные значения.
На последнем шаге решения задачи умножим количества операций на рассчитанные «суммы ТР на единицу» и получим сумму движений.
| № | Период | Операция | Склад | Корр склад | Количество приход | Количество расход | Сумма ТР приход | Сумма ТР расход |
| 1 | 01.07.2014 | Сальдо | А | 100 | 1000 | |||
| 2 | 01.07.2014 | Сальдо | Б | 150 | 1500 | |||
| 3 | 01.07.2014 | Сальдо | В | 120 | 1600 | |||
| 4 | 01.07.2014 | Сальдо | Г | 90 | 1900 | |||
| 5 | 05.07.2014 | Перемещение | Б | А | 20 | 1164,49 | ||
| 6 | 05.07.2014 | Перемещение | А | 20 | 364,49 | |||
| 7 | 10.07.2014 | Перемещение | В | Б | 40 | 1626,94 | ||
| 8 | 10.07.2014 | Перемещение | Б | 40 | 626,94 | |||
| 9 | 11.07.2014 | Комплектация | Г | 60 | 1760,75 | |||
| 10 | 12.07.2014 | Перемещение | Г | В | 50 | 2208,42 | ||
| 11 | 12.07.2014 | Перемещение | В | 50 | 1008,42 | |||
| 12 | 13.07.2014 | Комплектация | Г | 40 | 1173,83 | |||
| 13 | 16.07.2014 | Перемещение | А | Г | 20 | 1186,92 | ||
| 14 | 16.07.2014 | Перемещение | Г | 20 | 586,92 | |||
| 15 | 17.07.2014 | Переработка | В | 15 | 302,53 | |||
| 16 | 18.07.2014 | Переработка | В | 20 | 403,37 | |||
| 17 | 20.07.2014 | Реализация | А | 100 | 1822,43 | |||
| 18 | 25.07.2014 | Реализация | Б | 130 | 2037,55 | |||
| 19 | 31.07.2014 | Сальдо | А | 0 | 0 | |||
| 20 | 31.07.2014 | Сальдо | Б | 0 | 0 | |||
| 21 | 31.07.2014 | Сальдо | В | 105 | 2117,68 | |||
| 22 | 31.07.2014 | Сальдо | Г | 140 | 4108,42 |
Задача решена
Во вложении обработка, в которой я реализовал сравнение двух методов решения СЛАУ на примере массива 4 х 5
Полезные ссылки
Благодарности.
Sitkovskiy Konstantin - за функцию решения СЛАУ по методу Гаусса


