Доброго времени суток, коллеги. Сегодняшняя статья посвящена генетическому алгоритму. Тема это довольно модная и широко известная, но в практике 1С-нега довольно редко применимая. Утомлять Вас долгими подробностями и историей создания я не хочу – по теме много материала, и Вы легко найдете ответы на все самые общие вопросы. Попытаюсь кратко изложить суть и принцип работы алгоритма, так как реализую его сам максимально коротко и, надеюсь, общедоступно.
Итак, есть некая задача, решение которой состоит из конечного набора переменных. В терминах генетики такое решение называется геномом. Как и в природе, геном обычного организма состоит из конечного числа генов и полностью описывает генотип. То есть организм с полным и валидным генотипом отвечает всем признакам своего биологического вида и может размножаться с представителями своего вида и участвовать в увлекательной борьбе за существование. Некоторое конечное число организмов одного вида, представляющих различные варианты геномов, образуют популяцию. А в терминах задачи популяция есть не конечное (случайное или опорное) множество возможных решений.
После формирования начальной популяции генетический алгоритм имитирует эволюцию, приводя нас к образованию наиболее приспособленного к окружающей среде (критерию оптимизации) генотипа. Оценка приспособленности организма описывается целевой функцией, которая может быть рассчитана для любого экземпляра популяции. После проведения оценки приспособленности наших особей (решений) мы начинаем их комбинировать через размножение.
Циклический этап генетического алгоритма называется поколением, по аналогии, очевидно, с эволюционным процессом. На поколение отводится определенное число размножений, и далеко не всем особям повезет в этом процессе поучаствовать. Вероятность размножения - произвольная функция от оценки приспособленности особи к условиям среды (значения целевой функции), а следовательно, больше потомства дадут наиболее приспособленные особи. Само размножение в информатике не столь интересно, как в природе. Гены (переменные) двух подходящих на размножение кандидатов перемешиваются случайным образом, чтобы их потомок обладал частями решения от каждого из родителей. Нет ни мамы, ни папы, нет детства и отрочества. Есть просто новая особь популяции, готовая приступить к борьбе за существование прямо со следующего поколения.
Когда количество возможных размножений достигнуто и родилось ровно назначенное количество детей, популяцию нужно сократить. Процесс очень простой - сортируем особи по целевой функции и всех лишних ... теряем. Без похорон и салютов.
Дальше при необходимости можно устроить нашим особям мутацию - то есть взять случайное число случайных генов (переменных) у случайных особей и инициировать их заново случайными значениями. Интенсивность мутаций - также один из параметров алгоритма.
Вот, собственно, и все. Поколение за поколением идет наш неестественный отбор, пока наконец не будет достигнут предел поколений или не наступит генетическое однообразие - то есть размножение как таковое потеряет смысл ввиду одинаковости генотипов родителей. Такую популяцию можно еще до бесконечности встряхивать мутациями, но в общем-то очевидно, что предел генетического совершенства достигнут и можно брать первый понравившийся Вам организм в качестве готового решения. Поэтому в генетическом алгоритме есть критерий сходимости для остановки алгоритма - доля одинаковых особей в популяции, который имеет смысл применять при наличии мутаций, чтобы не ждать решения до истечения всех отведенных параметрами поколений. В случае же отсутствия мутаций сходимость также имеет смысл, но именно в этом случае она на практике может достичь 1. То есть мы заполним всю популяцию клонами.
Теперь сформулирую этапы работы алгоритма:
1. Формирование случайной начальной популяции возможных решений.
2. Оценка "приспособленности особей" - вычисление целевой функции.
3. Оценка вероятностей размножения в популяции.
4. Размножение путем случайной рекомбинации частей геномов двух особей. Количество размножений фиксировано параметром поиска решения. Вероятность участия в размножении особи тем больше, чем ближе значение целевой функции к оптимальному.
5. Рассчитываем целевые функции для вновь рожденных особей.
6. Уменьшаем размер популяции до заданного сортировкой по значению целевой функции и отсечением "лишних", наименее приспособленных.
7. Проверяем сходимость решения и количество поколений. Если условие прекращения алгоритма достигнуто - выход и возврат лучшей "особи". Если нет - переход к следующему шагу.
8. Если необходимо по параметрам решения - проводим мутации, изменяя случайное количество генов в случайном количестве особей на случайные значения из ОДЗ. Вычисляем целевые функции для мутировавших особей.
9. Возврат к шагу 3.
Теперь об области применения и относительной эффективности алгоритма. Классически считается, что генетический алгоритм является альтернативой традиционным методам поиска решения и используется там, где есть большие проблемы в формализации задачи и условий оптимизации, большие неровности и разрывы в целевой функции и т.д. Действительно, при не дифференцируемой целевой функции применить традиционный метод градиентного спуска не представляется возможным. Аналогичные проблемы возникают и при множестве локальных минимумов целевой функции - чтобы выбраться из минимума и охватить всю область решения как можно шире, применение популяции, случайных рекомбинаций и мутаций намного более эффективно.
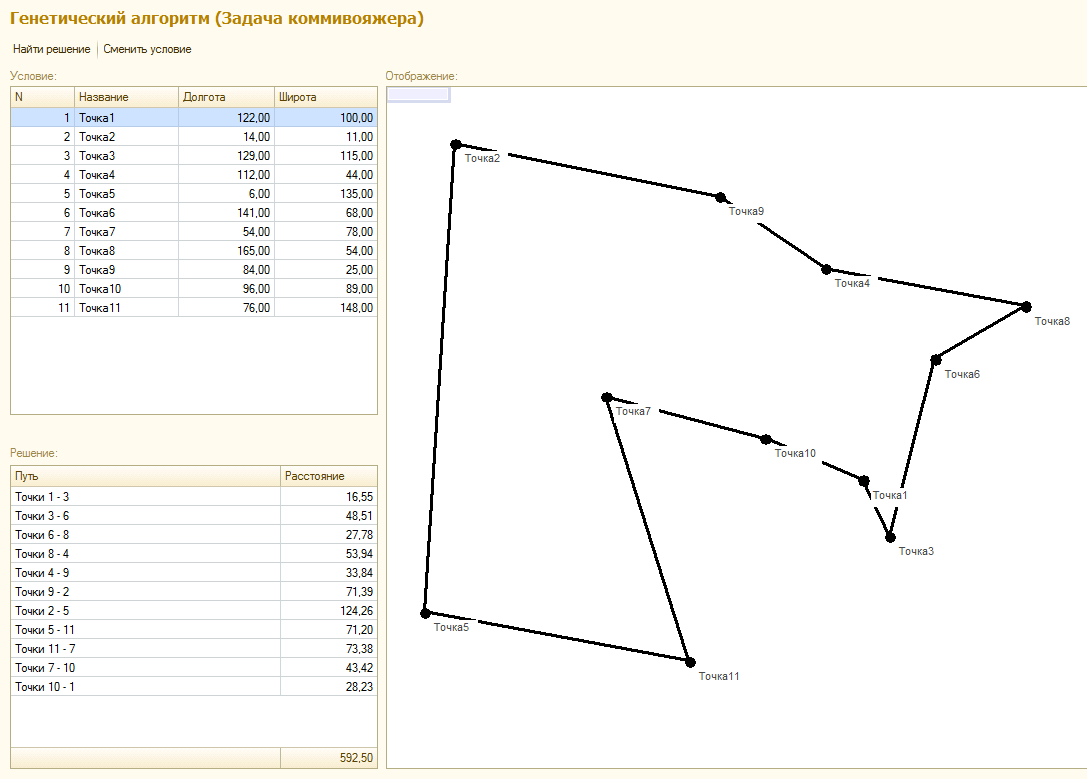
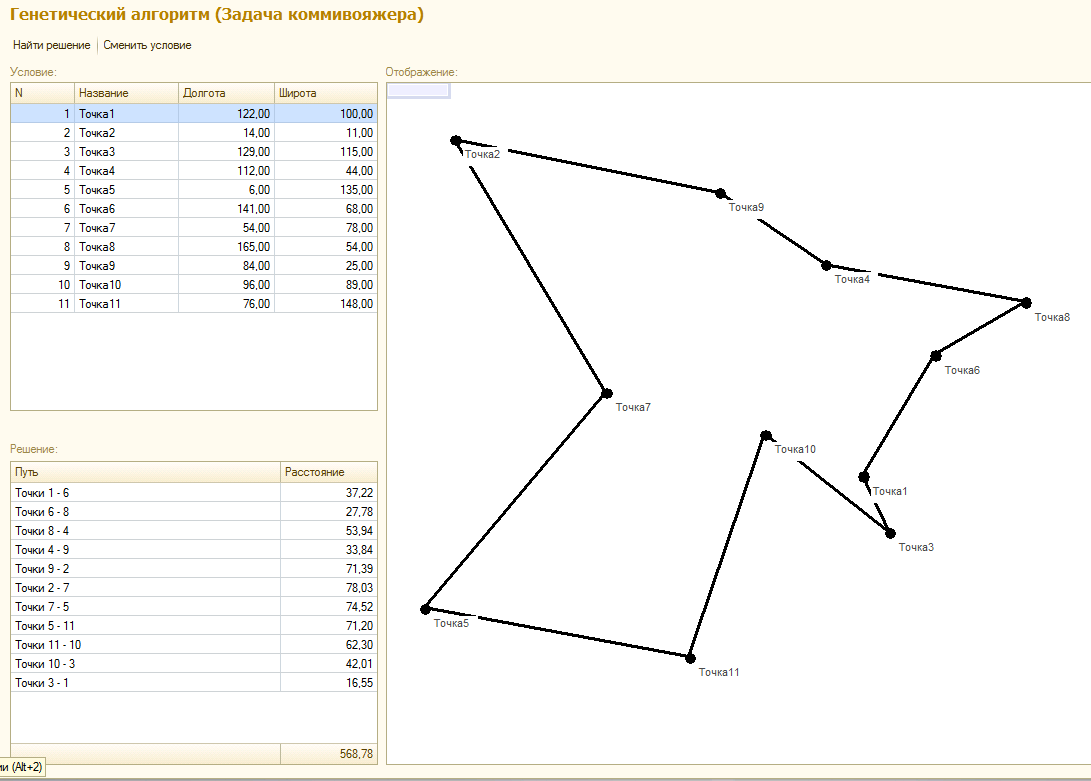
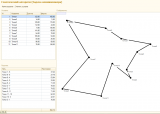
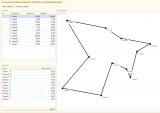
Лично я применяю генетический алгоритм там, где ОДЗ переменных выражено дискретными рядами чисел и целевая функция имеет прерывистый характер. Классический пример - задача коммивояжера. Решение всегда состоит из одинакового числа ребер графа, по которым должен пройти коммивояжер, а набор возможных маршрутов для каждого этапа пути (переменной) ограничен возможными вершинами графа, еще не посещенными на предыдущих шагах. Целевая же функция (затраты на передвижение), очевидно, также дискретна, так как состоит из возможных оценок возможных путей коммивояжера, а не определена непрерывно на каком-либо отрезке. В таком случае ее невозможно продифференцировать и нет функциональных критериев спуска в минимум.
В общем-то, главное достоинство генетического алгоритма в том, что он всегда найдет какое-нибудь решение, и мы можем быть уверены, что это решение лучшее из многих возможных. И применим он для любых задач и любых видов целевой функции. Однако качество самого решения, скажу честно, далеко от идеала. Это скорее способ получить решение произвольной задачи в условиях ограниченного времени, чем добиться идеальной производительности системы.
Впрочем, Вы и сами можете легко убедиться в этом на предложенном демо примере. Для одной и той же системы вершин задачи коммивояжера алгоритм может выдать в разных попытках разные решения. Решения не плохие, но и не идеальные, а разрыв в целевой функции между лучшим и худшим вариантами может достигать 10%.
Функция для поиска решения в приложенной обработке, как обычно универсальна. Можете копипастить и пользоваться. Описание аргументов в комментах к функции. Ну и пример решения!:)
Теперь использованная литература и что вообще почитать:
Т.В. Панченко "Генетические алгоритмы". Издательский дом «Астраханский университет» 2007
Предложения, замечания, пожелания и критику прошу, как обычно, в комментарии.
Вступайте в нашу телеграмм-группу Инфостарт