Задача нахождения наибольшей общей подпоследовательности (англ. longest common subsequence, LCS) — задача поиска последовательности, которая является подпоследовательностью нескольких последовательностей (обычно двух). Статья на вики (Пример взят оттуда)
Один из вариантов получения степени схожести двух строк.
Подпоследовательность отличается от подстроки. Например, если есть исходная последовательность "ABCDEF", то "ACE" будет подпоследовательностью, но не подстрокой.
Используется метод динамического программирования.
Функция НаибольшаяОбщаяПоследовательность(Стр1, Стр2)
МСтр1 = МассивИзСтроки(Стр1);
МСтр2 = МассивИзСтроки(Стр2);
м = МСтр1.Количество();
н = МСтр2.Количество();
Т = Новый ТаблицаЗначений;
Для ит = 0 По н Цикл
Т.Колонки.Добавить("К" + ит);
КонецЦикла;
Для ит = 0 По м Цикл
НовСтр = Т.Добавить();
КонецЦикла;
Т.ЗаполнитьЗначения(0);
Для итС = 1 По м Цикл
Для итК = 1 По н Цикл
Если МСтр1[итС-1] = МСтр2[итК-1] Тогда
Т[итС][итК] = Т[итС-1][итК-1] + 1;
Иначе
Т[итС][итК] = Макс(Т[итС][итК-1], Т[итС-1][итК]);
КонецЕсли;
КонецЦикла;
КонецЦикла;
Возврат ВывестиНОП(Т, МСтр1, МСтр2, м, н);
КонецФункции
Функция ВывестиНОП(Т, МСтр1, МСтр2, итС, итК)
Если итС = 0 ИЛИ итК = 0 Тогда
Возврат "";
ИначеЕсли МСтр1[итС-1] = МСтр2[итК-1] Тогда
Возврат ВывестиНОП(Т, МСтр1, МСтр2, итС-1, итК-1) + МСтр1[итС-1];
Иначе
Если Т[итС][итК-1] > Т[итС-1][итК] Тогда
Возврат ВывестиНОП(Т, МСтр1, МСтр2, итС, итК-1);
Иначе
Возврат ВывестиНОП(Т, МСтр1, МСтр2, итС-1, итК);
КонецЕсли;
КонецЕсли;
КонецФункции
Функция МассивИзСтроки(ИсходнаяСтрока)
Результат = Новый Массив;
Длина = СтрДлина(ИсходнаяСтрока);
Для ит=1 По Длина Цикл
Результат.Добавить(Сред(ИсходнаяСтрока, ит, 1));
КонецЦикла;
Возврат Результат;
КонецФункции
Получаем таблицу длин наибольших общих полседовательностей (таблица значений Т).
Для строк "DCBA" и "ABCB" таблица выглядит так:
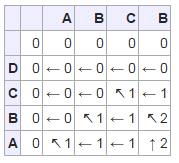
Например пересечение Т[2][3]равно 1. Значит для строк "DC" и "ABC" длина НОП = 1 (подпоследовательность "C").
Для Т[4][4] равно 2 (подпоследвоательность "CB").
Для того, чтобы получить НОП, нужно пройти эту таблицу из нижнего правого угла в левый верхний, поднимаясь по стрелкам.
Как получаются стрелки:
итС - индекс строки таблицы Т
итК - индекс колонки таблицы Т
МСтр1, МСтр2 - массивы символов строки1 и строки2
Если МСтр1[итС-1] = МСтр2[итК-1] - диагональная стрелка, этот элемент входит в НОП. Т[3][4] соответствует 3-му символу строки "DCBA" ("B") и 4-му символу строки "ABCB" ("B") .
Если Т[итС][итК-1] > Т[итС-1][итК] - стрелка влево
Если Т[итС][итК-1] <= Т[итС-1][итК] - стрелка вверх
Поднимаясь из правого нижнего угла мы можем двигаться по диагонали (если символ входит в НОП), либо пропускаем символ в первой строке (стрелка вверх), либо пропускаем символ во второй строке (стрелка влево).
В приложенной обработке только описанная функция.