Получаем формулу.
Экзамен 1С:Профессионал состоит из 14 разных вопросов (случайным образом выбирается по 1 вопросу из 14 тематических разделов). Ответ на один вопрос можно рассмотреть как событие с двумя возможными исходами: ответил неверно (0), ответил верно (1).
Экзамен в этом случае будет представлять собой более сложное событие с бОльшим количеством возможных исходов:
(00000000000000) - на все вопросы ответил неверно,
(00000000000001) - верно ответил только на последний вопрос,
(00000000000010) - верно ответил только не предпоследний вопрос,
...
(11111111111111) - верно ответил на все вопросы.
Однако успешной сдаче экзамена соответствуют только те исходы, где минимум 12 верных ответов, например:
(00111111111111) - верно ответил на все вопросы, кроме первого и второго,
(01011111111111) - верно ответил на все вопросы, кроме первого и третьего,
...
(11111111111110) - верно ответил на все вопросы, кроме последнего,
(11111111111111) - верно ответил на все вопросы.
Наша цель рассчитать вероятность того, что экзамен окончится одним из таких успешных исходов.
Теорема сложения вероятностей несовместных событий: вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
P(A+B) = P(A)+P(B)
Следствие: Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
P(A1+A2+...+An) = P(A1)+P(A2)+...+P(An).
По теореме сложения вероятностей несовместных событий получим, что вероятность успешной сдачи экзамена равна сумме вероятностей всех возможных успешных исходов:
P = P(00111111111111) + P(01011111111111) + … + P(11111111111110) + P(11111111111111).
Осталось понять, как вычислить вероятность каждого успешного исхода.
Теорема умножения вероятностей независимых событий: вероятность совместного появления независимых событий A и B равна произведению вероятностей этих событий:
P(AB) = P(A)*P(B)
Следствие: вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
P(A1A2...An) = P(A1)*P(A2)*...*P(An).
Если вероятность верного ответа на вопрос из раздела N обозначить как pN, а вероятность неверного ответа – qN, то вероятность каждого исхода экзамена можно описать более детально, например:
P(00111111111111) = q1*q2*p3*p4*p5*p6*p7*p8*p9*p10*p11*p12*p13*p14,
P(01011111111111) = q1*p2*q3*p4*p5*p6*p7*p8*p9*p10*p11*p12*p13*p14,
…
P(11111111111110) = p1*p2*p3*p4*p5*p6*p7*p8*p9*p10*p11*p12*p13*q14,
P(11111111111111) = p1*p2*p3*p4*p5*p6*p7*p8*p9*p10*p11*p12*p13*p14.
Чтобы не набирать итоговую длинную формулу вручную, напишем обработку, которая сделает это за нас.
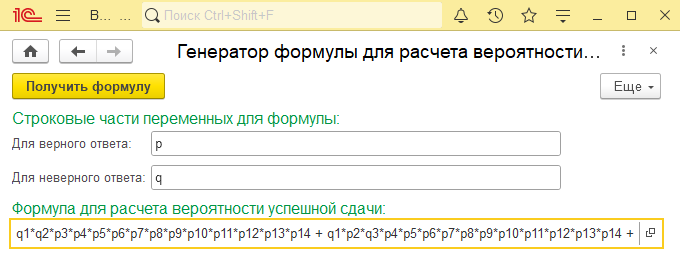
С помощью обработки получаем следующую формулу:
Учтем еще один момент.
Теорема: Сумма вероятностей противоположных событий равна 1:
P(A)+P(¬A) = 1
Так как неверный ответ на вопрос является противоположностью верного ответа, то вероятность неверного ответа на вопрос из раздела 1 можно получить вычитанием вероятности верного ответа из 1, т.е.
q1 = 1-p1.
Всей полученной выше информации достаточно, чтобы сделать простой инструмент для подсчета вероятности.
Оценим шансы сдать экзамен без подготовки.
Представим себе ситуацию, что испытуемый на экзамене отвечает полностью наугад, даже не читая вопросы и ответы. В этом случае вероятность ответа на вопрос будет зависеть от того, сколько вариантов ответа предлагается к выбору. Рассмотрим наиболее удачный вариант – все четырнадцать вопросов попались всего с двумя вариантами ответов. Значит, вероятность верного ответа на каждый вопрос будет 50%.
Если взять ранее полученную формулу подсчета вероятности сдачи экзамена и приложить некоторые усилия, то на выходе получим простой и удобный инструмент для подсчета вероятности в виде таблицы. Вносим в таблицу начальные данные для нашего идеализированного случая:

и получаем итоговую вероятность 0,65%. То есть 0,65% - это максимум, на который стоит рассчитывать при сдаче экзамена наугад.
Стоит попасться одному вопросу, где будет не два варианта ответа, а хотя бы три, то вероятность уже падает до 0,49%.

А если все 14 вопросов будут с тремя вариантами ответов, то вероятность успешной сдачи наугад снижается ниже 0,01%, а точнее 0,000082%.

Стоит напомнить, что в вопросах теста 1С:Профессионал могут попасться вопросы с 4-6 вариантами ответа, такие вопросы также будут уменьшать шансы успешной сдачи. Думаю, этих результатов достаточно для оценки сдачи экзамена наугад. Шанс есть, но он настолько мал, что надеяться на него нерационально.
Оценим шансы сдать экзамен с подготовкой (в общем случае).
Представим себе ситуацию, что испытуемый на любой заранее изученный вопрос отвечает верно, а на любой незнакомый вопрос – неверно (например, невезучий человек с хорошей памятью). Такой человек, изучив половину вопросов из каждого раздела (т.е. вероятность верного ответа у него 50%) может рассчитывать лишь на 0,65% (максимальная вероятность, на которую мог рассчитывать везучий человек без подготовки из примеров выше).
Попробуем сравнить это с другими раскладами.
Например, если испытуемый изучил по 70% вопросов из каждого раздела, то вероятность будет около 16%.

Если изучил по 80% вопросов из каждого раздела, то вероятность уже около 45%.

Ну а если по 90% вопросов, то вероятность 84%.

Самостоятельно можно сравнить и с другими раскладами (инструмент приложен в виде файла "Расчет вероятности для общего случая.xlsx").
Оценим шансы сдать экзамен с подготовкой (в конкретном случае).
С помощью представленного выше инструмента можно сформировать примерное представление об экзамене в целом, но не очень удобно оценивать объем работы, необходимый для подготовки к конкретному экзамену, так как количество вопросов в разделах может сильно отличаться. Попробуем исправить этот недостаток.
Вероятность наступления события A в некотором испытании равна отношению P(A) = m/n, где:
n – общее число всех равновозможных, элементарных исходов данного испытания, которые образуют полную группу событий;
m – количество элементарных исходов, благоприятствующих событию A.
Если количество вопросов в разделе 1 обозначить как n1, а количество изученных вопросов из этого раздела обозначить как m1, то вероятность верного ответа на вопрос из раздела 1 будет равна
p1 = m1/n1.
Используя эту информацию, сделаем другой простой инструмент, где вероятность рассчитывается на основании количества изученных вопросов (на которые ожидается верный ответ) и общего количества вопросов в разделах.
У меня под рукой оказался комплект вопросов на знание основных механизмов платформы 1С:Предприятие (редакция от 2014 года). Если заполнить количество вопросов по разделам и подставить различные исходные данные, то можно получить интересные результаты.
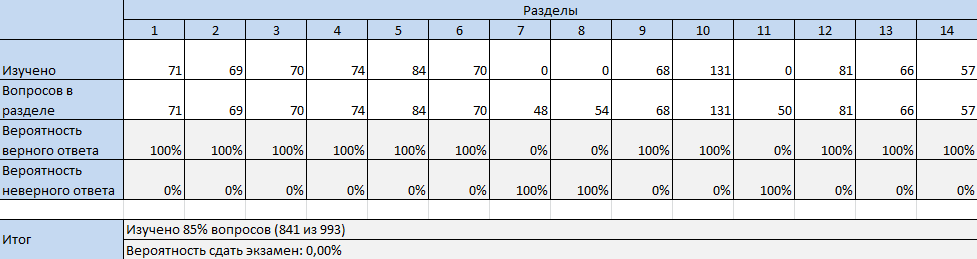
Можно представить себе крайне неудачную подготовку: изучить 85% вопросов, но не иметь шансы на сдачу (вероятность 0%). Человек будет каждый раз набирать только 11 верных ответов на вопросы. Ситуация соответствует случаю, если человек начинает изучать вопросы по разделам (начиная с более крупного), но не успевает разобрать последние 3 самых мелких раздела.
А вот если начать изучать вопросы с мелких разделов, то с меньшего количества - 78% вопросов уже можно получить 100% вероятность успешной сдачи.
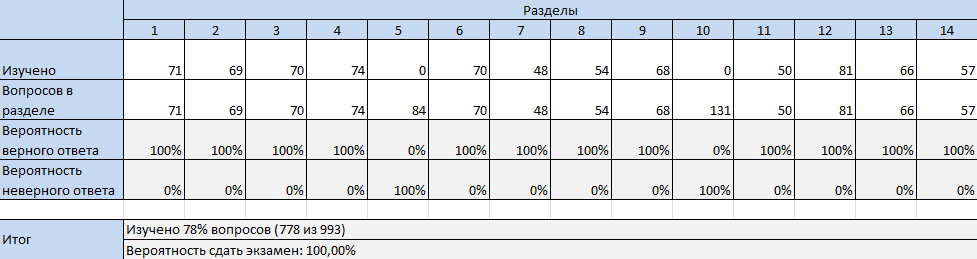
Но стоит изучить на 1 раздел меньше как вероятность снова равна 0.
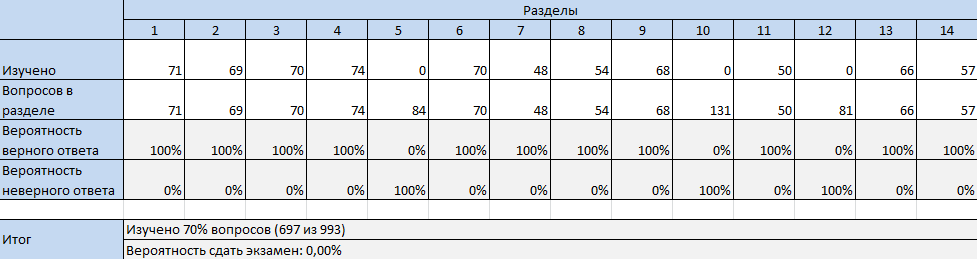
В то же время, если эти же 70% изученных вопросов распределить иначе, то вместо 0% можно получить 28%.
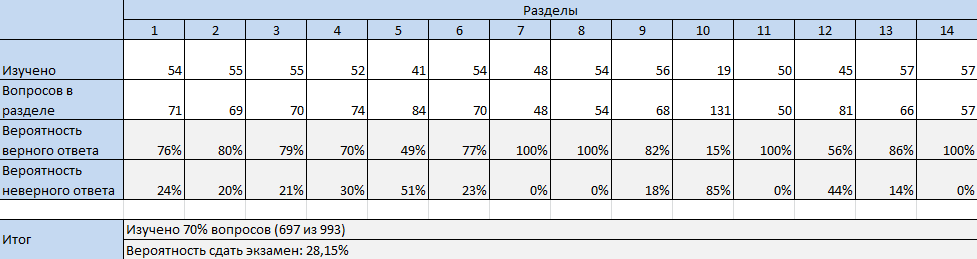
С этим инструментом уже более точно можно оценить объем предстоящей подготовки (инструмент приложен в виде файла "Расчет вероятности для конкретного случая.xlsx").
Однако не стоит забывать, что один и тот же вопрос/раздел для одного человека может показаться простым, а для другого - сложным. Кому-то проще изучить больше вопросов по знакомой теме, чем малое количество вопросов абсолютно незнакомой тематики.
Заключение.
С помощью теории вероятности можно оценить шансы сдачи теста 1С:Профессионал.
Шансы сдать экзамен наугад по абсолютно незнакомой теме настолько мал, что лучше потратить какое-то время на подготовку.
Одинаковое количество изученных вопросов может дать разную вероятность (в зависимости от того, как изученные вопросы распределены по разделам).
Полученные инструменты можно использовать для оценки предстоящего объема работы для подготовки (примерно понять, сколько вопросов нужно изучить для получения приемлемого шанса успешной сдачи).
Upd.
Инструмент с более широким функционалом выложил в публикации: Вероятность сдачи тестирования 1С:Профессионал (расчет, прогноз и визуализация).
Вступайте в нашу телеграмм-группу Инфостарт