Расчет процентной ставки по кредиту/инвестиции (аналог СТАВКА в Excel)

Теоретичекая часть:

Формула СТАВКА в Excel вычисляет процентную ставку по кредиту или инвестиции на основе равномерных периодических платежей. Это одна из ключевых финансовых функций.

Описание алгоритма:

Пс + [Плт * (1 + ((1 + r)^(тип_платежа = 1 ? r : 0)) * ((1 - (1 + r)^(-Кпер)) / r)] + [Бс * (1 + r)^(-Кпер)] = 0

Подробный алгоритм (Итеративный метод)

Прямого алгебраического решения для r в этом уравнении не существует (за исключением некоторых частных случаев). Поэтому Excel использует итеративный численный метод, а именно метод Ньютона-Рафсона или другой подобный метод (например, секущих). Метод Ньютона-Рафсона является наиболее вероятным кандидатом из-за его быстрой сходимости.

Шаг 1: Подготовка и нормализация данных

1. Проверить входные данные. Если Плт = 0, задача тривиальна и решается прямым вычислением.

2. Привести все знаки денежных потоков к единой логике. Обычно принято, что:

   • Исходящие платежи (уплаты) имеют знак "-" (например, Пс - сумма полученного кредита, Плт - регулярный платеж по кредиту).

   • Входящие платежи (поступления) имеют знак "+".

   • Для корректной работы алгоритма знаки Пс и Плт должны быть противоположными.

Шаг 2: Определение Целевой Функции

Преобразуем основное уравнение в целевую функцию f(r), которую мы будем искать ноль (корень).

f(r) = Пс + Плт * [1 + (тип_платежа * r)] * [ (1 - (1 + r)^(-Кпер)) / r ] + Бс * (1 + r)^(-Кпер)

Наша цель — найти такое r, при котором f(r) = 0.

Шаг 3: Выбор Начального Приближения

Методу Ньютона-Рафсона нужно начальное предположение для ставки (r_guess).

• Если аргумент предположение не задан пользователем, Excel, вероятно, использует начальное значение, например, 0.1 (10%).

• Это предположение может быть улучшено на основе анализа денежных потоков.

Шаг 4: Итерационный Процеск (Цикл) Метода Ньютона-Рафсона

На каждой итерации i алгоритм выполняет следующие действия:

1. Вычисление целевой функции: Рассчитывается f(r_i) по формуле выше, используя текущее предположение r_i.

2. Вычисление производной: Рассчитывается производная целевой функции f'(r_i). Производная показывает скорость изменения функции и вычисляется аналитически (это одна из сильных сторон метода Ньютона).

   • Производная f'(r) для этой функции довольно громоздкая, но она вычисляется по правилам дифференцирования.

3. Обновление предположения: Вычисляется новое, более точное значение ставки r_{i+1} по формуле Ньютона-Рафсона:
   r_{i+1} = r_i - f(r_i) / f'(r_i)

4. Проверка условия сходимости: Проверяется, насколько новое значение близко к предыдущему.

   • Если |r_{i+1} - r_i| < ε (где ε - очень маленькое число, например, 1e-7), то необходимая точность достигнута. Алгоритм завершает работу, и r_{i+1} является ответом.

   • Если условие не выполнено, шаги 1-4 повторяются с новым значением r_{i+1}.

Шаг 5: Обработка особых случаев и ошибок

• Сходимость: Если после определенного количества итераций (например, 20-30) решение не найдено, Excel возвращает ошибку #ЧИСЛО!. Это может произойти, если начальное предположение было очень плохим или если решение не существует (например, все платежи положительные).

• Нулевые платежи: Если Плт = 0, уравнение упрощается, и ставка может быть найдена напрямую: r = (Бс / Пс)^(1/Кпер) - 1.

Простой пример для понимания логики

Допустим, вы взяли кредит 100 000 руб. (Пс = -100000) на 12 месяцев (Кпер = 12) и платите по 10 000 руб. в месяц (Плт = 10000). В конце срока остатка нет (Бс = 0). Платежи в конце периода (тип = 0).

Алгоритм будет искать ставку r (месячную), при которой:
-100000 + 10000 * [(1 - (1 + r)^(-12)) / r] = 0

Или:
10000 * [(1 - (1 + r)^(-12)) / r] = 100000

Метод Ньютона-Рафсона будет подбирать r, начиная, скажем, с 5% (0.05), пока не найдет, что значение r ≈ 0.02923 (т.е. ~2.923% в месяц) удовлетворяет уравнению с высокой точностью. Годовая ставка при этом составит 0.02923 * 12 ≈ 35.08%.

Резюме

Алгоритм функции СТАВКА — это классический пример применения итеративного численного метода (скорее всего, метода Ньютона-Рафсона) для решения сложного финансового уравнения, не имеющего простого аналитического решения. Он работает через последовательное приближение, минимизируя ошибку до тех пор, пока не будет достигнута заданная точность.

Листинг кода на языке 1с:

#Область РасчетСтавкиИТестирование

// Вычисляет процентную ставку по кредиту/инвестиции (аналог СТАВКА в Excel)
// 
// Параметры:
//  Кпер          - Общее количество периодов платежей
//  Плт           - Выплата в каждый период
//  Пс            - Текущая стоимость (сумма кредита)
//  Бс            - Будущая стоимость (остаток после последнего платежа)
//  ТипПлатежа    - 0 (конец периода) или 1 (начало периода)
//  Предположение - Начальное предположение о ставке (обычно 0.1)
//  Точность      - Точность вычисления (по умолчанию 0.00000001)
//
// Возвращает:
//  Процентную ставку за период
//
Функция Ставка(Кпер, Плт, Пс, Бс = 0, ТипПлатежа = 0, Предположение = 0.1, Точность = 0.00000001) Экспорт
    
    // Проверка входных данных
    Если Не ЗначениеЗаполнено(Кпер) Или Не ЗначениеЗаполнено(Плт) Или Не ЗначениеЗаполнено(Пс) Тогда
        ВызватьИсключение "Не заполнены обязательные параметры: Кпер, Плт, Пс";
    КонецЕсли;
    
    Если Кпер <= 0 Тогда
        ВызватьИсключение "Кпер должен быть больше 0";
    КонецЕсли;
    
    // Особый случай: нулевые платежи
    Если Плт = 0 Тогда
        Если Пс = 0 Тогда
            ВызватьИсключение "Деление на ноль";
        КонецЕсли;
        Возврат Pow(Бс / Пс, 1 / Кпер) - 1;
    КонецЕсли;
    
    ТекущаяСтавка = Предположение;
    СчетчикИтераций = 0;
    МаксИтераций = 50; // 50
    
    Пока Истина Цикл
        СчетчикИтераций = СчетчикИтераций + 1;
        
        // Вычисляем значение функции и производной
        ЗначениеФункции = ЗначениеФинансовойФункции(ТекущаяСтавка, Кпер, Плт, Пс, Бс, ТипПлатежа);
        ЗначениеПроизводной = ЗначениеПроизводнойФункции(ТекущаяСтавка, Кпер, Плт, Пс, Бс, ТипПлатежа);
        
        // Проверка деления на ноль
        Если ЗначениеПроизводной = 0 Тогда
            // Пробуем другое начальное предположение
            ТекущаяСтавка = ТекущаяСтавка + 0.1;
            Продолжить;
        КонецЕсли;
        
        // Формула Ньютона-Рафсона
        НоваяСтавка = ТекущаяСтавка - ЗначениеФункции / ЗначениеПроизводной;
        
        // Проверяем сходимость (используем Макс() для получения модуля)
        Разница = НоваяСтавка - ТекущаяСтавка;
        МодульРазницы = Макс(Разница, -Разница);
        Если МодульРазницы < Точность Тогда
            // Проверяем, что ставка имеет финансовый смысл
            Если НоваяСтавка >= -1 Тогда
                Возврат НоваяСтавка;
            Иначе
                ВызватьИсключение "Вычисленная ставка не имеет финансового смысла";
            КонецЕсли;
        КонецЕсли;
        
        ТекущаяСтавка = НоваяСтавка;
        
        // Защита от бесконечного цикла
        Если СчетчикИтераций > МаксИтераций Тогда
            ВызватьИсключение "Не удалось вычислить ставку за " + МаксИтераций + " итераций. Текущая точность: " + Формат(МодульРазницы, "ЧГ=0");
        КонецЕсли;
        
    КонецЦикла;
    
КонецФункции

// Вычисляет значение финансовой функции f(r)
Функция ЗначениеФинансовойФункции(Ставка, Кпер, Плт, Пс, Бс, ТипПлатежа)
    
    Если Ставка = 0 Тогда
        // Частный случай: нулевая ставка
        Возврат Пс + Плт * Кпер + Бс;
    КонецЕсли;
    
    КоэффициентАннуитета = (1 - Pow(1 + Ставка, -Кпер)) / Ставка;
    
    // Корректировка для платежей в начале периода
    Если ТипПлатежа = 1 Тогда
        КоэффициентАннуитета = КоэффициентАннуитета * (1 + Ставка);
    КонецЕсли;
    
    Возврат Пс + Плт * КоэффициентАннуитета + Бс * Pow(1 + Ставка, -Кпер);
    
КонецФункции

// Вычисляет производную финансовой функции f'(r)
Функция ЗначениеПроизводнойФункции(Ставка, Кпер, Плт, Пс, Бс, ТипПлатежа)
    
    // Вычисляем производную методом конечных разностей
    Дельта = 0.00000001;
    Значение1 = ЗначениеФинансовойФункции(Ставка + Дельта, Кпер, Плт, Пс, Бс, ТипПлатежа);
    Значение2 = ЗначениеФинансовойФункции(Ставка - Дельта, Кпер, Плт, Пс, Бс, ТипПлатежа);
    
    Возврат (Значение1 - Значение2) / (2 * Дельта);
    
КонецФункции

// Вспомогательная функция: преобразует периодическую ставку в годовую
Функция ГодоваяСтавка(СтавкаЗаПериод, ПериодовВГоду = 12) Экспорт
	
	Возврат Pow(1 + СтавкаЗаПериод, ПериодовВГоду) - 1;
	
КонецФункции

// Тестирование:

// Пример 1: Кредит 100,000 на 12 месяцев с платежом 10,000
Процедура ПримерВычисленияСтавки()
    
    // Данные кредита
    СуммаКредита = 100000; // Пс
    Платеж		 = -10000; // Плт  
    Срок		 = 12;     // Кпер
    Остаток		 = 0;      // Бс
    Тип			 = 0;      // Платежи в конце периода
    
    // Вычисляем месячную ставку
    МесячнаяСтавка = Ставка(Срок, Платеж, СуммаКредита, Остаток, Тип);
    
    // Преобразуем в годовую
    ГодоваяСтавка = ГодоваяСтавка(МесячнаяСтавка);
    
    Сообщение = 
        "Результаты расчета:
        |Сумма кредита: " + СуммаКредита + "
        |Ежемесячный платеж: " + Платеж + "
        |Срок: " + Срок + " мес.
        |Месячная ставка: " + Формат(МесячнаяСтавка * 100, "ЧДЦ=4") + "%
        |Годовая ставка: " + Формат(ГодоваяСтавка * 100, "ЧДЦ=4") + "%";
    
    Сообщить(Сообщение);
    
КонецПроцедуры

// Пример 2: Инвестиция с регулярными взносами
Процедура ПримерИнвестиции()
    
	НачальнаяИнвестиция	= -100000;  // Исходящий платеж
	ЕжемесячныйВзнос	= -5000;    // Исходящий платеж
	Срок				= 60;       // 5 лет
	БудущаяСтоимость	= 500000;   // Целевая сумма
	
	МесячнаяСтавка = Ставка(Срок, ЕжемесячныйВзнос, НачальнаяИнвестиция, БудущаяСтоимость);
	ГодоваяДоходность = ГодоваяСтавка(МесячнаяСтавка);
	
	Сообщить("Требуемая годовая доходность: " + Формат(ГодоваяДоходность * 100, "ЧДЦ=4") + "%");
    
КонецПроцедуры

#КонецОбласти

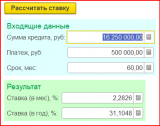
Посмотреть вживую, как работает алгоритм, можно в прикрепленной обработке. Работает на любой конфигурации.