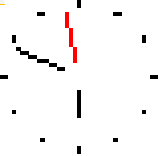
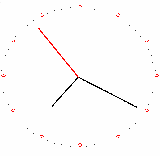
В первую очередь, при запуске обработки подготавливается для отрисовки табличный документ. В связи с тем, что по умолчанию ширина ячейки не равна её высоте, "пиксели" получаются вытянутыми по оси У, в результате чего картинка растягивается. Для того чтобы исправить это, нужно изменить ширину ячеек рабочей области:
Экран.Область("R1C1:R40C40").ШиринаКолонки = 2;
После чего подключается обработчик ожидания с таймингом 0.1
В нём происходит всё самое интересное. Для начала экран очищается, а затем отрисовывается циферблат. Я не буду показывать как это происходит по той причине, что для понимания этого сначала мне стоит объяснить как отрисовываются стрелки. Прежде чем начать отрисовку, необходимо получить текущее время, разбив его на часы, минуты и секунды. После этого полученные данные преобразуются в градусы. Это происходит так:
((ТекущееЗначение-МинимальноеЗначениеИзСтарогоДиапазона) / (МаксимальноеЗначениеИзСтарогоДиапазона-МинимальноеЗначениеИзСтарогоДиапазона)) * (МаксимальноеЗначениеИзНовогоДиапазона-МинимальноеЗначениеИзНовогоДиапазона) + МинимальноеЗначениеИзНовогоДиапазона;
То есть, для минут это выглядит следующим образом:
УголМинутной = Число(Формат(((ТекущаяМинута) / (60)) * (360),"ЧДЦ=; ЧН=0"));
Но для часов всё будет немного интереснее. Если мы просто изменим 60 минут на 12 часов, это будет работать. Однако, на протяжении всего часа маленькая стрелка не сдвинется с места и это будет вызывать затруднения восприятия ближе к концу часа. Поэтому после того как мы проделаем с часами то же что и с минутами, нам нужно будет добавить к полученному количеству градусов значение, полученное из текущего количества минут:
УголЧасовой = УголЧасовой + Число(Формат(((ТекущаяМинута) / (60)) * (30),"ЧДЦ=; ЧН=0"));
Теперь часовая стрелка будет плавно двигаться по кругу в течение всего часа. За это время она пройдёт расстояние, равное пяти минутам для минутной стрелки, а это 30 градусов.
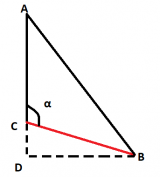
Итак, теперь у нас есть данные об угле наклона каждой стрелки относительно 12 часов и можно приступить к её отрисовке, но как нам найти каждый пиксель стрелки? Для того чтобы вычисление координат стрелок было проще понять, давайте посмотрим на рисунок:
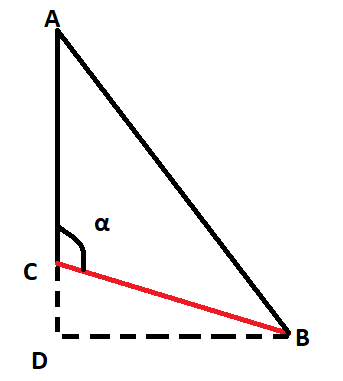
Представим, что все стрелки выходят из точки C. Точка A смотрит ровно на 12 часов, а угол альфа мы только что посчитали. Мы примерно знаем где должна быть наша стрелка CB, но как узнать её координаты? Для себя мы определились, что рисование происходит на поле 40х40 квадратов. Пускай точка С будет иметь координаты 20;20. Длина стрелки пусть будет равняться 16. Теперь мы знаем, что у нас есть равнобедренный треугольник с вершинами в точках 20;20 и 20;4. Длина равных рёбер равна 16, а угол между ними составляет, допустим, 120 градусов. Для того чтобы найти координаты искомой точки B, давайте нарисуем точку D, которая образует прямоугольный треугольник с точками С и B. Школьный курс геометрии говорит, что сторона DB равна sin(180 - α)*BC, а сторона CD эквивалентна cos(180 - α)*BC. Но если сделать эти вычисления, добавить получившиеся длины сторон к центру часов и закрасить полученный пиксель, вместо стрелки будет всего лишь точка. Поэтому рисование происходит в следующей процедуре:
Процедура ВывестиСтрелку(Начало, ДлинаСтрелки, Угол, Цвет)
Если Угол > 180 Тогда
Угол = 360 - Угол;
Вычитание = Истина;
Иначе
Вычитание = Ложь;
КонецЕсли;
Для Счетчик = Начало По ДлинаСтрелки Цикл
КоординатыХ = Число(Формат(20 + Счетчик * Sin((180 - Угол)*(3.1415926535897932/180)) * ?(Вычитание, -1, 1), "ЧДЦ=; ЧН=0"));
КоординатыУ = Число(Формат(20 + Счетчик * Cos((180 - Угол)*(3.1415926535897932/180)), "ЧДЦ=; ЧН=0"));
Экран.Область(КоординатыУ, КоординатыХ).ЦветФона = Цвет;
КонецЦикла;
КонецПроцедуры
Очевидно, что сумма углов треугольника не может превышать 180 градусов, поэтому в начале стоит такая проверка. Не совсем очевидное 3.1415926535897932/180 преобразует наш угол из градусов в радианы, т.к. встроенные функции sin и cos работает только с ними.
После отрисовки обработчик ожидания включается заново в связи с тем, что с интервалами менее 1 секунды он включается однократно. Таким образом получается рекурсивныя процедура рисования, вызывающая сама себя 10 раз в секунду.
Вступайте в нашу телеграмм-группу Инфостарт