Основы компьютерной графики
Предисловие
Сейчас не сложно найти информацию по компьютерной графике. Все уже изложено, описано, и ничего нового в этой статье я не расскажу. Никакого смысла писать статью до недавнего времени не было, пока не появилась статья «Продвинутая графика». Изначально я думал, что автор данной статьи, просто решил не выкладывать теории, а реализовал только практическую часть, на что я и указал в комментариях, что неплохо бы привести ссылку на теорию, и привел примеры тригонометрических преобразований, которые были упущены в статье. На что получил довольно странный ответ, что я оказывается, замкнут в тех знаниях, которые дали мне: школа, институт, самообразование, а для новых знаний я совершенно закрыт. А вот автор не несет на себе столь тяжкий груз знаний и поэтому перед ним открывается мир полный волшебства.
Дальше новатор заявил, что подобное преобразование классическим способом сделать невозможно.
В очередной раз убедился, что дискутировать с подобными личностями бесполезно, все аргументы разбиваются в пропасти отсутствия знаний. Если человек не знаком с тригонометрией, невозможно ему объяснить тригонометрические преобразования.
По ключевым словам «1С, графика» теперь поисковик выдаст столь интересную статью на инфостарте, потом найдется деятель, который напишет статью на другом ресурсе: «1С-ник – не программист, на примере компьютерной графики».
Теория
Все преобразования в данной статье будут рассматриваться в 2-мерной системе координат. Сразу отмечу, что преобразования в 3-мерной системе координат сильно не отличаются. Как правило объекты перемещаются и вращаются. С перемещением в декартовой системе координат все просто - координаты точек изменяются простым и понятным образом. Операция поворот – намного сложнее. Как выполнить преобразование поворот? Вычислить длину вектора, найти текущий угол, добавить угол поворота, получить новые координаты – сложно, но можно упростить.

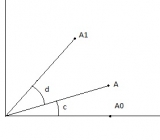
Рассмотрим поворот точки А на угол d. Начальное положение точки рассмотрим, относительно точки А0 - вектор с 0 градусом поворота. Тогда координаты точки A будут равны:
x = x0 * cos(c)
y = x0 * sin(c)
Координаты точки A1 будут равны
x1 = x0 * cos(c + d)
y1 = x0 * sin(c + d)
cos(c + d) = cos (c) * cos(d) - sin(c) * sin(d)
sin(c + d) = sin(c) * cos(d) + sin(d) * cos(c)
x1 = x0 *cos (c) * cos(d) - x0 *sin(c) * sin(d)
x1 = x * cos (d) – y * sin(d)
y1 = x0 * sin(c) * cos(d) + x0 * sin(d) * cos(c)
y1 = y * cos(d) + x * sin(d)
Получившиеся выражения мы можем представить в виде произведения матриц
Надеюсь в этом месте многим в голову пришел вопрос: «Зачем приводить к произведению матриц?».
Дело в том что у произведения матриц есть свойство ассоциативности, которое выглядит следующим образом A * B * C = A * (B * C). Всего-то порядок действий изменился, но это свойство окажется очень полезным в компьютерной графике, к нему вернемся позже.
Как уже многие догадались, все преобразования мы будем приводить к произведению матриц, с поворотом уже все ясно, как же выполнять остальные преобразования, например, перемещение.
Делается это следующим образом – матрицу точек будем задавать тремя значениями (x, y, 1).
Теперь матрица поворота будет выглядеть следующим образом
Матрица перемещения
Где Tx, Ty смещение по x и y.
Матрица масштабирования
Это далеко не весь перечень возможных преобразований, но на этом остановимся, дальше будем рассматривать на примерах.
Примеры графических преобразований
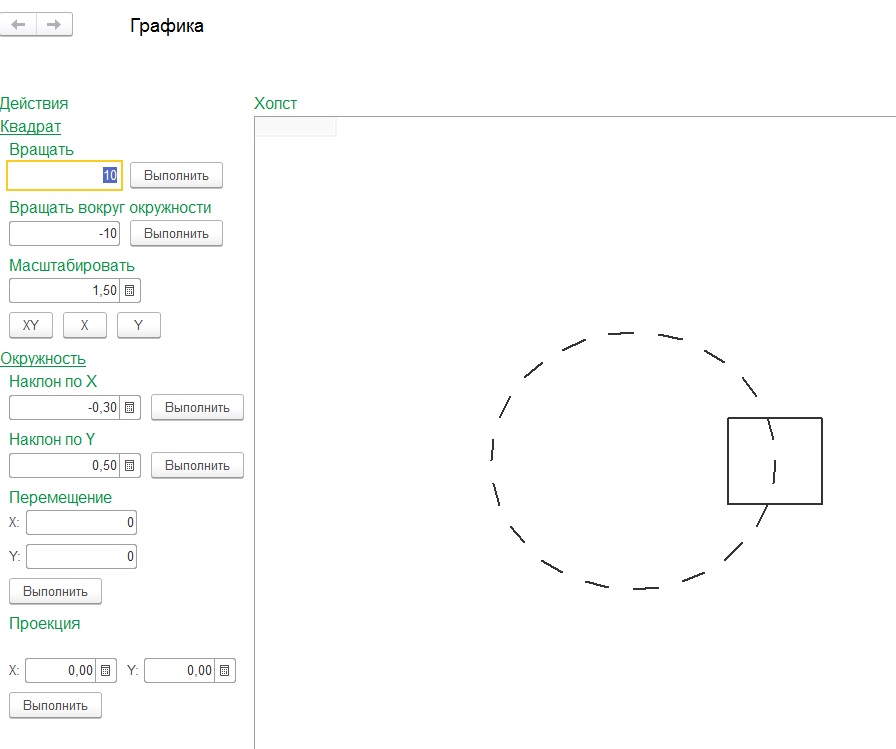
Для демонстрации примеров работы с графикой, я создал обработку в управляемом интерфейсе «графика.epf».
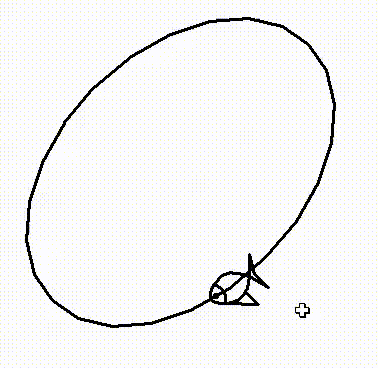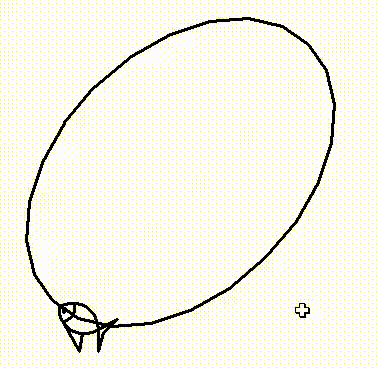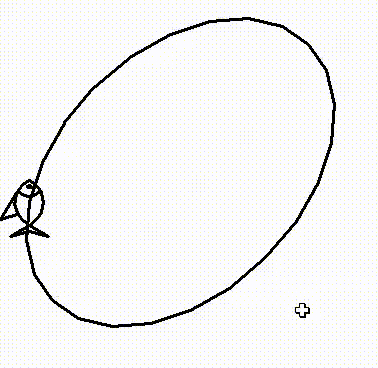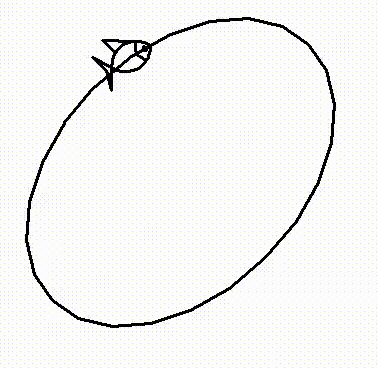
Работать мы будем всего с двумя объектами: окружность и квадрат. Каждый из объектов состоит из прямых линий, линии - состоят из координат концов.
Начало координат я сместил примерно в центр, т.е. окружность расположена в начале координат.
Над квадратом мы будем выполнять следующие преобразования:
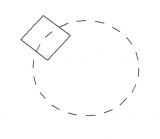
- Вращение вокруг центра квадрата.
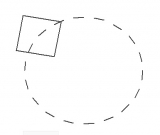
- Вращение вокруг центра окружности.
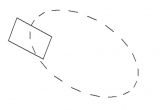
Начальное положение квадрата – смещение по X на радиус сферы. Т.е. чтобы получить координаты нужно матрицу М каждой точки, умножить на матрицу преобразования – перемещения T1.
Теперь, допустим мы хотим повращать квадрат вокруг его центра, делать мы это будем следующим образом: сначала переместим квадрат M * T1, затем умножим на матрицу поворота R2

Теперь повернем квадрат относительно своего центра. Т.е. теперь мы должны матрицу М умножить на матрицу поворота R3
Затем умножить на матрицу перемещения T1, а потом снова на матрицу поворота R2.
Запишем в другой форме – матрицы преобразования вращения квадрата вокруг центра обозначим K с индексом, вокруг окружности O, а также перемещение квадрата на радиус окружности P.
Тогда преобразования примут вид:
M * K1 * K2 * … * KN * P * O1 * O2 * … ON
воспользуемся свойством ассоциативности
M * (K1 * K2 * … * KN) * (P * O1 * O2 * … ON)
т.е. нам не нужно хранить и каждый раз перемножить все матрицы преобразований, достаточно хранить матрицы преобразований на каждом этапе перехода к новой системе исчисления.
Для квадрата таковых три:
- Вращение вокруг собственного центра (а также масштабирование);
- Вращение по радиусу окружности;
- Перемещение окружности (а также другие преобразования).
Другие преобразования - это, например, проецирование.
Не знаю где в двухмерной графике может применяться проецирование, но выглядит эффектно, преобразование работает и на окружность, и на квадрат.
Зато в трехмерной графике проецирование – вещь очень важная. Дело в том угол человеческого зрения – не прямой, а как раз мы видим проекцию, т.е. чем дальше от нас предмет, тем он меньше, подобным образом трехмерное изображение проецируется на плоскость монитора.
После умножения матрицы координат точки на матрицу проецирования – изменится третье значение матрицы координат, которое обычно равняется 1. В данном случае, третье значение будет отличаться от 1, матрица координат примет вид (x, y, s). Что делать с третьим значением? Нужно каждую координату умножить на полученный коэффициент s.
Трехмерная графика
Если статья окажется интересной для посетителей Инфостарта, в следующей статье напишу про основы трехмерной графики, там тоже есть интересные моменты.
Тестирование проводилось на программных файлах 8.3.12.1529.
Вступайте в нашу телеграмм-группу Инфостарт