Данное объявление однажды появилось на станциях минского метро. С его помощью разработчик программного обеспечения искал кандидатов на открывшуюся вакансию. Попробуем решить предложенную задачу.
Разложение числа миллион на простые множители записывается в виде: 1 000 000 =(2^6)*(5^6)
Таким образом, для ответа на поставленный вопрос нам надо найти количество разложений числа 2^6 на шесть множителей, количество разложений числа 5^6 на шесть множителей (заметим, что количества для обоих случаев будут одинаковые) . Перемножить полученные числа и ... еще раз перечитать условие задачи, обратив внимание на выражение "... ЦЕЛЫХ множителей". И так, найдем количество разложений числа 2^6. Эта задача аналогична задаче определения числа размещений 6 одинаковых предметов в шести коробках. Одно из решений следующее. Возьмем 6+5=11 одинаковых предметов. Выберем из них 5. Предметы, которые находятся левее первого выбранного, поместим в первый ящик, предметы которые находятся между первым и вторым - во второй, между вторым и третьим - в третий и т.д. Предметы, которые находятся правее пятого выбранного будут относится к шестому ящику. Количество таких размещений определяется формулой:
Таким образом, искомое количество разложений на натуральные (положительные) множители числа 1 000 000 равно 462². Теперь учтем условие, что возможны отрицательные коэффициенты разложения. Таких коэффициентов может быть либо 2, либо 4, либо 6. Количество подобных разложений равно числу сочетаний из 6 по 2, по 4 и по 6, что равно 15,15 и 1, соответственно. То есть, на каждое найденное разложение будет приходится еще 31 разложение с отрицательными сомножителями. А общее число вариантов составит 462²*32.
Постараемся получить аналогичный результат средствами 1С. А именно, получим размещения 6 двоек по 6 ячейкам. Воспользуемся объектом типа Таблица значений, который содержит колонки с именами Кол0,Кол1,Кол2...Кол5. Для одной двойки и одной ячейки количество размещений равно единице. Это будет таблица с одной колонкой и одной строкой. Следующий шаг - добавить новую ячейку. Мы можем разместить её перед существующими ячейками или расположить за последней. В новую ячейку запишем значение 1.
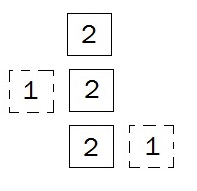
Теперь добавим двойку в получившийся набор ячеек. Добавление (умножение содержимого ячейки) надо провести для каждой клетки в наборе. При этом исходная строка "расщепится" на N строк (где N - это количество ячеек в строке).
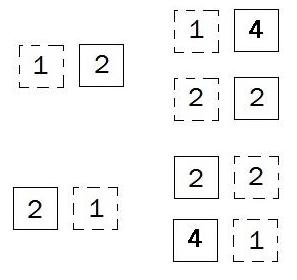
Этот набор содержит повторяющиеся размещения, которые мы уберем с помощью метода Свернуть() объекта ТаблицаЗначений. Повторив изложенную процедуру необходимое число раз, мы получим искомую последовательность. Ниже приводится текст соответствующей процедуры.
Функция ПолучитьСочетания(вхТЗ) экспорт
тЧисло=новый ОписаниеТипов("Число",,,новый КвалификаторыЧисла(10,0));
буфер=вхТЗ.СкопироватьКолонки();
вхРазмер=вхТЗ.Колонки.Количество()-1;
выхРазмер=вхРазмер+1;
буфер.Колонки.Добавить("Кол"+строка(выхРазмер),тЧисло);
Измерение="Кол0";
для н=1 по выхРазмер цикл
Измерение=Измерение+",Кол"+строка(н);
конеццикла;
для каждого стр из вхТЗ цикл
для н=0 по выхРазмер цикл
нСтр=буфер.Добавить();
нСтр[н]=1;
для кол=0 по вхРазмер цикл
если кол<н тогда
нСтр[кол]=стр[кол];
иначе
нСтр[кол+1]=стр[кол];
конецесли;
конеццикла;
конеццикла;
конеццикла;
буфер.Свернуть(Измерение);
выхТЗ=буфер.СкопироватьКолонки();
для каждого запись из буфер цикл
для кол=0 по выхРазмер цикл
нСтр=выхТЗ.Добавить();
ЗаполнитьЗначенияСвойств(нСтр,запись);
нСтр[кол]=нСтр[кол]*2;
конеццикла;
конеццикла;
выхТЗ.Свернуть(Измерение);
возврат выхТЗ;
КонецФункции
Обработка содержит изложенный алгоритм и процедуру контрольного расчета количества размещений с помощью метода динамического программирования.
