Подробное изложение теоретической части алгоритмов и численного интегрирования вообще, можно найти практически в любой книге о численных методах, например - Е. А. Волков "Численные методы", ну или в Википедии -"https://ru.wikipedia.org/wiki/Численное_интегрирование". Особое внимание нужно уделить вопросам выбора узлов и шага интегрирования, обеспечения требуемой точности вычислений, а также применимости и целесообразности выбора того или другого метода.
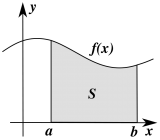
В качестве подинегральной функции рассмотрим "обычную" гладкую и непрерывную функцию (одного аргумента):
Функция Функция_1(х)
Возврат х*х;
КонецФункции
Так будет выглядеть вызов расчетных функций:
Процедура ВыполнитьРасчет()
Число_шагов = 100;
Х_нач = 0;
Х_кон = 5;
Сообщить("Метод левых прямоугольников = " + РассчитатьЛевымиПрямоугольниками(Х_нач, Х_кон, Число_шагов));
Сообщить("Метод правых прямоугольников = " + РассчитатьПравымиПрямоугольниками(Х_нач, Х_кон, Число_шагов));
Сообщить("Метод средних прямоугольников = " + РассчитатьСреднимиПрямоугольниками(Х_нач, Х_кон, Число_шагов));
Сообщить("Метод трапеций = " + РассчитатьТрапециями(Х_нач, Х_кон, Число_шагов));
Сообщить("Метод Симпсона = " + РассчитатьСимпсона(Х_нач, Х_кон, Число_шагов));
КонецПроцедуры
Таким образом, функция F(x)=x^2 интегрируется на интервале от Х_нач до Х_кон, число шагов фиксировано и равно 100 (вообще, для различных методов с целью обеспечения требуемой точности можно рассчитать минимально необходимое число шагов, но для наших ознакомительных целей берем именно фиксированное значение).
Важно также помнить, что при расчетах могут получаться числа с длинной дробной частью, работа с которыми занимает у 1С много времени и сильно тормозит вычисления. Поэтому, например, при определении функции имеет смысл вместо "Возврат F(X)" писать "Возврат Окр(F(X), 16)".
1) Метод левых прямоугольников:
Функция РассчитатьЛевымиПрямоугольниками(Х_нач, Х_кон, Число_шагов)
Сумма = 0;
h = (Х_кон-Х_нач)/Число_шагов;
х = Х_нач;
Для й=0 По Число_шагов-1 Цикл
Сумма = Сумма + h*Функция_1(х);
х = (х + h);
КонецЦикла;
Возврат Сумма;
КонецФункции
2) Метод правых прямоугольников:
Функция РассчитатьПравымиПрямоугольниками(Х_нач, Х_кон, Число_шагов)
Сумма = 0;
h = (Х_кон-Х_нач)/Число_шагов;
х = Х_кон;
Для й=1 По Число_шагов Цикл
Сумма = Сумма + h*Функция_1(х);
х = (х - h);
КонецЦикла;
Возврат Сумма;
КонецФункции
3) Метод средних прямоугольников:
Функция РассчитатьСреднимиПрямоугольниками(Х_нач, Х_кон, Число_шагов)
Сумма = 0;
h = (Х_кон-Х_нач)/Число_шагов;
х = Х_нач;
Для й=1 По Число_шагов Цикл
Сумма = Сумма + Функция_1(х + 0.5*h);
х = (х + h);
КонецЦикла;
Возврат h*Сумма;
КонецФункции
4) Метод трапеций:
Функция РассчитатьТрапециями(Х_нач, Х_кон, Число_шагов)
Сумма = 0;
h = (Х_кон-Х_нач)/Число_шагов;
х = Х_нач;
Для й=0 По Число_шагов Цикл
Если й=0 или й=Число_шагов Тогда
Сумма = Сумма + 0.5*Функция_1(х);
Иначе
Сумма = Сумма + Функция_1(х);
КонецЕсли;
х = х + h;
КонецЦикла;
Возврат h*Сумма;
КонецФункции
5) Метод Симпсона:
Функция РассчитатьСимпсона(Х_нач, Х_кон, Число_шагов)
Сумма = 0;
h = (Х_кон-Х_нач)/Число_шагов;
х = Х_нач;
СуммаЧетных = 0;
СуммаНеЧетных = 0;
Для й=0 По Число_шагов Цикл
Если й=0 или й=Число_шагов Тогда
Сумма = Сумма + Функция_1(х);
Иначе
Если й % 2 = 0 Тогда
СуммаЧетных = СуммаЧетных + Функция_1(х);
Иначе
СуммаНеЧетных = СуммаНеЧетных + Функция_1(х);
КонецЕсли;
КонецЕсли;
х = х + h;
КонецЦикла;
Возврат (h/3)*(Сумма + 2*СуммаЧетных + 4*СуммаНеЧетных);
КонецФункции
Итак, для рассматриваемого примера получились вот такие результаты:
Метод левых прямоугольников = 41,04375
Метод правых прямоугольников = 42,29375
Метод средних прямоугольников = 41,665625
Метод трапеций = 41,66875
Метод Симпсона = 41,6666666666666667
Точное же значение интеграла = 125/3 ~ 41,6(6). Чтож, неплохо.
В завершении нужно отметить, что вообще различных методов интегрирования существует довольно много, тем не менее, на практике большинство задач можно с успехом решать и этими.