Однажды мне попалась вот такая задача:
Пусть x и y два целых числа 1<x<y притом x + y≤100. Салли сказали только сумму x + y, а вот Полю произведение xy. Салли и Пол честнейшие ребята, это всем известно, они и друг другу отродясь не врали.
И вот такой вышел у них разговор:
Пол: «Не знаю я, что это за числа.»
Салли: «Тоже новость. Я знаю, что ты не знаешь.»
Пол: «Ну твоя то сумма мне теперь известна.»
Салли: «Да уж и мне теперь твое произведение.»
Каковы числа?
Идея решения пришла быстро, но отыскать его с помощью бумаги и карандаша оказалось трудно, поэтому пришлось обратиться к 1С.
Сначала определим алгоритм поиска. Хочу поблагодарить Сергея (ildarovich) за сделанное замечание, это позволило исправить первоначальный вариант, который давал правильные решения, но содержал ошибку
На предварительном этапе с помощью функции GetSallySum получим числа из заданного диапазона, которые нельзя представить в виде :
- суммы двух простых чисел;
- суммы простого числа и его квадрата;
- суммы простого числа и его куба.
При выполнении данной операции используется вспомогательная функция EratosthenesSieve для генерации списка простых чисел с помощью алгоритма "решето Эратосфена" Вот исходный код:
function EratosthenesSieve(Ulimit)
vt=new array(Ulimit+1);
for i=2 to Ulimit do
if vt[i]=undefined then
vt[i]=true;
j=i+i;
while j<=Ulimit do
vt[j]=false;
arr=new array;
for i=2 to Ulimit do
if vt[i]=true then
arr.Add(i);
endif;
enddo;
return arr;
endfunction
function GetSallySum(ULimit)
notsally=new array;
//в массив parr записываем все простые числа непревосходящие установленную границу
parr=EratosthenesSieve(Ulimit);
vt=new valuetable;
vt.Columns.Add("i",new ОписаниеТипов("Число"));
imax=parr.UBound();
for i=0 to imax do
for j=i to imax do
s=parr[i]+parr[j];
if s<ULimit then
row=vt.add();
row.i=s;
endif;
enddo;
s=parr[i]+parr[i]*parr[i];
if s<ULimit then
row=vt.add();
row.i=s;
endif;
s=parr[i]+parr[i]*parr[i]*parr[i];
if s<ULimit then
row=vt.add();
row.i=s;
endif;
enddo;
vt.GroupBy("i");
notsally=vt.ВыгрузитьКолонку("i");
sally=new array;
for s=4 to ULimit do
if notsally.Find(s)=undefined then
sally.Add(s);
endif;
enddo;
return sally;
endfunction
На следующем шаге мы готовим таблицу с числами кандидатами, среди которых будет искаться решение. Сумма этих чисел равна числу из массива, который возвращает предыдущая функция. Вот фрагмент кода:
vt=new valuetable;
vt.columns.Add("i",new ОписаниеТипов("Число"));
vt.columns.Add("j",new ОписаниеТипов("Число"));
vt.columns.Add("Multij",new ОписаниеТипов("Число"));
vt.columns.Add("Sumij",new ОписаниеТипов("Число"));
arr=GetSallySum(UpLimit);
for each sally in arr do
for i=2 to (sally-sally%2)/2 do
row=vt.Add();
row.i=i;
row.j=sally-i;
row.Sumij=sally;
row.Multij=row.i*row.j;
enddo;
enddo;
Теперь разберем структуру запроса. Временная таблица Candidate содержит исходные пары чисел, с рассчитанными для них значениями суммы и произведения. В таблице GroupMult мы собираем неповторяющиеся значения произведений. Затем из исходных данных отбираем только те строки, которые содержат уникальное значение произведения. Среди найденных строк находим неповторяющиеся значения для суммы. А затем применяем найденные значения, как фильтр к предыдущей выборке.
Приведу код, который я использовал при поиске решения. Сначала текст вспомогательной функции, которая помещает таблицу значений во временную таблицу, чтобы появилась возможность обращаться к ней в запросе. Аргумент МТТ - это ссылка на объект типа МенеджерВременныхТаблиц.
Функция PutToTemporaryTable(vt,name,MTT)
ТекстЗапроса="ВЫБРАТЬ
| ВходнаяТаблица.*
|ПОМЕСТИТЬ ВременнаяТаблица
|ИЗ
| &мТЗ КАК ВходнаяТаблица
|;";
запрос=новый Запрос;
запрос.Параметры.Вставить("мТЗ",vt);
запрос.текст=СтрЗаменить(ТекстЗапроса,"ВременнаяТаблица",name);
запрос.TempTablesManager=MTT;
запрос.Выполнить();
КонецФункции
Теперь функция, в которой реализован приведенный выше алгоритм.
function NumberOfSages() export
TTM=new МенеджерВременныхТаблиц;
vt=new valuetable;
vt.columns.Add("i",new ОписаниеТипов("Число"));
vt.columns.Add("j",new ОписаниеТипов("Число"));
vt.columns.Add("Multij",new ОписаниеТипов("Число"));
vt.columns.Add("Sumij",new ОписаниеТипов("Число"));
arr=GetSallySum(UpLimit);
for each sally in arr do
for i=2 to (sally-sally%2)/2 do
row=vt.Add();
row.i=i;
row.j=sally-i;
row.Sumij=sally;
row.Multij=row.i*row.j;
enddo;
enddo;
PutToTemporaryTable(vt,"Candidate",TTM);
query=new query;
query.МенеджерВременныхТаблиц=TTM;
query.Текст="ВЫБРАТЬ
| Candidate.Multij КАК Multij
|ПОМЕСТИТЬ GroupMult
|ИЗ
| Candidate КАК Candidate
|
|СГРУППИРОВАТЬ ПО
| Candidate.Multij
|
|ИМЕЮЩИЕ
| КОЛИЧЕСТВО(*) = 1
|;
|
|////////////////////////////////////////////////////////////////////////////////
|ВЫБРАТЬ
| Candidate.i КАК i,
| Candidate.j КАК j,
| Candidate.Multij КАК Multij,
| Candidate.Sumij КАК Sumij
|ПОМЕСТИТЬ FilterMult
|ИЗ
| Candidate КАК Candidate
| ВНУТРЕННЕЕ СОЕДИНЕНИЕ GroupMult КАК GroupMult
| ПО Candidate.Multij = GroupMult.Multij
|;
|
|////////////////////////////////////////////////////////////////////////////////
|ВЫБРАТЬ
| FilterMult.Sumij КАК Sumij
|ПОМЕСТИТЬ GroupSum
|ИЗ
| FilterMult КАК FilterMult
|
|СГРУППИРОВАТЬ ПО
| FilterMult.Sumij
|
|ИМЕЮЩИЕ
| КОЛИЧЕСТВО(*) = 1
|;
|
|////////////////////////////////////////////////////////////////////////////////
|ВЫБРАТЬ
| FilterMult.i КАК i,
| FilterMult.j КАК j,
| FilterMult.Multij КАК Multij,
| FilterMult.Sumij КАК Sumij
|ИЗ
| FilterMult КАК FilterMult
| ВНУТРЕННЕЕ СОЕДИНЕНИЕ GroupSum КАК GroupSum
| ПО FilterMult.Sumij = GroupSum.Sumij
|
|УПОРЯДОЧИТЬ ПО
| Sumij,
| Multij";
query.Parameters.Insert("UpLimit",UpLimit);
vt=query.Execute().UnLoad();
return vt;
EndFunction
Ответ приводить не буду. Приведу результаты своих исследований. В условиях задачи сумма чисел меньше или равна 37. Первое решение появляется, когда верхний предел становится равен 65. Второе решение появляется при верхнем пределе 439.
Послесловие.
В начале статьи я благодарю Сергея (ildarovich) за сделанное замечание. Он указал, что два различных числа больше единицы однозначно определяются по их произведению не только в случае, когда эти числа простые, но и в двух других, когда их произведение является либо кубом либо четвертой степенью простого числа. Во всех найденных мной в Сети решениях задачи о мудрецах говорится только о произведении простых чисел. Впрочем, с таким заявлением я поспешил, в этой статье такие варианты рассматриваются. Проведем поиск решения на конкретном примере . И так у нас есть таблица, которая содержит суммы двух чисел и их произведение. Значения произведений мы можем разбить на две группы, в первую отнесем повторяющиеся значения, во вторую неповторяющиеся.
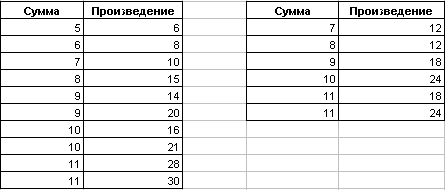
На приведенном рисунке в левой таблице содержатся неповторяющиеся произведения, в правой повторяющиеся. Данные построены для случая, когда сумма сомножителей меньше или равна 11. Внимательный читатель сразу заметит, что к неповторяющимся отнесено произведение 20, хотя 20 равно 4*5 и 2*10. Точно так же не подходят под критерий неповторяющихся произведения 28 и 30. Все дело в ограничении на сумму. Для числа 20 сумма множителей 4 и 5 равна 9 и эта пара попадает в исследуемый набор, а сумма множителей 2 и 10 равна 12, что больше верхнего предела. Поэтому эта пара в наборе отсутствует. Отсюда первый вывод , то куда попадет произведение из исходной последовательности зависит от ограничения на сумму сомножителей.
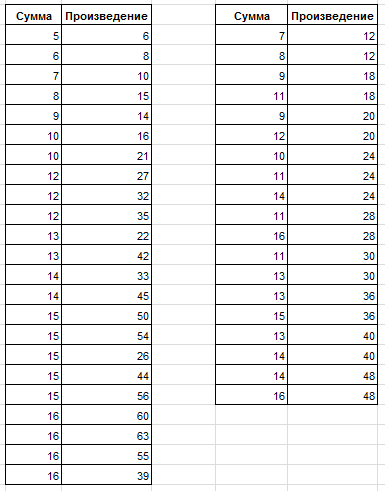
Если мы будем рассматривать набор чисел, для которых сумма множителей меньше 16, то увидим что значения 20,28 и 30 исчезли из левой таблицы. Это подтверждают данные на приведенном рисунке. Следующий шаг заключается в поиске таких значений из колонки Сумма, которые не встречаются в левой таблице, но присутствуют в правой. В последнем примере таким числом является 11. И обнаружить мы это можем только начиная с суммы множителей равной 16. Вот и второе наблюдение, список чисел, которые не выражаются в виде суммы сомножителей, чье произведение не повторяется в рассматриваемом наборе, зависит от размера этого набора. Ниже приведен список таких чисел. В колонке Предел проставлено значения верхнего предела суммы множителей, при котором появляется данное значение. Такие суммы назовем числами Салли.
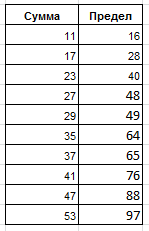
Решения нашей задачи нам нужно искать среди таких пар, у которых значение суммы содержится в приведенном выше наборе. Найденные пары опять разобьем на две группу. В первую занесем те значения, которые не содержат повторяющиеся значения из колонки Произведение, во вторую отнесем пары с повторяющимися значениями произведения. Ниже приводятся таблицы для случая, когда сумма множителей меньше 64.
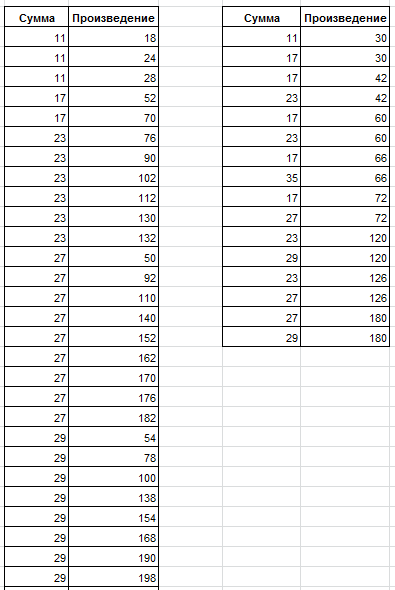
Левая таблица показана не полностью. Обратим внимание на две пары из левой таблицы - (17;52) и (17;70). Увеличим верхнюю границу до 65. Согласно нашим данным при этом ограничении появляется число Салли равное 37.
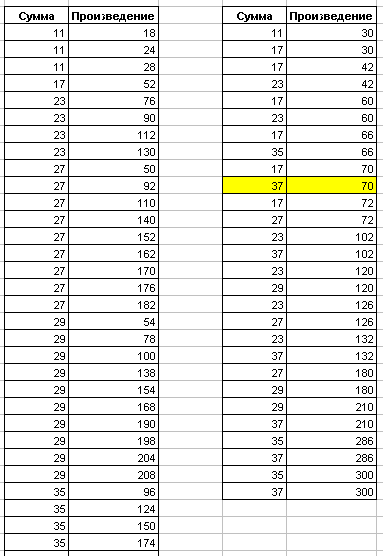
37 можно представить в виде суммы двух чисел 2 и 35. Их произведение равно 70. Значит произведение со значением 70 стало повторяющимся, появилось две пары (17;70) и (37;70). Поэтому пара (17;70) из левой таблицы уйдет. И в левой таблице появится пара (17;52) , у которой значение из колонки Сумма уникальное. И эта пара будет первым решением задачи о числах мудрецов.
В изложенном подходе мы обрабатывали исключительно набор данных образованных парами, составленными из значений суммы и произведения двух множителей. В этом случае состав множества чисел, которые мы назвали числа Салли, определяется верхней границей для суммы сомножителей. В тоже время, существует альтернативный подход для построения чисел Салли. На первом шаге мы можем сгенерировать ряд простых чисел. На следующем составить множество из попарной суммы простых чисел и сумм вида (p+p*p), а также (p+p*p*p), где p - это простое число. А затем найти числа, которые не вошли в указанный набор, но больше его нижней границы и меньше верхней. Именно такой подход я использовал. Результаты, которые дает запрос Сергея (ildarovich) и подход с использованием генерации чисел Салли совпадают. Отличие заключается в значении суммы множителей, при которых эти решения появляются. Ниже приводится ряд образованный значениями ограничений на сумму, при которых появляются новые решения задачи, если использовать генератор чисел Салли - 37,439,757,991,1267,1925,2023,2227,2323. Запрос Сергея дает первое решение при верхней границе - 65 (это показано в разобранном примере) , второе при верхней границе 1685.
Ну и наконец, заключительная таблица с числами мудрецов.
| число А | число В | Сумма | Произведение |
| 4 | 13 | 17 | 52 |
| 4 | 61 | 65 | 244 |
| 16 | 73 | 89 | 168 |
| 16 | 111 | 127 | 1 776 |
| 64 | 73 | 137 | 4 672 |
| 32 | 131 | 163 | 4 192 |
| 4 | 229 | 233 | 916 |
| 32 | 311 | 343 | 9 952 |
| 64 | 309 | 373 | 19 776 |