Введение
Когда-то прочитав публикацию на Зазеркалье о добавлении в платформу метода решения систем линейных уравнений (СЛАУ), был заинтересован, так как раньше немного интересовался алгоритмами решения СЛАУ. Особенно заинтриговала публикаций от 1С на хабре, где они показывают очень уж сильные результаты по времени в сравнении с известными библиотеками. Недавно найдя свои старые наработки по Matlab в части моделирования электромагнитного поля, где как раз и возникают большие линейные уравнения с разреженной, несимметричной матрицей коэффициентов, которые плохо поддаются решению, решил проверить, что покажет на них 1С.
Что сравниваем?
Сравниваем следующие методы:
- Реализация в 1С, про который немного известно, но судя по описанию с ИТС, у них используется как прямой метод решения, так и итерационный метод, а так же ряд своих оптимизаций, ключевая из которых - это разбить систему на много мелкий, что значительно облегчает поиск решения. Тот или иной метод выбирается в зависимости от вида СЛАУ (разряженные, симметричная и т.д.) и настроек, переданных разработчиком. Так же упоминается, что используются возможности многоядерных процессоров.
- Реализация в Matlab, которая работает по умолчанию при расчете уравнений x=A\b, где А - коэффициенты уравнений СЛАУ, b-свободные коэффициенты. Matlab так же в зависимости от вида СЛАУ выбирает тот или иной метод. В нашем случае для несимметричных, разреженных матриц (А) будет использоваться метод UMFPACK (V5.4.0 (May 20, 2009), BLAS library used: Fortran BLAS). В свое время выбирая разные методы для своей задачи остановился на нем из-за его всеядности и скорости решения. Метод относится к прямым методам - за конечное число шагов позволяет получить результат. Судя по информации из интернета эта реализация не поддерживает возможности многоядерных процессоров.
Тест №1
Возьмем простой пример для понимания процесса оформления решения СЛАУ в системе 1С (на ИТС есть описание):
(1) 1*X1 + 1*X2 + 1*X3 = 2
(2) 5*X1 + 0*X2 + 6*X3 = 3
(3) 4*X1 + 4*X2 + 0*X3 = 4
Для решения нам надо сделать 5 шагов:
- Описать таблицу коэффициентов уравнения (то, что слева в системе уравнений от знака равенства)
- Описать таблицу свободных коэффициентов уравнения (то, что справа в системе уравнений от знака равенства)
- Создать объект платформы РасчетСистемЛинейныхУравнений
- Указать таблицы-источники данных уравнения и связываем колонки полей с настройками объекта РасчетСистемЛинейныхУравнений
- Расчет
Получим "решение" (из трех неизвестных переменных в ответе только одна):
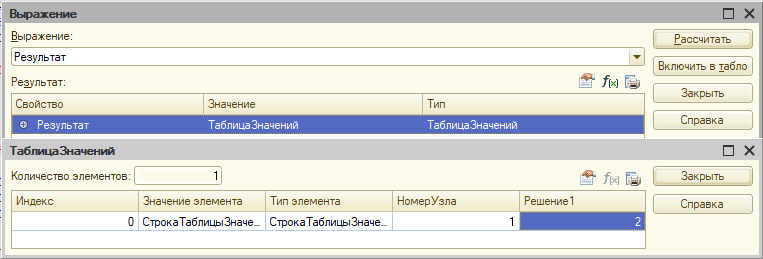
Некорректное решение
Однако, если мы не будет добавлять в таблицу нулевые коэффициенты, то есть напишем условие, исключающее их:
Коэффициент = Число(СокрЛП(КоэффициентыУравнения[НомерПеременной]));
Если Коэффициент <> 0 Тогда
Строка = МатрицаКоэффициентов.Добавить();
Строка.НомерУравнения = НомерУравнения + 1;
Строка.НомерПеременной = НомерПеременной + 1;
Строка.Коэффициент = Коэффициент;
КонецЕсли;
получим корректное решение:
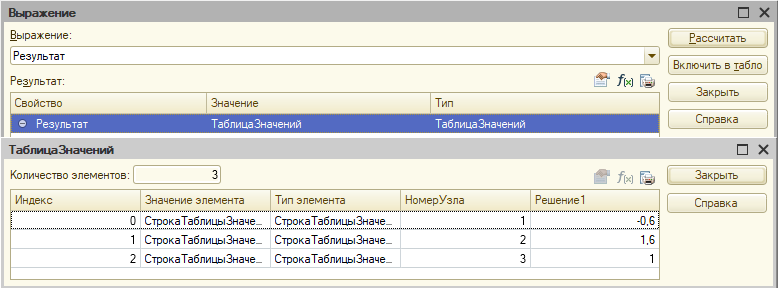
Корректное решение
Проблема №1: нулевые коэффициенты задавать не нужно, поведение неописанное, значит подходит на ошибку платформы. Косвенно верно, что нет необходимости вставлять нулевые коэффициенты, 1с заявляет решение больших разряженных систем, где нулевые коэффициенты наиболее встречаемые, и если их задавать, скажем в матрице 200 000 х 200 000, может памяти и не хватить, учитывая, что язык 1с интерпретируемый.
Проблема №2: из коробки нельзя проверить решение, только реализовав функцию умножения матриц и вычисления нормы (в нашем случае тоже, что и длина вектора), это не сложно, но зачем, если есть объект решения в платформе и мог бы возвращать точность решения или признак, достигнута ли требуемая точность.
Тест №2
Как известно, решение СЛАУ используется в типовых конфигурациях уровня предприятия для нахождения себестоимости, например, продукции. Рассмотрим 1С:Комплексную конфигурацию 2.5 (2.5.9.135) и процедуру расчета себестоимости, посмотрим, как там отрабатывает механизм решения СЛАУ. У меня под рукой небольшая по номенклатуре база с производством продукции. При закрытии месяца отрабатываются различные расчеты СЛАУ, мы будем рассматривать функцию РасчетСебестоимостиРешениеСЛУ.РешитьСЛУПлатформой_СебестоимостьОрганизаций, точнее часть, представленную ниже, где мы возьмем одну СЛАУ, а ее данные и решение сохраним в файл, чтобы проанализировать отдельно, расчет отрабатывает без ошибок и закрытие месяца проходит удачно:
Чтобы визуально посмотреть, с какой матрицей имеем дело, таблицу коэффициентов визуализировал в Matlab, результат ниже, матрица квадратная, разреженная и несимметричная.
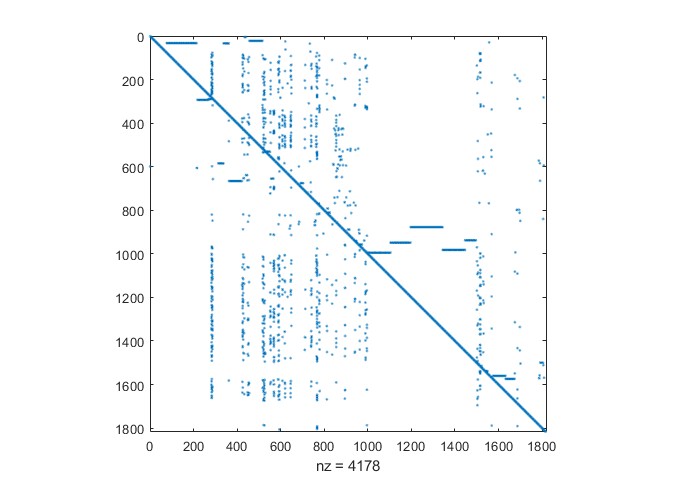
Вид матрицы коэффициентов, полученной при расчете себестоимости
Так же интересен вопрос, есть ли нулевые коэффициенты в данных. Таких элементов не оказалось, поэтому есть шанс, что не попадем на Проблему №1. Выгрузив/загрузив данные в Matlab для проверки решения, оказалось, что если решение 1С подставить в исходную СЛАУ и вычесть свободные коэффициенты, то получим норму (norm (A*x-b)): 1.7095 * 107 . Норма должна стремится к 0 и чем ближе, тем точнее решение. Рассчитанная норма говорит о том, что получено точно не решение уравнения. Перебирая параметры РасчетСистемЛинейныхУравнений (точность, количество итераций и т.д.), я так и не смог получить что-то адекватное, а отсутствие ошибок встроенного языка говорит косвенно о том, что мы делаем все верно. Визуально сравнивая попеременно решения 1С и Matlab, как показано ниже, есть много совпадений по результатам, возможно, оптимизатор 1с разбивает решение на множество мелких СЛАУ, часть которых сходится к решению, а часть нет.
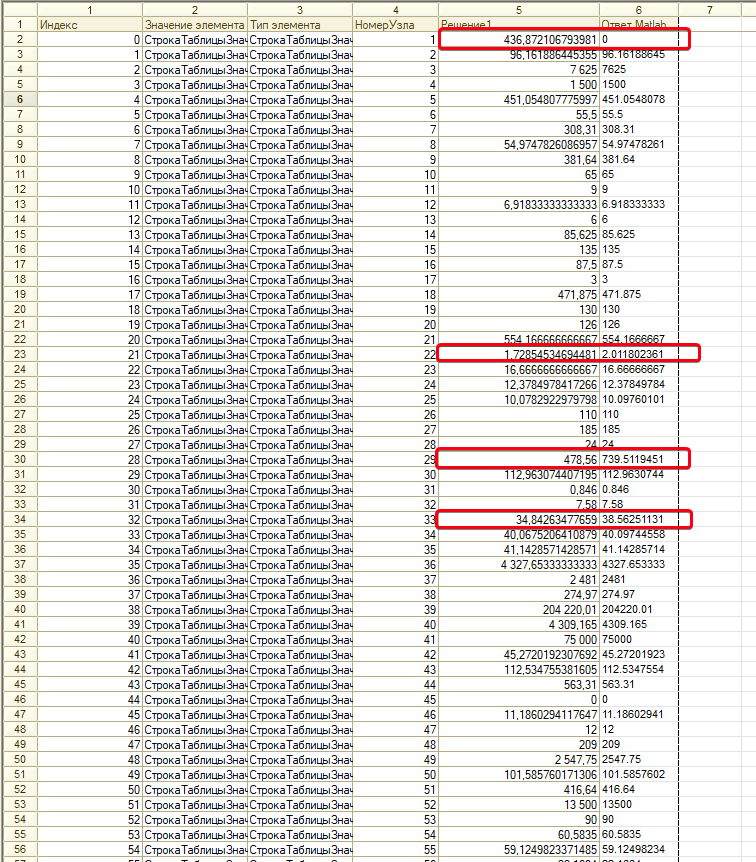
Сравнение решений 1С и Matlab
Проведя закрытие за разные месяца, так и не удалось получить решение с заданной точностью.
Результат
Мы так и не добрались до сравнения графиков скорости работы, потому как на текущий момент сравнивать нечего, 1С отказывается решать СЛАУ с заданной точностью. О найденных ошибках сообщил в 1С, они порекомендовали обновить Комплексную конфигурацию, но надеюсь пробить первую линию и добраться до разработчиков. Если я не ошибаюсь в выводах и все вычисления провел корректно, то потенциально во многих базах на себестоимость стоит обратить внимание. К Тесту №3 - сравнение скорости решений, можно будет вернуться, когда разрешится вопрос с полученными результатами. Тестирование проводилось на платформе 1С версии 8.3.22.1709.
Update 28.11.2022: Вопрос передали в отдел разработки, номер - 60004240