Алгоритм, рассмотренный в статье, называется методом Сугиямы. Ограничения: можно строить только связные ориентированные ациклические графы. В некоторых случаях некоторые шаги можно пропускать, например, разбиение на уровни (п.2) может задаваться вместе с графом, если изображаются события, связанные временной зависимостью. В этом случае выполняются только последние два шага.
Посмотрим как дела обстоят в конфигурациях 1С, без использования типовых бизнес-процессов.
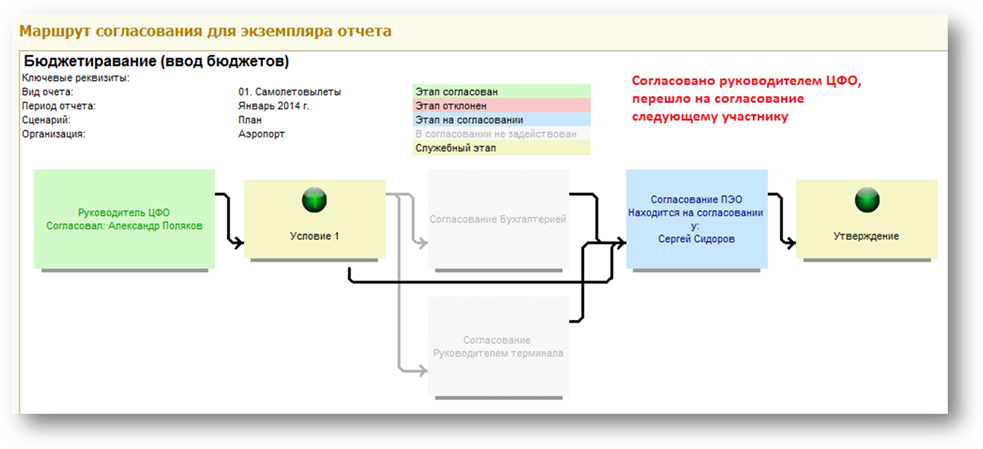
Как графы строят в конфигурации Управление Холдингом:
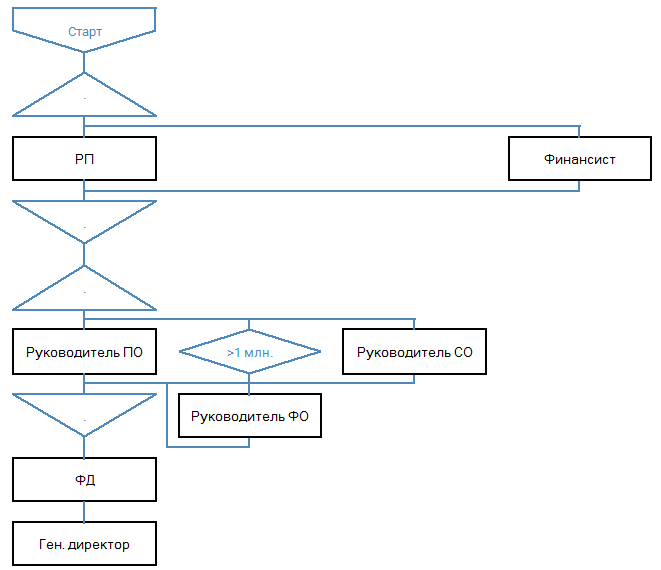
Как графы строят в БИТ.Финанс:
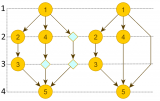
Как видите, самые частые ошибки:
1. Некорректное расположение вершин по вертикали: вершина-источник и вершина-приемник могут находится на одном уровне;
2. Пересечение ребер, там где их можно избежать;
3. Некорректное расположение вершин по горизонтали. В примере БИТа вершина финансист должна быть сильно левее.
Как получается строить графы у нас:
Тренироваться будем на примере процессов БИТ.Финанс. Сразу хочу предупредить, что готового кода здесь нет.
Часть первая: теория.
0. Исходный граф
Для примера я взял вот такой граф. В конце статьи вы увидите, каким он в результате получился.
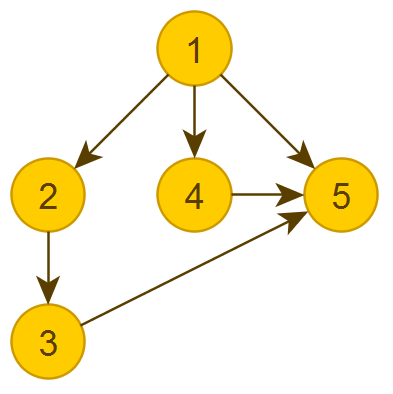
1. Проверка на ацикличность. Построение матрицы смежности.
1.1. Алгоритм проверки на ацикличность.
В первую очередь нам необходимо проверить, является ли то, что мы хотим изобразить - связным ориентированным ациклическим графом. Для этого обойдем все вершины графа (поиск в глубину), но с особенностями: каждую посещенную вершину мы будем окрашивать в цвет.
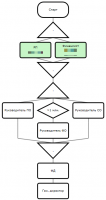
Изначально все вершины графа имеют статус "Не посещалась" (белый цвет). Начинаем последовательно идти по вершинам графа и помечаем их статусом "В обработке" (серый цвет). Если у вершины нет необработанных дочерних вершин, то отмечаем ее как "Обработана" (черный цвет). Если в процессе обхода одной ветки попадаем на статус "В обработки" (серый цвет), значит есть цикл. Далее обходим непосещенные вершины пока они не закончатся. ВАЖНО! В черные вершины второй раз не заходим!
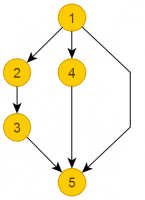
Пример: ациклический граф (корректный граф).
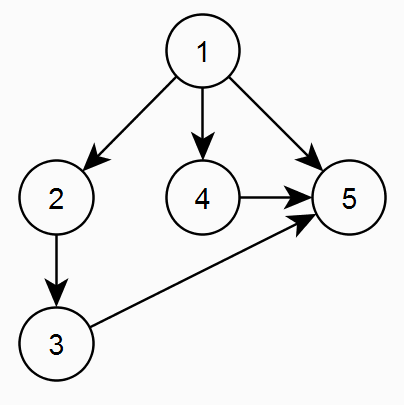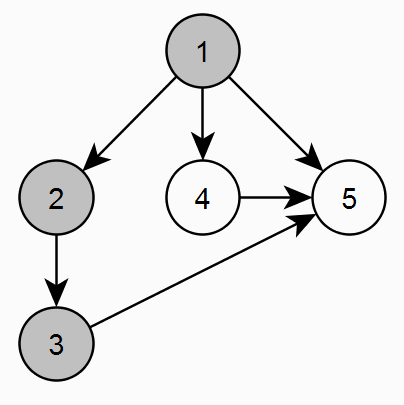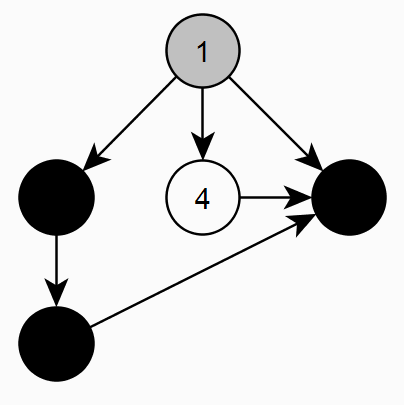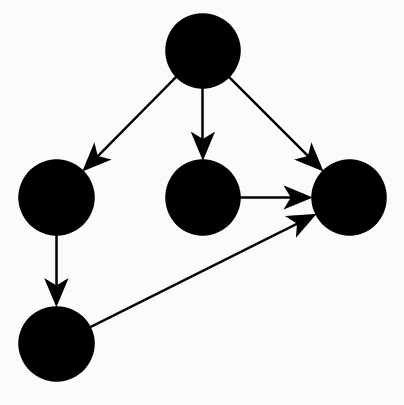
Пример: циклический граф (некорректный граф).
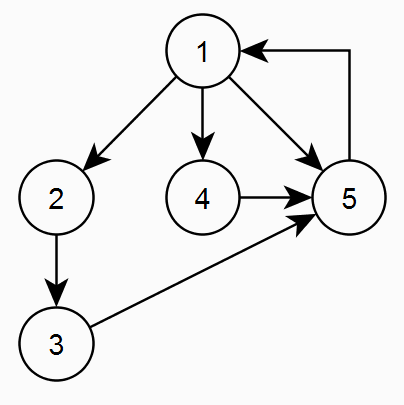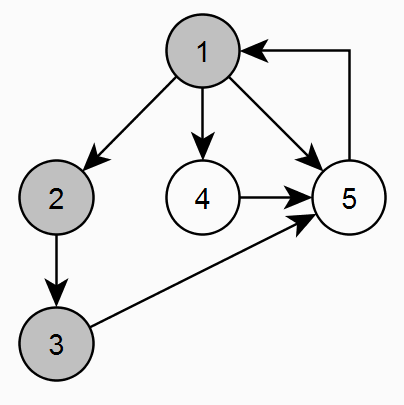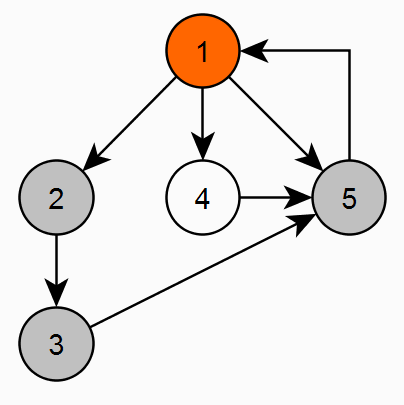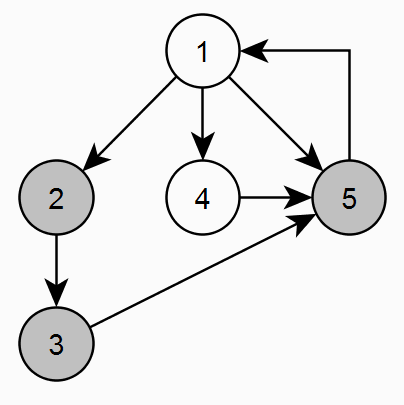
На этом этапе мы определили является ли граф ациклическим.
1.2. Матрица смежности
Пока обходим граф для проверки ацикличности, заодно строим матрицу смежности. Матрица смежности - это матричное представление графа, где единицей указывается связь между вершинами:
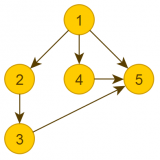
Наш граф:

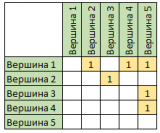
Матрица для него будет такой:

В строках указаны вершины-источники, в колонках вершины-приемники. Видно что вершина 1 и вершина 2 связаны ребром и т.д.
На данном этапе мы получили матричное представление графа.
2. Поуровневое расположение вершин графа.
Поуровневое расположение вершин необходимо для исключения ошибок расположения вершин по вертикали, например, чтобы вершина-приемник не была выше вершины-источника.
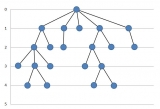
Пример расположения:
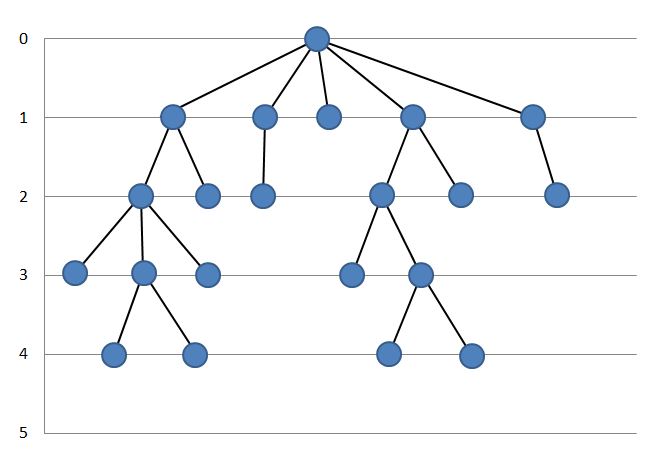
Граф надо расположить по уровням таким образом, чтобы:
1. Вершины-источники были выше чем вершины-приемники.
2. Ребро должно быть не длиннее одного уровня. Достигается это с помощью добавления фиктивных вершин.
3. Опционально: могут быть условия на предельную ширину/высоту и т.д. В данном материале дополнительные условия не рассматриваем. Ниже будут ссылки с более подробной информацией.
Если изобразить визуально.
Исходный граф:

Граф, разбитый по уровням. Слева с фиктивными вершинами, справа - результат:
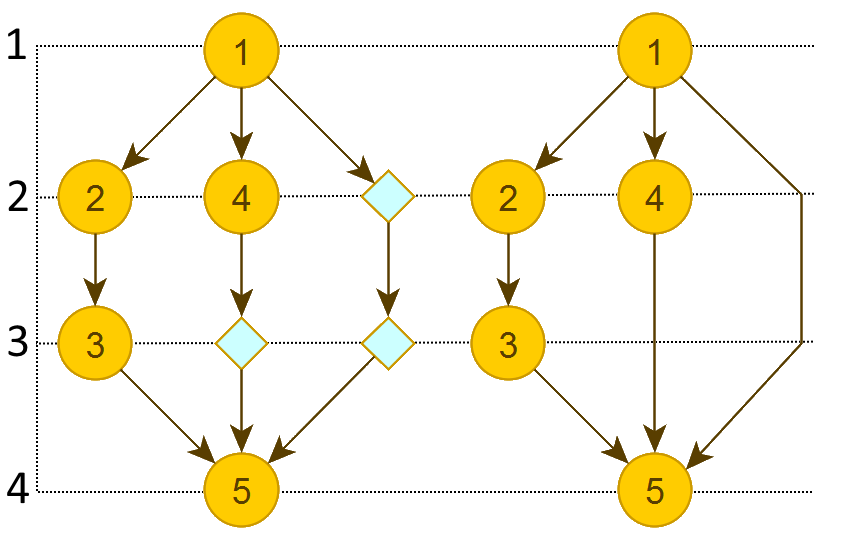
Алгоритм состоит из двух частей: проход от стоков (вершин без исходящих ребер) и проход от вершин-источников. Зачем проходить два раза? Потому что ширина при разных проходах может различаться. Оптимальнее выбирать наименьшую ширину.
Начнем с прохода от стоков.
2.1. Берем вершины, которые не имеют исходящих ребер (конечные точки). Располагаем на исходном уровне.
2.2. Берем вершины, которые входят в эту вершину с одним ребром (без альтернативных путей).
2.3. Повторяем п.2 n-раз пока не обойдем все вершины.
2.4. Достраиваем ребра длиннее одного уровня, через фиктивные вершины.
Исходный граф:

Гифка прохода от стоков:

Проход в обратную сторону по тому же алгоритму, только начинается от вершин-источников.

Дальше выбирается минимальная ширина графа: минимальное количество вершин на одном уровне. В нашем случае ширина одинаковая, поэтому берем любой из вариантов.
Я взял вариант с пересечениями, чтобы продемонстрировать следующий шаг.
3. Минимизация количества пересечения ребер.
После расположения графа по уровням, может случится так что некоторые ребра имеют пересечения. Цель третьего шага: минимизация пересечений.
Алгоритм очень простой:
3.1. Обходим граф (поиск в глубину) и нумеруем вершины, в том числе фиктивные.
3.2. Упорядочиваем на каждом уровне вершины по возрастанию.
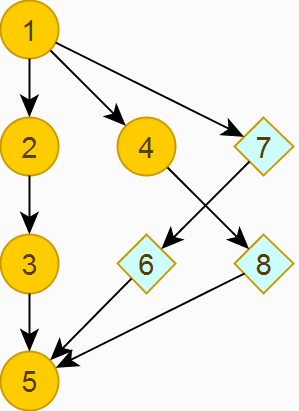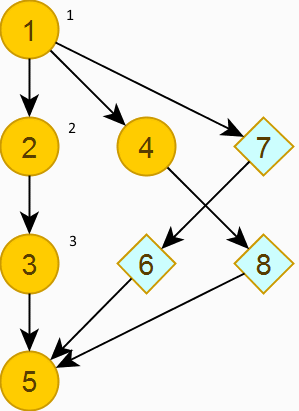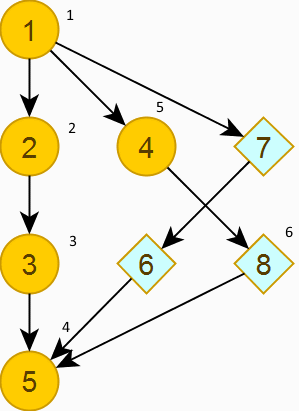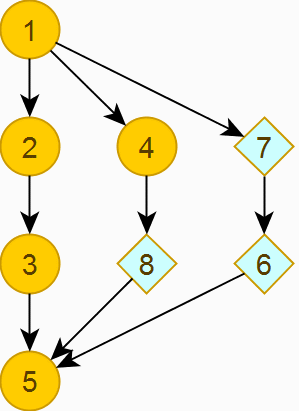
Переходим к заключительному шагу.
4. Размещение вершин графа внутри одного уровня (по оси x-координат).
Нам нужно красиво расположить наши вершины на каждом уровне. Один из самых простых вариантов - выравнивание по центру. Но есть более сложные варианты.
Мой результат для исходного графа
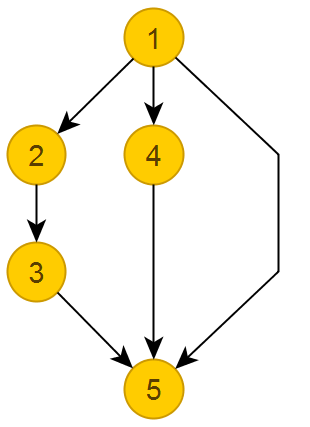
Подробная информация по вариантам размещения по x-координатам изложена здесь. Там же можно почитать более подробно о поуровневом расположении графов, например, как построить циклический граф таким способом, как минимизировать высоту или ширину графа и много-много другого.
И самое крутое - апплет на java. Можно поиграться с различными вариантами расположения. Ссылка на апплет.
5. Визуализация HTML + SVG.
Визуализировать можно с помощью табличного документа - рисовать линии по координатам. Это самый простой и понятный вариант. Так делает БИТ, да и в Консолидации также, скорее всего.
Но мы пошли другим путем. Взяли координаты наших вершин и нарисовали их с помощью HTML + SVG. С помощью SVG можно унылый табличный документ превратить в красоту. Здесь обучалка по основным возможностям SVG. Мне очень понравилось работать с этим форматом, попробуйте и вы:)
Часть вторая: практика.
А практику можно пройти у нас в компании. Мы покажем, как это реализовано у нас, и научим подобным крутым штукам.
У нас открыты вакансии программистов и аналитиков как на проектную работу, так и в штат. Welcome! Ну или пишите в личку.

Вступайте в нашу телеграмм-группу Инфостарт