Основы компьютерной графики (часть 2)
Выводы из первой части
Во второй части мы будем использовать весь накопленный опыт первой части. Перечислим итоги первой части статьи:
- Выполнять операции преобразования можно с помощью умножения специально заполненных матриц 3х3.
- С помощью матриц 3х3 можно накапливать результаты операций преобразований.
- Используя несколько матриц, можно организовать вставку преобразования в любое место цепочки преобразований.
Переходим к 3D
На этом моменте многих ждет разочарование. Расчет координат в 3-м мерном пространстве не сильно отличается, от расчета координат в 2-мерном пространстве.
Матрица точки теперь выглядит так (x,y,z,1)
Матрица перемещения
Матрица масштабирования
где X,Y,Z – коэффициенты масштабирования по соответствующим координатам
С вращением немного сложнее, ключевое слово «немного». Для начала определим как расположены оси координат. Центр координат расположен в центре экрана (отображаемой области). Ось X – направлена вправо, ось Y – направлена вверх, ось Z – направлена перпендикулярно плоскости монитора в даль, в геометрии обычно обозначают «х» - хвост стрелы.
Надеюсь, многие поняли, что в первой части вы выполняли вращение в плоскости Y0X вокруг оси Z, т.е. у нас уже есть готовая матрица поворота вокруг оси Z.
Матрицы поворота вокруг осей X,Y выводятся подобным образом.
Матрица поворота вокруг оси X
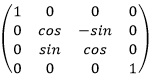
Матрица поворота вокруг оси Y
Программный код для вычисления координат в 3-мерном пространстве не многим отличается от кода для 2-мерного пространства.
Ортографическая проекция
Координаты вычислили, но монитор плоский, маловероятно, но возможно, у кого-то и не плоский, но экран все равно плоский. Как выводить 3-х мерное изображение на плоский экран?
Мы будем проецировать изображение на (плоскость Y0X). Для начала мы построим ортографическую проекцию – координаты x, y не будут изменятся в зависимости от координаты z. Такие проекции строят, как правило, САПР (системы автоматизированного проектирования), где важно сохранение пропорций и размеров, а не реалистичность.
Теперь у нас уже не квадрат а куб. Точек стало больше, отрезки превратились в ребра, и стало их соответственно тоже больше.
&НаКлиенте
Процедура Инициализация()
Куб = Новый Структура("Матрицы,Ребра,Точки,Владелец");
Куб.Владелец = Неопределено;
Точки = Новый Массив();
Точки.Добавить(ПолучитьТочку(-10, -10, -10));
Точки.Добавить(ПолучитьТочку(-10, 10, -10));
Точки.Добавить(ПолучитьТочку(10, 10, -10));
Точки.Добавить(ПолучитьТочку(10, -10, -10));
Точки.Добавить(ПолучитьТочку(-10, -10, 10));
Точки.Добавить(ПолучитьТочку(-10, 10, 10));
Точки.Добавить(ПолучитьТочку(10, 10, 10));
Точки.Добавить(ПолучитьТочку(10, -10, 10));
Куб.Точки = Точки;
Ребра = Новый Массив();
Ребра.Добавить(ПолучитьРебро(0,1));
Ребра.Добавить(ПолучитьРебро(1,2));
Ребра.Добавить(ПолучитьРебро(2,3));
Ребра.Добавить(ПолучитьРебро(3,0));
Ребра.Добавить(ПолучитьРебро(4,5));
Ребра.Добавить(ПолучитьРебро(5,6));
Ребра.Добавить(ПолучитьРебро(6,7));
Ребра.Добавить(ПолучитьРебро(7,4));
Ребра.Добавить(ПолучитьРебро(0,4));
Ребра.Добавить(ПолучитьРебро(1,5));
Ребра.Добавить(ПолучитьРебро(2,6));
Ребра.Добавить(ПолучитьРебро(3,7));
Куб.Ребра = Ребра;
М = ПолучитьЕдиничнуюМатрицу4х4();
М[0][0] = 3;
М[1][1] = 3;
М[2][2] = 3;
М[3][2] = 20;
Куб.Матрицы = Новый Массив();
Куб.Матрицы.Добавить(М);
ВывестиОбъект(Куб);
КонецПроцедуры
Все преобразования выполняются схожим образом.
&НаКлиенте
Функция ПолучитьМатрицуПоворотаZ(Угол)
М = ПолучитьЕдиничнуюМатрицу4х4();
Pi = 3.1415926535897932;
УголРадианы = Угол / 180 * Pi;
Косинус = Cos(УголРадианы);
Синус = Sin(УголРадианы);
М[0][0] = Косинус;
М[0][1] = -Синус;
М[1][0] = Синус;
М[1][1] = Косинус;
Возврат М;
КонецФункции
&НаКлиенте
Процедура КомандаПоворотZ(Команда)
// Вставить содержимое обработчика.
М = ПолучитьМатрицуПоворотаZ(УголПоворота);
Если МестоВставки = 0 Тогда
УмножитьМатрицы4х4(М, Куб.Матрицы[0]);
Куб.Матрицы[0] = М;
Иначе
УмножитьМатрицы4х4(Куб.Матрицы[0], М);
КонецЕсли;
ВывестиОбъект(Куб);
КонецПроцедуры
Получение координат после всех преобразований:
&НаКлиенте
Функция ПолучитьМатрицуПреобразований(Объект)
М = ПолучитьЕдиничнуюМатрицу4х4();
Для Каждого Матрица Из Объект.Матрицы Цикл
УмножитьМатрицы4х4(М, Матрица);
КонецЦикла;
Если Объект.Владелец <> Неопределено Тогда
Для Каждого Матрица Из Объект.Владелец.Матрицы Цикл
УмножитьМатрицы4х4(М, Матрица);
КонецЦикла;
КонецЕсли;
Возврат М;
КонецФункции
&НаКлиенте
Функция ПолучитьКоордиантыТочек(Объект, МатрицаПреобразований)
рТочки = Новый Массив();
Для Каждого Точка Из Объект.Точки Цикл
рТочка = Новый Массив(4);
рТочка[0] = Точка[0] * МатрицаПреобразований[0][0] + Точка[1] * МатрицаПреобразований[1][0] + Точка[2] * МатрицаПреобразований[2][0] + Точка[3] * МатрицаПреобразований[3][0];
рТочка[1] = Точка[0] * МатрицаПреобразований[0][1] + Точка[1] * МатрицаПреобразований[1][1] + Точка[2] * МатрицаПреобразований[2][1] + Точка[3] * МатрицаПреобразований[3][1];
рТочка[2] = Точка[0] * МатрицаПреобразований[0][2] + Точка[1] * МатрицаПреобразований[1][2] + Точка[2] * МатрицаПреобразований[2][2] + Точка[3] * МатрицаПреобразований[3][2];
рТочка[3] = Точка[0] * МатрицаПреобразований[0][2] + Точка[1] * МатрицаПреобразований[1][2] + Точка[2] * МатрицаПреобразований[2][2] + Точка[3] * МатрицаПреобразований[3][3];
рТочка[0] = рТочка[0] + 80;
рТочка[1] = -рТочка[1] + 80;
рТочки.Добавить(рТочка);
КонецЦикла;
Возврат рТочки;
КонецФункции
&НаКлиенте
Процедура ОбновитьКоординатыРебер(Объект, Точки)
Для Каждого Ребро Из Объект.Ребра Цикл
Линия = Ребро[0];
Точка1 = Точки[Ребро[1]];
Точка2 = Точки[Ребро[2]];
Линия.Лево = Точка1[0];
Линия.Верх = Точка1[1];
Линия.Ширина = Точка2[0] - Точка1[0];
Линия.Высота = Точка2[1] - Точка1[1];
КонецЦикла;
КонецПроцедуры
Результат выглядит так.
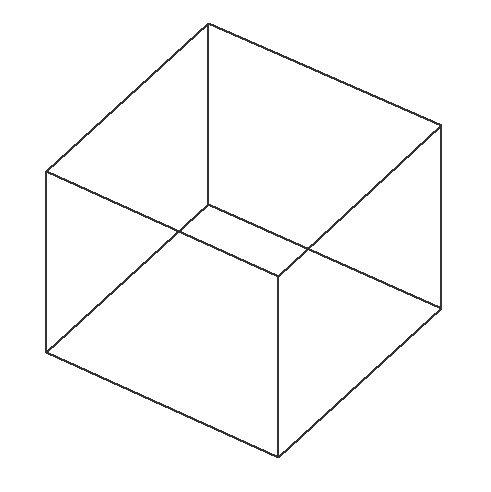
Выделение невидимых граней куба
На предыдущем скриншоте у нас получился каркас куба. У проекции куба не все грани должны отображаться. Как определить должна отображаться грань либо нет?
У грани есть две поверхности лицевая и задняя. Если грань повернута в экран лицевой поверхностью, значит её нужно отображать, иначе нет.
Для определения какой поверхностью грань повернута к экрану, воспользуемся следующим свойством:
Векторное произведение двух векторов в трехмерном евклидовом пространстве - вектор, перпендикулярный обоим исходным векторам. В нашем случае перпендикулярный грани. Координата Z как раз показывает в экран направлен вектор, либо наоборот.
Произведение векторов находится следующим образом:
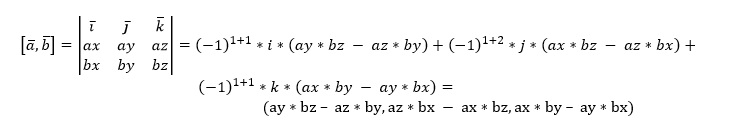
Нас интересует только составляющая вектора z, которая у нас получилась равна ax* by – ay* bx .
Теперь у нашего куба появились грани, которые состоят из точек и ребер. Для грани важен порядок точек, я указал по порядку, в направлении хода часовой стрелки.
&НаКлиенте
Процедура Инициализация()
Куб = Новый Структура("Матрицы,Ребра,Точки,Владелец,Грани");
Куб.Грани = Новый Массив();
Куб.Грани.Добавить(ПолучитьГрань(0,1,2,3,0,1,2,3));
Куб.Грани.Добавить(ПолучитьГрань(1,5,6,2,9,5,10,1));
Куб.Грани.Добавить(ПолучитьГрань(3,2,6,7,2,10,6,11));
Куб.Грани.Добавить(ПолучитьГрань(0,3,7,4,3,11,2,8));
Куб.Грани.Добавить(ПолучитьГрань(0,4,5,1,8,4,9,0));
Куб.Грани.Добавить(ПолучитьГрань(4,7,6,5,7,6,5,1));
КонецПроцедуры
&НаКлиенте
Функция ПолучитьГрань(Т0,Т1,Т2,Т3,Р0,Р1,Р2,Р3)
Грань = Новый Структура("Точки,Ребра");
Грань.Точки = Новый Массив(4);
Грань.Точки[0] = Т0;
Грань.Точки[1] = Т1;
Грань.Точки[2] = Т2;
Грань.Точки[3] = Т3;
Грань.Ребра = Новый Массив(4);
Грань.Ребра[0] = Р0;
Грань.Ребра[1] = Р1;
Грань.Ребра[2] = Р2;
Грань.Ребра[3] = Р3;
Возврат Грань;
КонецФункции
С наименованиями свойств я особо не заморачивался, и уже в таком небольшом коде, можно запутаться, иногда точки - это координаты точек, а иногда индексы точек, тоже самое и с ребрами.
Возможно кому-то кажется, что было бы изящнее вместо куба взять более интересный объект, например, сделать объемную запись 1С. Во-первых на кубе - объяснять проще, а во-вторых - я уже даже на кубе запутался сам с ребрами, где-то в грани указал неправильный индекс ребра.
Изначально я хотел невидимые ребра выводить пунктирной линией, а видимые сплошной, но реализовать это оказалось не просто, т.к. свойство «тип линии», оказалось, доступным только для чтения. Остановился на том что видимые ребра – синие, невидимые – зеленные.
Добавляем определение видимости граней в код.
&НаКлиенте
Процедура ВывестиОбъект(Объект)
МатрицаПреобразований = ПолучитьМатрицуПреобразований(Объект);
Точки = ПолучитьКоордиантыТочек(Объект, МатрицаПреобразований);
ОбновитьКоординатыРебер(Объект, Точки);
ОпределитьВидимостьГраней(Объект, Точки);
КонецПроцедуры
Реализация
&НаКлиенте
Процедура ОпределитьВидимостьГраней(Объект, Точки)
Для Каждого Ребро Из Объект.Ребра Цикл
Линия = Ребро[0];
Линия.ЦветЛинии = Новый Цвет(0,150,0);
КонецЦикла;
Для Каждого Грань Из Объект.Грани Цикл
Точка0 = Точки[Грань.Точки[0]];
Точка1 = Точки[Грань.Точки[1]];
Точка2 = Точки[Грань.Точки[2]];
Ах = Точка1[0] - Точка0[0];
Ау = Точка1[1] - Точка0[1];
Вх = Точка2[0] - Точка1[0];
Ву = Точка2[1] - Точка1[1];
Z = Ах * Ву - Ау * Вх;
//Сообщить(Z);
Если Z < 0 Тогда
Для Каждого ИндексРебра Из Грань.Ребра Цикл
Линия = Объект.Ребра[ИндексРебра][0];
Линия.ЦветЛинии = Новый Цвет(0,0,150);
КонецЦикла;
КонецЕсли;
КонецЦикла
КонецПроцедуры
Результат.
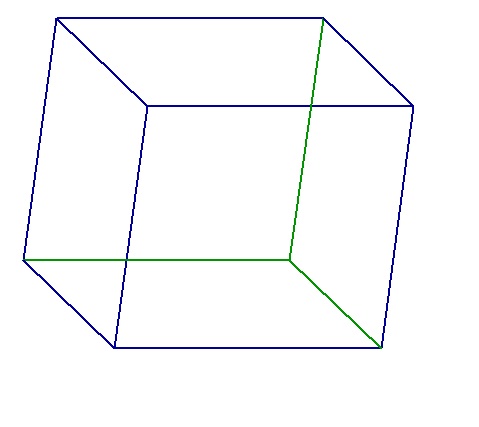
Не сразу понятно, что куб наклонен вниз.
Перспективная проекция
Добавим еще реалистичности нашему изображения. На зрачок человеческого глаза попадает, конечно, не ортографическая проекция, а перспективная. Добиться настоящей реалистичности очень сложно, тут очень много факторов: у человека два глаза, зрачок умеет фокусироваться, изменять чувствительность к яркости, кроме того полученное изображение обрабатывается мозгом. Когда мы смотрим, допустим, на ламинат с близкого расстояния, мы видим параллельные прямые, хотя они, вроде должны быть не параллельными в перспективной проекции. Я позволил себе небольшое отступление, вернемся к перспективной проекции.
Перспективу можно описать следующим образом – чем дальше объект, тем он меньше. Насколько объект удален от нас, зависит от координаты Z. Соответственно при удалении координаты x,y будут смещаться в центр, т.е. уменьшаться.
Вычислять новые координаты будем по следующие формуле:
x’ = x * F / (F + z)
где F – фокусное расстояние.
&НаКлиенте
Функция ПолучитьКоордиантыТочек(Объект, МатрицаПреобразований)
рТочки = Новый Массив();
Для Каждого Точка Из Объект.Точки Цикл
рТочка = Новый Массив(4);
рТочка[0] = Точка[0] * МатрицаПреобразований[0][0] + Точка[1] * МатрицаПреобразований[1][0] + Точка[2] * МатрицаПреобразований[2][0] + Точка[3] * МатрицаПреобразований[3][0];
рТочка[1] = Точка[0] * МатрицаПреобразований[0][1] + Точка[1] * МатрицаПреобразований[1][1] + Точка[2] * МатрицаПреобразований[2][1] + Точка[3] * МатрицаПреобразований[3][1];
рТочка[2] = Точка[0] * МатрицаПреобразований[0][2] + Точка[1] * МатрицаПреобразований[1][2] + Точка[2] * МатрицаПреобразований[2][2] + Точка[3] * МатрицаПреобразований[3][2];
рТочка[3] = Точка[0] * МатрицаПреобразований[0][2] + Точка[1] * МатрицаПреобразований[1][2] + Точка[2] * МатрицаПреобразований[2][2] + Точка[3] * МатрицаПреобразований[3][3];
рТочка[2] = рТочка[2] + 40;
//УголОбзора = 90;
//рТочка[0] = рТочка[0] * УголОбзора/рТочка[2] + 80;
//рТочка[1] = рТочка[1] * УголОбзора/рТочка[2] + 80;
ФокусноеРасстояние = 80;
рТочка[0] = рТочка[0] * ФокусноеРасстояние / (ФокусноеРасстояние + рТочка[2]) + 80;
рТочка[1] = рТочка[1] * ФокусноеРасстояние / (ФокусноеРасстояние + рТочка[2]) + 80;
рТочки.Добавить(рТочка);
КонецЦикла;
Возврат рТочки;
КонецФункции
Куб в начальной позиции.
Добавим преобразования поворот вокруг осей
Обработка тестировалась на программных файлах 1С:Предприятие 8.3 (8.3.12.1529), подключение - тонкий клиент.
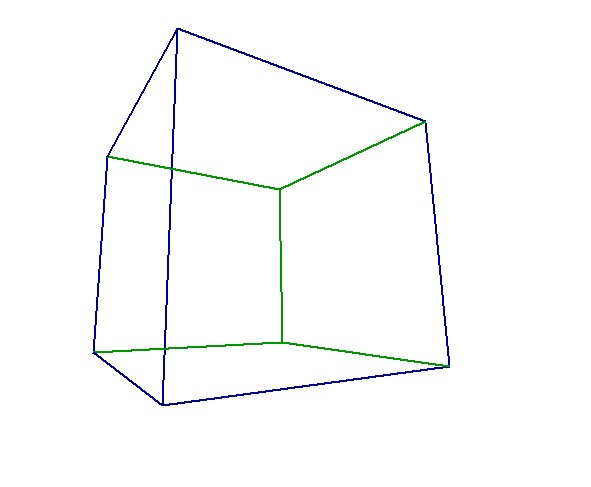
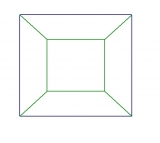
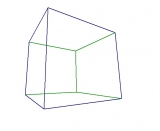
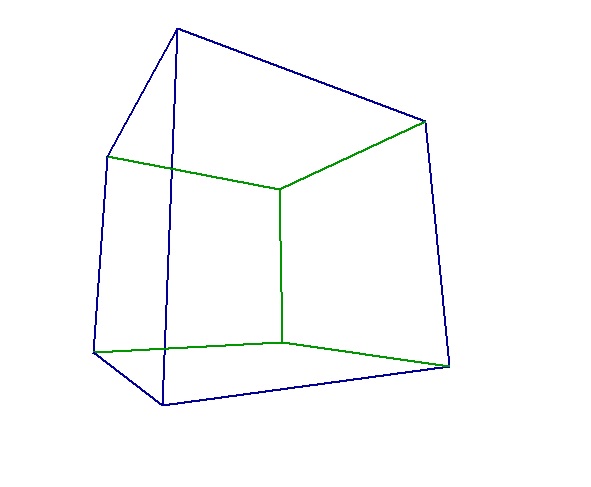Что вы сделали с кубом? Зачем так растянули и исказили его? Я имею в виду, очевидно что спереди находятся зелёные грани 
Это явно не куб, а что-то трапецевидное.
