Алгоритмы. Часть 1.1. Динамические соединения.

Алгоритмы – это методы решения проблем. Алгоритмы применяются практически в любой области человеческой деятельности. Умение составлять правильные и эффективные алгоритмы является важным качеством любого специалиста практически из любой области.

«Я считаю, что разница между плохим и хорошим программистом в том – считает ли он свой код или структуры данных более важными. Плохой программист заботится о коде. Хороший программист – о структуре данных и их взаимосвязях».
Линус Торвальдс

«Алгоритмы + структуры данных = программы».
Никлаус Вирт

Зачем изучать алгоритмы?

1. Они имеют очень широкое распространение и влияние.
2. Имеют глубокие корни и предоставляют широкие возможности.
3. Помогают решить проблемы, которые не могут быть решены иным путем.
4. Помогают стать хорошим программистом.
5. Они могут раскрыть секреты жизни и вселенной.
6. Для саморазвития, интеллектуальной стимуляции и хорошего заработка.

Лекция 1. Соединение-поиск.

Порядок преподнесения материала в лекциях:

1. Сформулировать проблему/задачу.
2. Найти алгоритм решения
3. Достаточно ли он быстр? Достаточно ли памяти?
4. Если нет – понять почему.
5. Найти пути оптимизации.
6. Повторить пока не будем удовлетворены результатом.

Так называемый Научный метод

Динамические соединения.

Допустим мы имеем массив из N объектов, а также 2 команды:
1. Процедура Объединить – создает соединение между двумя объектами.
2. Функция ОбъектыСоединены – проверяет наличие пути, который объединяет 2 объекта.

Пример задачи: существует ли путь, соединяющий точки p и q?
(поиск конкретного пути в данной лекции не рассматривается!)

Будем считать, что тезис «объект p соединен с объектом q» включает в себя следующие утверждения:

• p соединен с p, т.е. объединен сам с собой;
• если p соединен с q, то q соединен c p;
• если p соединен с q и q соединен с r, то p соединен с r.

Коллекция соединенных объектов – перечень всех объектов, объединенных в единую сеть.

Таким образом, операция проверки наличия пути между объектами сводится к проверке принадлежности 2 объектов одной коллекции. А операция объединения объектов – к объединению двух коллекций.

Для хранения информации о количестве объектов и их связях будем использовать одномерный массив, где индекс элемента будет равен порядковому номеру объекта, а значение – связью между объектами.

1 методика. Быстрый поиск.

Алгоритм, который обеспечит максимально быструю проверку наличия связи между двумя объектам.

Для реализации этого метода допустим, что в массиве будет храниться информация о принадлежности элемента к коллекции соединенных объектов. При этом идентификатором коллекции будет порядковый номер одного из элементов.

Например:

представлены 3 коллекции:

• 0, 5 и 6 – коллекция с индексом 0
• 1, 2 и 7 – коллекция с индексом 1
• 3, 4, 8 и 9 – коллекция с индексом 8

Логика работы операций:

ОбъектыСоединены(p, q) – проверить равенство идентификаторов у элементов с индексами p и q. Если идентификаторы равны – объекты соединены, иначе – нет.

Объединить(p, q) – объединить 2 коллекции – заменить у всех элементов идентификаторы q на p.

Например, выполним объединение объектов 6 и 1 (помимо 6 необходимо переподчинить объекты 0 и 5, т.к. они были связаны с 6):

И сразу видим проблему – пришлось изменить идентификаторы у большого числа объектов.

Затраты. Число операций чтения и записи для массива размером N:

При этом операция объединения слишком затратная. Она требует N^2 доступов к массиву для выполнения последовательности из N команд для N объектов.

Алгоритм получился квадратичным. А квадратичные алгоритмы не масштабируются, даже с учетом развития технологий.

Грубый пример: процессор выполняет 10^9 операций в секунду, для доступа к 10^9 объектам в памяти требуется 1 секунда. Но для выполнения 10^9 команд объединения по алгоритму быстрого поиска потребуется более 10^18 операций. Более 30 лет компьютерного времени.
Можно взять компьютер в 10 раз более производительный, но в 10 раз большая задача будет решаться в 10 раз медленнее!

Реализация в 1С:

См. обработку «БыстрыйПоиск»

2 методика. Быстрое объединение.

Алгоритм, который обеспечит максимально быстрое объединение двух объектов.

В этом случае изменим схему хранения связей - в значениях массива будут храниться индексы ближайших связанных объектов: id[i] это родитель для i.
А для вычисления корня потребуется рекурсия id[id[id[...id[i]...]]]

Логика работы операций:

ОбъектыСоединены(p, q) – проверить что элементы с индексами p и q имеют один и тот же корень.

Объединить(p, q) – добавить корневой элемент первой коллекции к корневому элементу второй коллекции.

Например, выполним объединение объектов 3 и 5:

Затраты. Число операций чтения и записи для массива размером N:

Дефекты быстрого поиска:

• Объединение слишком затратно
• Деревья плоские, но слишком затратно поддерживать их таковыми

Дефекты быстрого объединения:

• Деревья бывают очень высокими
• Поиск слишком затратен.

Реализация в 1С:

См. обработку «БыстроеОбъединение»

Первое улучшение. Оценка веса.

Быстрое объединение с оценкой веса деревьев:

1. Изменить предыдущий алгоритм там, чтобы избегать высоких деревьев.
2. В отдельной структуре хранить размеры каждого дерева
3. При объединении деревьев всегда присоединять малое дерево к корню большого (метрика рассчитывается исходя из числа узлов в дереве).

Пример результатов работы обоих методов:

Скорость выполнения операций объединения и проверки соединения в данном случае пропорциональна длине веток. Длина веток при этом не превосходит lg N.

Затраты. Число операций чтения и записи для массива размером N:

Реализация в 1С:

См. обработку «БыстроеОбъединениеСОценкойВеса»

Второе улучшение. Сжатие пути.

Быстрое объединение со сжатием пути:

1. При каждом вычислении корня выполним привязку всех глубоко вложенных объектов к корню.
2. Это потребует только 1 дополнительную строку кода!

Например, для данного дерева при вычислении корня для объекта номер 9 будет выполнен перенос объектов 9, 6 и 3 к верхнему уровню.

Исходное дерево:

Результат:

На практике – нет причин не использовать этот метод. Он позволяет поддерживать дерево плоским.

Реализация в 1С:

См. обработку «БыстроеОбъединениеСоСжатиемПути»

Финальный вариант. Быстрое объединение с оценкой веса и сжатием пути.

Утверждение (Hopcroft-Ulman, Tarjan): начиная с пустой структуры данных любая последовательность операций объединения-поиска M для N объектов потребует =< c ( N + M lg* N ) числа доступов к массиву.

Где ln*N:

Итог.

Быстрое объединение с оценкой веса и сжатием пути позволяет решить задачи, которые не могут быть решены иным путем.

Где M – число операций объединения и проверки соединения для массива из N-объектов.

Последний вариант позволяет сократить время решения задачи с 30 лет до 6 секунд.
Суперкомпьютер сильно не поможет, а качественный алгоритм даст решение.

Графики времени выполнения алгоритмов в 1С.
Все 5 вариантов:

Без 1 и 2 варианта:

Пример применения алгоритма – вычисление проницаемости структуры.

Модель для множества физических систем:

1. Фигура размером N*N из объектов
2. Каждый объект является либо открытым (проницаемым) с вероятностью p, либо закрытым (непроницаемым) с вероятностью 1-p.
3. Система проницаема только в том случае, если любой объект из верхнего ряда соединен с любым объектом из нижнего ряда

Зависимость проницаемости структуры от вероятности проницаемости каждого объекта (p).

При большом числе N теория гарантирует наличие четкого порога p*, при котором:

• если p > p* - структура почти наверняка проницаема
• если p < p* - структура почти наверняка непроницаема.

p* получено путем симуляции на больших массивах данных и не доказано математически:

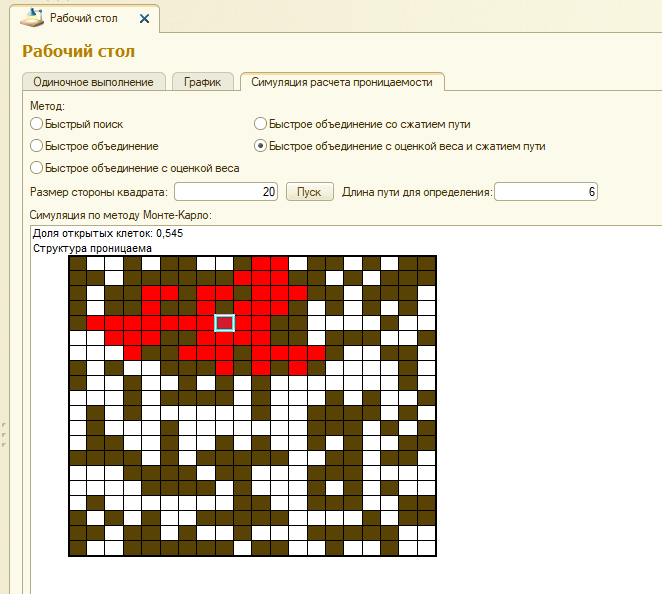
Симуляция по методу Монте-Карло для вычисления p*.

http://ru.wikipedia.org/wiki/%CC%E5%F2%EE%E4_%CC%EE%ED%F2%E5-%CA%E0%F0%EB%EE

1. Создать структуру N*N из закрытых клеток.
2. Последовательно и случайно открывать закрытые клетки до тех пор, пока верхний ряд не будет соединен с нижним рядом.
3. Процент открытых клеток даст значение p*

Применение алгоритма динамических соединений для определения проницаемости структуры.

1)      Создать структуру N*N и последовательно определить для каждой клетки элемент в массиве:

2)      Выполнить объединение соседних открытых клеток:

3)      Структура будет проницаемой, если любой объект из верхнего ряда соединен с любым объектом из нижнего ряда. Для упрощения проверки добавим виртуальные вершины для верхнего и нижнего ряда. Проверка будет сведена к единственной операции проверки связи между двумя вершинами:

Симулируем открытие случайной клетки. Необходимо проверить всех «соседей» и выполнить соединение с теми из них, которые уже открыты.

Во вложенной конфигурации 1С приведена реализация данного подхода.

P.S. - если обнаружите нестыковки, ошибки - пишите в комментариях, я поправлю.