Основными измеримыми показателями алгоритмов являются сложность и расход памяти. На расходе памяти останавливаться отдельно не будем, поскольку тут все довольно интуитивно понятно: чем больше промежуточных данных мы вынуждены создать в ходе работы алгоритма - тем больше расход, а вот про сложность стоит поговорить подробнее.
Итак, сложность алгоритма - это показатель зависимости роста времени выполнения программы от количества входных данных. Иными словами, насколько вырастет число итераций некоторых действий при росте числа входных данных. При этом абсолютное время каждого конкретного действия в данной концепции значения не имеет, поскольку это скорее всего какой-то внешний параметр, на который конкретный алгоритм не имеет никакого влияния. Имеет значение только, как быстро растет количество повторений.
Тут можно подумать: что за ерунда? Если надо обработать массив из 10 элементов - надо выподнить что-то 10 раз. Если из 100 элементов - 100 раз, как может быть иначе?
Может. Рассмотрим на примере. Всем изместный алгоритм пузырьковой сортировки выглядит как двойной цикл, примерно так:
Для и1 = 0 По Массив.ВГраница() Цикл
Для и2 = 0 ПО Массив.ВГраница() Цикл
...
Тут несложно увидеть, что c ростом размера массива - количество итераций цикла будет расти с квадратичной зависимостью: на каждый новый элемент массива в "верхем" цикле мы обойдем весь массив еще раз в нижнем цикле. На графике это будет выглядеть так:
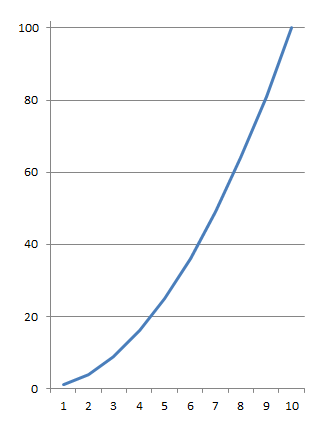
похоже на параболу.
Если массив имеет 4 элемента - цикл выполнится 16 раз. Если 5 - 25, 6 - 36 и т.д. Это называется квадратичной сложностью. На самом деле есть оптимизации позволяющие сократить это время более чем вдвое, чтобы формула сложности выгляделя так: n²/2 - n/2, но поскольку мы говорим не о каких-то точных значениях, а об оценке алгоритма и фрагмент n² тут доминирует над остальными операциями, всей остальной частью формулы обычно пренебегают и говорят, что сложность алгоритма пузырьковой сортировки - n². Записывают обычно в таком виде: O(n²), это называется "нотация большого О".
В разработке прикладных решений понимание того факта, какой сложносьтю обладает разработанный алгоритм не всегда нужно, поскольку высокая (квадратичная или даже выше) сложность обычно нивелируется небольшим количеством обрабатываемых данных и высокой производительостью серверов в энтерпрайзе. Ну какое количество строк может быть в накладной? 50? 100? 500? Алгоритм с квадратичной зависимостью на 10 строках будет иметь 100 итераций, а на 100 - 100 тысяч. Казалось бы колоссальный рост, но если выражать его в секундах - то на хорошем Xeon мы выросли с 0,0005 до 0,5 секунды - кому это будет интересно на фоне того сколько он будет проводиться? Ну документ большой, работает долго, подумаешь..
Но!
Во-первых, строк не всегда 500. Если вы имеете дело с каким-нибудь хитрым алгоритмом анализа остатков или распределения товаров, где, например, 25 тысяч товаров умножаются на 300 магазинов - строк уже не много не мало 7,5 миллионов. Каждая новая строка в таком случае будет добавлять 7,5 миллионов итераций, что уже, согласитесь существенно. Тут стоит всеми правдами и неправдами стараться перестроить алгоритм так, чтобы вместо одного вложенного цикла, дающего сложность O(n²), у нас было 2,3,4 обычных цикла, дающих сложность O(2n), O(3n), O(4n) соответственно. Как добиться такой замены - отдельный вопрос, это не всегда возможно (например пройти первый раз - построить индекс - пройти второй раз с поиском не перебором, а по индексу с логарифмической сложностью), но если возможно - делать стоит однозначно. На следующем графике приведен рост временивыполнения алгоритмов O(n), O(4n) и O(n2):
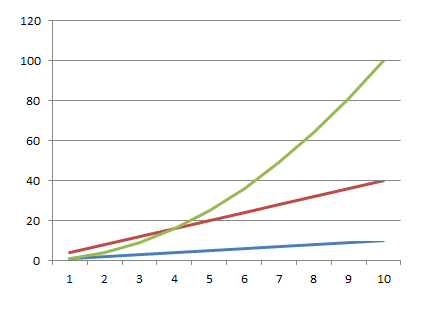
обратите внимание, тут всего 10 элементов на входе, если будет больше - линейные алгоритмы просто не оторвутся от оси на фоне роста квадратичного.
Во-вторых, зависимость не всегда квадратичная. Если так случится, что вы зачем-то вложите 3-й цикл (не вспомню конкретных задач, но я такое встречал и даже писал), зависимость уже будет кубической, а она растет еще быстрее. Чтобы проиллюстрировать это - сведем на одном графике линейную, квадратичную и кубическую зависимость.
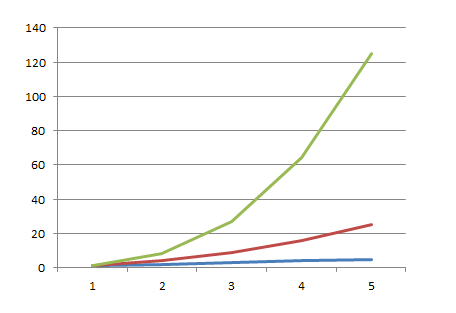
на этом графике всего лишь 5 элементов по той же причине.
На самом деле, хитрые компьютер-саенс специалисты для большинства типичных операций имеют алгоритмы лучше чем квадратичной сложности. Как правило, алгоритм обработки большого объема данных обходитя в log(n), а в некоторых случаях вообще обходится константной сложностью (это когда время выполнения вообще не зависит от объема данных). Все алгоритмы сортировки, поиска и т.п. так умеют. Достигается это иногда при помощи улучшения самого алгоритма, иногда построения хитрых индексных или хэш- таблиц, но достигается всегда. Почти ). Поэтому когда вы реализуете алгоритм, обладающий квадратичной или хуже сложностью - задумайтесь: не стоит ли его оптимизировать?
Вступайте в нашу телеграмм-группу Инфостарт