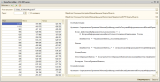
Считать ли злом копирование фрагментов кода (копипаст) в процессе программировании на 1С – решайте сами. Есть другой интересный вопрос – как найти и измерить копипаст в уже написанной программе. Одна из возможностей - использование предлагаемого отчета.
Перед использованием отчета тексты программных модулей анализируемой конфигурации необходимо выгрузить в некоторую папку. Это можно сделать через конфигуратор с использованием пункта меню "Конфигурация\Выгрузить файлы конфигурации". Далее можно запустить формирование отчета, указав ту папку, в которую были выгружены файлы. Через несколько минут (время зависит от общего числа строк в программных модулях) отчет покажет список повторов в виде таблицы, каждая запись которой содержит размер повторяющегося фрагмента в строках, место фрагмента и его копии в сквозной нумерации строк всех модулей. Выделив конкретный повтор в списке, можно увидеть сам фрагмент, имя содержащего его модуля и номер строки начала фрагмента в данном модуле, а также имя модуля и номер строки копии фрагмента.
Применив отчет к некоторым типовым конфигурациям, можно увидеть, что например, в 1С: Бухгалтерии 2.0 общее число строк всех модулей конфигурации превышает 3,5 миллиона (на их анализ ушло порядка 20 минут). При этом имеется очень большое количество повторений фрагментов. В основном повторяются тексты модулей в регламентированной отчетности. Длина цельнотянутых кусков достигает 10 тысяч строк! А повторение тысячи строк в этой подсистеме - вообще норма. В других подсистемах также можно встретить очень большие повторяющиеся куски. Впрочем, лучше один раз увидеть, чем сто раз услышать: смотрите и удивляйтесь!
Несколько слов о реализации.
Основная идея метода - использование LCP-массива, который строится по конкатенации текстов модулей анализируемой конфигурации.
Формирование отчета состоит из этапов:
- Чтение текстов модулей. При этом строки модулей получают сквозную нумерацию в массиве "Ранг", запоминаются размеры модулей (чтобы потом можно было восстановить имя модуля и номер строки в нем), сама строка обрезается от пробелов слева и справа и получает ранг, равный количеству различных строк, встреченных в текстах модулей ранее. Таким образом, все разные строки обозначаются в массиве "Ранг" разными числами от нуля до старшего номера.
- Построение суффиксного массива. Входной строкой при этом считается последовательность элементов массива "Ранг". Здесь используется алгоритм, изобретенный в 1993 году Манбером (сейчас вице-президент Гугла) и Майерсом. Особенности данной реализации в том, что строка для удобства зациклена (адресуется по модулю длины строки), а не дополнена сентителами справа. А также в том, что раскладка по корзинам осуществляется с использованием такой структуры данных языка 1С, как массив массивов. При этом первый элемент каждого вложенного массива хранит предыдущий символ, положенный в соответствующую корзину. Смена символа отмечается добавлением к номеру нового символа одной десятой (чтобы не тратить на это дополнительную память). Далее массив "Ранг" обходится "змеей": во внешней цикле по корзинам и во внутреннем цикле - по содержимому корзин и заново нумеруется. Порядок обхода задается следом змеи, а сдвиг (охват) между обрабатываемым символом и корзиной увеличивается каждый раз вдвое, пока все символы в массиве «Ранг» не кажутся разными. Вот код процедуры построения суффиксного массива:
Процедура ПолучитьСуффиксныйМассив_(Ранг, След, Охват = 1) Экспорт Старший = След.ВГраница(); К = Ранг.Количество(); Пока Старший < Ранг.ВГраница() Цикл Змея = Новый Массив(Ранг.Количество(), 1); Для у = 0 По След.ВГраница() Цикл Для ж = 1 По След[у].ВГраница() Цикл ё = (Цел(След[у][ж]) - Охват + К) % К; х = Ранг[(ё + Охват) % К]; Змея[Ранг[ё]].Добавить(ё + 0.1 * (Змея[Ранг[ё]][0] <> х)); Змея[Ранг[ё]][0] = х КонецЦикла КонецЦикла; Старший = - 1; Для у = 0 По К - 1 Цикл Для ж = 1 По Змея[у].ВГраница() Цикл ё = Змея[у][ж]; Старший = Старший + ё % 1 * 10; Ранг[ё] = Старший КонецЦикла КонецЦикла; Охват = Охват * 2; След = Змея КонецЦикла КонецПроцедуры
- Построение LCP-массива. LCP-массив показывает для каждого символа строки (это каждая строка программы в нашем случае) длину наибольшего общего префикса для подстроки, начинающейся в данном месте, и подстроки, следующей за ней в суффиксном массиве. Буквально это и есть длина наибольшего повторяющегося фрагмента, начинающегося в данном месте. Небольшая деталь заключается в несимметричности связи этих одинаковых фрагментов, которая в данном случае оказывается даже выгодной. Поскольку найденная копия окажется в суффиксном массиве позже, то для нее уже не будет копией текущий фрагмент. Поэтому каждый фрагмент будет встречаться в выдаче алгоритма только один раз. Построение LCP-массива выполняется по алгоритму Касаи. Вот код процедуры построения LCP-массива:
Процедура ПолучитьДлиныНаибольшихОбщихПрефиксов_(Тень, Ранг, Путь, Рост, Плюс = 0) Экспорт Для ё = 0 По Ранг.ВГраница() Цикл Путь[Ранг[ё]] = ё КонецЦикла; Для ё = 0 По Ранг.ВГраница() Цикл ж = ?(Ранг[ё] < Ранг.ВГраница(), Путь[Ранг[ё] + 1], Ранг.Количество()); Пока Макс(ё, ж) + Плюс < Тень.Количество() И Тень[ё + Плюс] = Тень[ж + Плюс] Цикл Плюс = Плюс + 1 КонецЦикла; Рост[ё] = Плюс; Плюс = Макс(0, Плюс - 1) КонецЦикла КонецПроцедуры
- Выделение повторов из LCP-массива. Если представить LCP-массив графиком, то интерес для отображения повторов будут иметь только зубцы этого графика, поскольку другие точки будут соответствовать меньшим по размеру повторам, полностью входящим в бОльший по размеру повтор слева (сверху). Наибольшие повторы отбираются простейшим алгоритмом сравнения текущего значения со значениями слева и справа. При этом в отчете можно задать порог, чтобы не выбирались повторы, число строк в которых меньше этого порога. Вот код выделения повторов:
Функция ОтборМестПовторов_(Ранг, Путь, Рост) Экспорт Ответ = Повторы.ВыгрузитьКолонки(); Для ё = 0 По Рост.ВГраница() Цикл у = Макс(0, ё - 1); ж = Мин(ё + 1, Рост.ВГраница()); Если Порог < Рост[ё] И Рост[у] <= Рост[ё] И Рост[ё] >= Рост[ж] Тогда э = Ответ.Добавить(); э.Место = ё; э.Рост = Рост[ё]; э.Копия = Путь[Ранг[ё] + 1] КонецЕсли КонецЦикла; Возврат Ответ КонецФункции
- И, наконец,повторы сортируются в порядке убывания их размеров.
Выводы
- Правильно выбранный алгоритм может скомпенсировать недостаточное быстродействие платформы 1С при проведении быстрых массовых вычислений без необходимости применения внешних компонент.
- В данной задаче не усматривается необходимости применения более сложных алгоритмов построения суффиксного массива (типа алгоритма Каркайнена – Сандерса и других), так как для разовых применений быстродействия алгоритма достаточно.
- Структуры данных платформы 1С позволяют получать компактный и выразительный код при реализации самых хитрых алгоритмов.
- Подход,положенный в основу данного отчета, может послужить основой и для более изощренных методов обработки текстов программ. С его помощью можно искать часто встречающиеся полезные шаблоны (оставив в анализируемых текстах только ключевые слова или канонизировав тексты модулей другим способом). Можно автоматически выносить повторяющиеся функции и процедуры в общие модули. Можно искать зависимости при внесении изменений в конфигурации. И так далее.
- Приведенные алгоритмы – это совсем небольшая (и довольно простая) часть алгоритмов над строками. Имеющих, кроме показанных в данном отчете, множество других применений. Например, на основе суффиксного массива часто строится индекс, используемый при полнотекстовом поиске. Знание этих алгоритмов позволяет эффективно решать и многие другие практические задачи.
- Ну и остался загадкой вопрос: есть ли какие-либо фундаментальные причины у большой избыточности текстов программ типовых конфигураций, замеченной с помощью предлагаемого отчета, или играют роль организационный и человеческий факторы?
Ссылки
- Суффиксный массив — удобная замена суффиксного дерева http://habrahabr.ru/post/115346/
- MANBER U., MAYERS G.. Suffix arrays: a new methodfor on-line string searches // SIAM Journal on Computing. – 1993. – №22. – P.953–948.
- http://en.wikipedia.org/wiki/Suffix_array
- Kasai, T.; Lee, G.; Arimura, H.;Arikawa, S.; Park, K. (2001). "Linear-Time Longest-Common-PrefixComputation in Suffix Arrays and Its Applications". Proceedings ofthe 12th Annual Symposium on Combinatorial Pattern Matching. LectureNotes in Computer Science 2089. pp. 181–192. doi:10.1007/3-540-48194-X_17. ISBN 978-3-540-42271-6.
Вступайте в нашу телеграмм-группу Инфостарт