Сегодня у нас тема для довольно долгого и, надеюсь, интересного разговора - метода имитации отжига.
Сам метод является подвидом более общего метода поиска решения, известного под названием "метода Монте-Карло". Как и любой стохастический метод, имитация отжига не гарантирует нам наилучшего решения, но в дополнение к этому данный метод не гарантирует нам получение даже наилучшего решения среди рассмотренных. Такая вот довольно на первый взгляд непрактичная штуковина. Однако, как учит нас диалектика, всегда есть "но". Это "но" в данном случае - хороший шанс выбраться из "локального минимума". Еще одним несомненным достоинством данного метода является простота реализации. Ну а для того, чтобы Вам было действительно просто его реализовать, давайте попытаемся разобраться с тем, что такое отжиг, для чего он нужен и как это все, собственно, работает.
Отжиг - термин из металлургии. Это процесс термической обработки металла для увеличения его прочности на разрыв и сдвиг или повышения пластичности и снижения хрупкости. Суть процесса в том, что металл подвергают нагреванию, выдерживают определенное время при температуре рекристаллизации, а затем медленно охлаждают. Дело в том, что кристаллическая структура металла не идеальна и имеет большое количество деформаций (дефектов и дислокаций), нарушающих оптимальное позиционирование атомов вещества. В процессе отжига атомы набирают энергию, достаточную для изменения положения в металлическом кристалле, и начинают распределяться по позициям равновесия. По мере остывания металла энергия для перемещений утрачивается, и переходы атомов в новые позиции становятся все реже, а длина переходов все короче, пока в конце концов заготовка не стабилизируется на новой кристаллической структуре. В ходе отжига структура металла избавляется от значительного числа деформаций, энергетических дисбалансов и напряжений становится меньше и металл оказывается прочнее и пластичнее, чем до отжига. Вот, собственно, этот процесс и моделируется методом имитации отжига.
Теперь выделим основные черты отжига, которые необходимо смоделировать при поиске решения:
1. Очевидно, что процесс перемещения атомов носит при отжиге случайный характер, а это значит, что каждое новое состояние вещества (решения) должно быть одновременно связано с предыдущим состоянием и в то же время быть результатом случайного перемещения случайного количества случайных атомов из предыдущего состояния.
В алгоритме метода это имитируется любой функцией, производящей случайные модификации во временном решении. Назовем такое решение - возможным решением.
2. Атомы стремятся занять в кристаллической решетке положения с наибольшей энергией связи и наименьшей энергией отталкивания, а это значит, что переход из лучшего состояния в худшее менее вероятен и вероятность этого перехода тем меньше, чем меньше имеется энергии на разрыв сил притяжения у атомов. Или, попросту говоря, чем ниже температура и чем дальше состояние от оптимального, тем сложнее веществу перейти в это состояние.
Метод имитации отжига в данном случае сравнивает текущее и возможное решения по критерию оптимизации и, если возможное решение лучше, - оно становится текущим, то есть система нашла лучшую структуру вещества и перешла в новое состояние. В противоположном случае вычисляется вероятность перехода в худшее состояние как функция, обратно зависящая от того, насколько хуже стало новое состояние, и прямо зависящая от текущей температуры. Чем хуже новое состояние и чем ниже температура материала, тем ниже вероятность перейти в это состояние.
3. Температура должна снижаться постепенно и достичь значения, при котором движение атомов полностью прекращается. Это и будет означать окончание процессов отжига и поиска решения.
Температура моделируется любой монотонно убывающей функцией. Главное, чтобы процесс "остывания" шел достаточно долго, поэтому показательные функции в данном случае не совсем уместны. В металлургии техрегламенты отжига предусматривают равномерное снижение температуры в градусах в минуту, поэтому, имитируя реальный отжиг, лучше воспользоваться линейной функцией.
Теперь введем несколько обозначений:
Х - множество значений переменных, составляющих возможное решение задачи оптимизации.
Z(X) - целевая функция, которую возможно рассчитать для любой совокупности Х. Оптимальное решение будет означать минимум данной функции.
Tmax и Tmin - максимальная и минимальная температуры отжига.
Frand(Xi) - функция случайного преобразования решения Xi. Функция произвольная и теоретически должна выбираться с учетом специфики задачи, но на практике замена случайных переменных новыми случайными значениями дает вполне приличный результат. Количество изменяемых на случайные (инвертируемых) переменных также выбирается произвольно. Для гибкости я сделал интенсивность инверсии одним из параметров функции поиска решения.
N - количество итераций поиска решения (длительность отжига).
И под конец распишем алгоритм по шагам:
1. Формируем начальное решение, инициируя Хi случайными значениями. i=0.
2. Устанавливаем температуру.
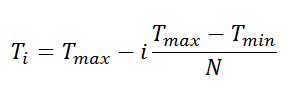
3. Если Тi>Tmin продолжаем. Иначе возвращаем Xi.
4. Вычисляем возможное решение Х*
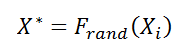
3. Находим
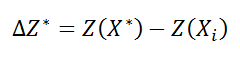
5. Определяем Xi+1. В зависимости от значения ΔZ и текущей температуры вероятность того, что Xi+1 будет равно Х*, выражается формулой:
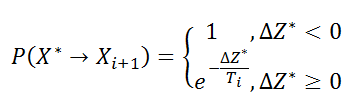
Определяем, переходит ли Х* в Хi+1, бросая монетку. То есть генерируем случайное число от 0 до 1 и сравниваем с вероятностью Р. Если случайное число превысило или равно Р - переход произошел, и мы присваиваем Xi+1=X*, если же Х* не перешло в Хi+1, тогда присваиваем Xi+1= Xi.
6. Увеличиваем счетчик итераций i=i+1. Переходим к шагу 2.
Единственное, что хочется пояснить - это пункт 5 алгоритма. А точнее, формулу ![]() вероятности того, что следующее текущее решение будет хуже предыдущего. Если вспомнить математику, то становится понятным, что дробь тем меньше, чем меньше числитель и чем больше знаменатель, и именно при значениях показателя дроби близких к 0 вероятность перехода к новому решению будет максимальна и близка к 1. Как видим, эта вероятность тем выше, чем меньше разница между оценками целевой функции и чем выше текущая температура. При больших (по модулю) значениях отрицательного показателя степени вероятность перехода к возможному решению стремится к нулю. Например, для числа е показатель по модулю больше пяти дает практически нулевую вероятность того, что система перейдет в новое, менее оптимальное состояние.
вероятности того, что следующее текущее решение будет хуже предыдущего. Если вспомнить математику, то становится понятным, что дробь тем меньше, чем меньше числитель и чем больше знаменатель, и именно при значениях показателя дроби близких к 0 вероятность перехода к новому решению будет максимальна и близка к 1. Как видим, эта вероятность тем выше, чем меньше разница между оценками целевой функции и чем выше текущая температура. При больших (по модулю) значениях отрицательного показателя степени вероятность перехода к возможному решению стремится к нулю. Например, для числа е показатель по модулю больше пяти дает практически нулевую вероятность того, что система перейдет в новое, менее оптимальное состояние.
С другой стороны, возможность переходов к худшим решениям, особенно при высокой температуре основное достоинство алгоритма, так как мы можем "выпрыгивать" из локальных минимумов и искать новые. По мере "остывания" перейти к сильно уж далекому от текущего оптимума решению становится все сложнее, но мы предполагаем, что, "прыгая", пока было "горячо", мы нашли самую глубокую яму, и теперь снижение температуры только фиксирует нас в ней, не давая уйти совсем из окрестностей глобального минимума, но позволяет последовательно улучшать решение в окрестностях этого минимума.
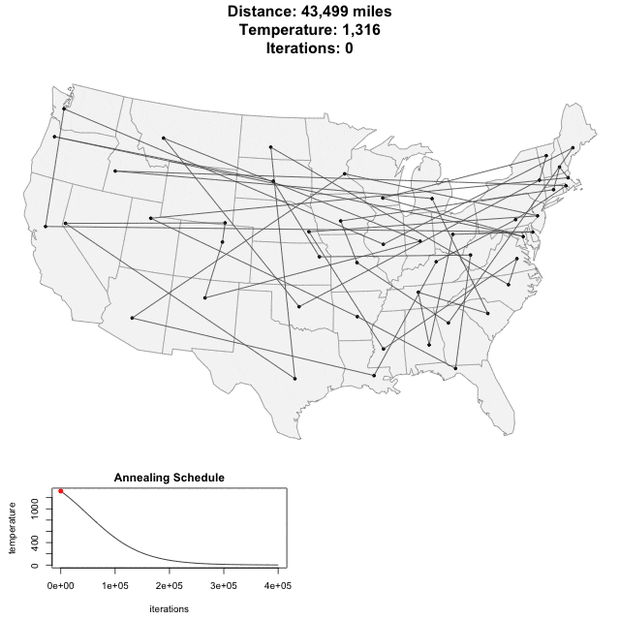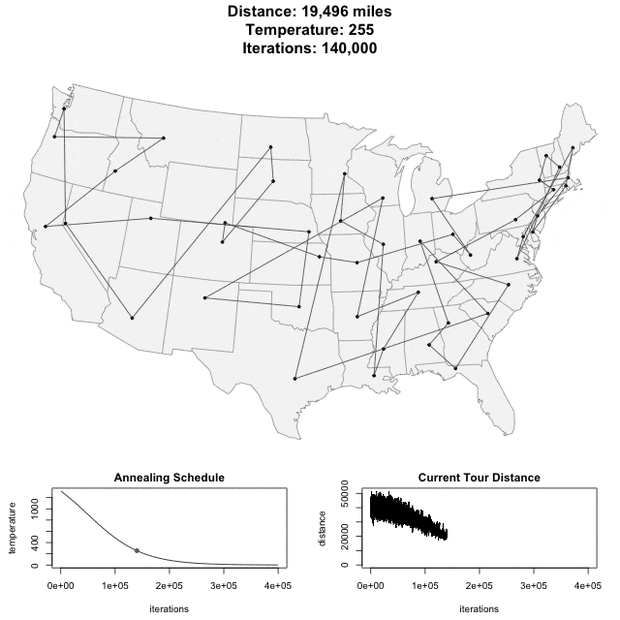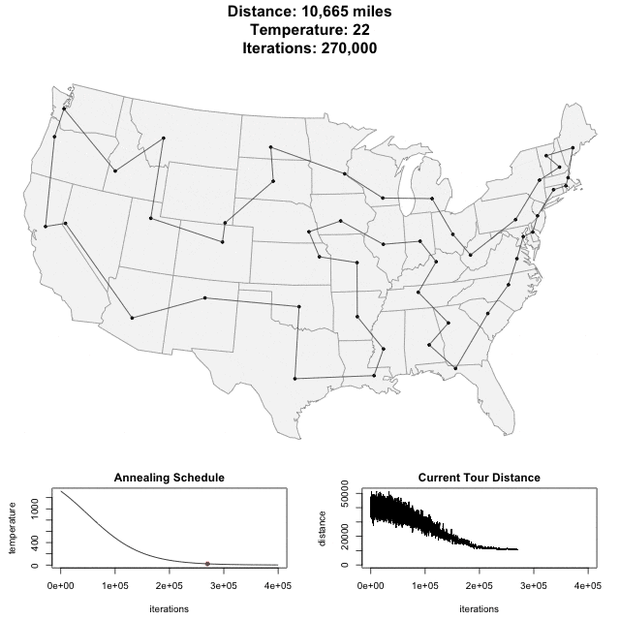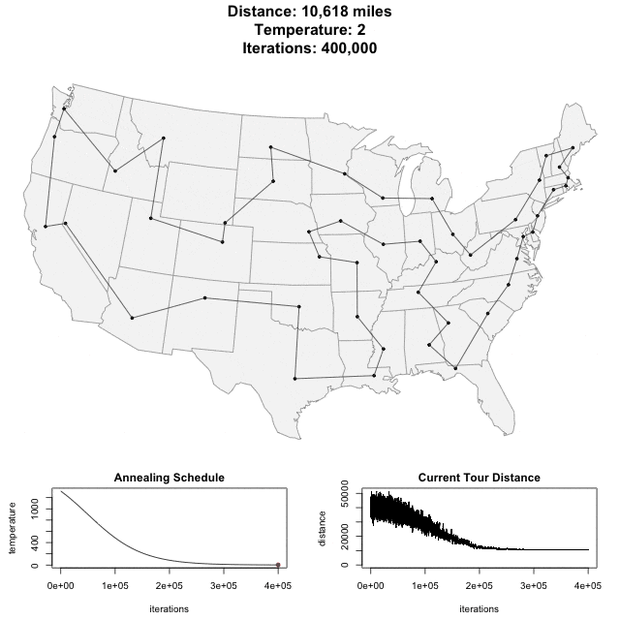
Для демо примера я взял обработку из прошлой публикации про генетический алгоритм, добавив возможность решать ту же задачу коммивояжера методом имитации отжига. Получилось, что примерно за одинаковое время эти два метода решения дают примерно одинаковый по качеству результат. Впрочем, оценить все на месте и сформировать свое мнение Вы можете и сами.
И под конец гифка о том, как решается задача коммивояжера методом имитации отжига на карте США.
Вступайте в нашу телеграмм-группу Инфостарт