Несмотря на определенную «заумность» термина, транзитивное замыкание – это простое и часто встречающееся на практике понятие. Вот примеры:
- Если известно, что пункт А связан с пунктом Б, а пункт Б с пунктом В, то делая вывод о том, что пункт А в итоге связан и с пунктом В, мы «транзитивно замыкаем» отношение «связанность».
- Если группа 1-1-1 входит в отдел 1-1, а тот, в свою очередь является частью департамента 1, то группа 1-1-1 также входит и в департамент 1 в результате «транзитивного замыкания» отношения «вхождение».
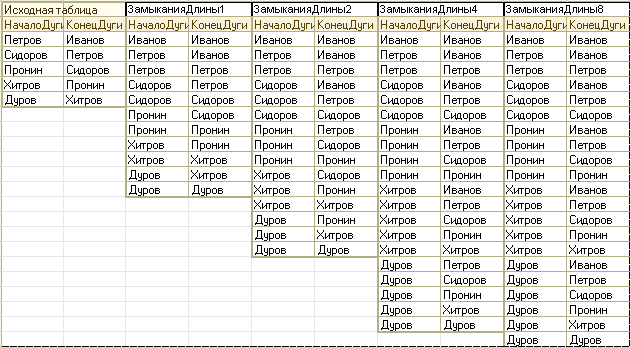
- Если рядовой Иванов подчиняется лейтенанту Петрову, лейтенант Петров – капитану Сидорову, капитан Сидоров – майору Пронину, майор Пронин – полковнику Хитрову, а полковник Хитров – генералу Дурову, то рядовой Иванов, хотя и закончил мехмат, также подчиняется генералу Дурову в результате транзитивного замыкания отношения «подчинение».
Получается, что когда спрашивается, как определить все группы, в которые входит некоторая номенклатура или как для каждого подразделения определить все подразделения, включенные в него иерархически, на самом деле необходимо решить одну и ту же математическую задачу: построить транзитивное замыкание соответствующих отношений.
Вопрос о том, как решать и можно ли вообще решить подобную задачу, встречается довольно часто. Можно упомянуть публикации "Получение родителя верхнего уровня с помощью СКД"[//infostart.ru/public/84547/], "Соединение в запросе, сравнение (В ИЕРАРХИИ)"[//infostart.ru/public/102086/], "Пример получения в запросе всех подразделений с учётом иерархии (неограниченный уровень вложенности подразделений)" [//infostart.ru/public/117349/], недавнее обсуждение на форуме "Запрос из справочника с выборкой подчиненных элементов" [http://forum.infostart.ru/forum26/topic72977/message781790/#message781790]. Решение, описываемое в статье, появилось в ходе обсуждения "Реально написать хитрый запрос" [http://forum.infostart.ru/forum14/topic35991/message395140/#message395140], и было там же опубликовано [(103)], однако осталось почти незамеченным. Данная публикация восполняет этот пробел.
Очевидная трудность решения данной задачи заключается в природе табличного представления отношений в реляционных СУБД. Допустим, отношения связанности (например) хранятся в таблице, которая имеет следующий вид:
| Пункт ... связан | с пунктом ... |
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
| ... | ... |
| 99 | 100 |
Тогда, чтобы определить, что пункт 1 связан с пунктом 100, потребуется выполнить множество соединений, число которых, к тому же, будет зависеть от исходных данных.
Тем не менее, решение есть. Оно довольно простое, хотя и не очевидное. Решение опирается на кое-какую математику. Вот она:
Если А – матрица смежности графа исходного отношения, то ее элемент aij равен 1, если i связан с j и 0, если связи нет. Таким образом, ненулевые элементы матрицы А фактически отмечают существование в отношении путей длины 1, А2 (А в степени 2) – путей длины 2, А3 – путей длины 3 и так далее. Если Е – единичная матрица, то
(А + Е)n = Аn + … + A3 + A2 + A + E.
Это специфическое биноминальное разложение представляет собой матрицу смежности графа, содержащего пути длины 0, 1, 2, 3, … , n. Здесь нет биноминальных коэффициентов, потому что операции умножения и сложения выполняются по правилам алгебры логики: 0+0=0, 0+1=1, 1+0=1, 1+1=1. Ну и поскольку в графе из N вершин нет путей длины больше N, то (A + E)N и будет матрицей смежности транзитивного замыкания исходного отношения.
Во всем, что говорилось до настоящего момента, ничего нового нет. Формулы выражают общеизвестный способ, когда мы по шагам накапливаем замыкание, добавляя на каждом шаге более длинные пути. То есть, в случае отношения иерархического подчинения, сначала находим и добавляем к итоговой таблице таблицу потомков уровня 1, потом уровня 2, потом уровня 3 и так далее.
Новое заключается в том, что:
- Замечено, что если M > N, где N – максимальная длина пути, то (A + E)N = (A + E)M. То есть, можно не бояться возведения в степень «с запасом», которая больше, чем максимальная длина пути (глубина иерархии). Результат от этого не изменится.
- Предлагается вычислять (A+E)M следующим быстрым и эффективным способом: (А+E)2 = (А+E)(А+E), (А+E)4 = (А+E)2 (А+E)2 , (А+E)8 = (А+E)4( А+E)4, (А+E)16 = (А+E)8( А+E)8 и так далее, пока степень не станет больше требуемой.
Если попытаться объяснить прием словами, без формул, то получится следующее:
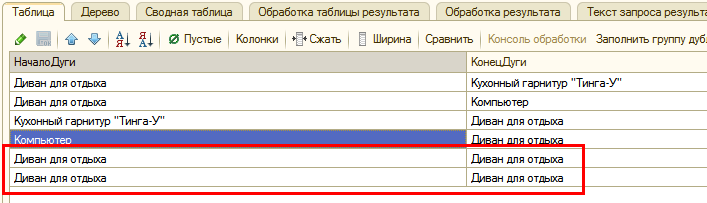
На первом этапе объединяем (UNION) с исходной таблицей путей длины 1 таблицу путей длины 0 (каждый элемент связан с самим собой). Далее соединяем (JOIN) эту таблицу с собой, чтобы получить в результирующей таблице пути длины 0, 1 и 2. Снова соединяем полученную таблицу с собой и получаем в результирующей таблице пути длины 0, 1, 2, 3, 4. Уже в следующем соединении получим пути длины 0, 1, 2, 3, 4, 5, 6, 7, 8. Далее максимальная длина пути будет быстро расти и очень скоро преодолеет любой заданный предел.
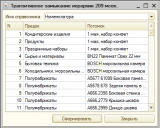
При реализации на языке 1С, получается следующая достаточно компактная функция, возвращающая в качестве результата таблицу транзитивного замыкания. Функция приведена на примере отношения иерархии групп и элементов справочника. Эту функцию можно использовать как шаблон и для других отношений. Потребуется всего лишь заменить текст в переменной «Пролог».
Функция ТранзитивноеЗамыкание(ИмяСправочника, МаксимальнаяДлинаПути) Экспорт
Пролог = "ВЫБРАТЬ Родитель НачалоДуги, Ссылка КонецДуги ПОМЕСТИТЬ ЗамыканияДлины1 ИЗ Справочник.Номенклатура
| ГДЕ Родитель <> Значение(Справочник.Номенклатура.ПустаяСсылка)
| ОБЪЕДИНИТЬ ВЫБРАТЬ Ссылка, Ссылка ИЗ Справочник.Номенклатура;";
Рефрен = "ВЫБРАТЬ РАЗЛИЧНЫЕ ПерваяДуга.НачалоДуги, ВтораяДуга.КонецДуги ПОМЕСТИТЬ ЗамыканияДлины#2 ИЗ ЗамыканияДлины#1 КАК ПерваяДуга
| ВНУТРЕННЕЕ СОЕДИНЕНИЕ ЗамыканияДлины#1 КАК ВтораяДуга ПО ПерваяДуга.КонецДуги = ВтораяДуга.НачалоДуги;
| УНИЧТОЖИТЬ ЗамыканияДлины#1;";
Эпилог = "ВЫБРАТЬ НачалоДуги Предок, КонецДуги Потомок ИЗ ЗамыканияДлины#2 ГДЕ НачалоДуги <> КонецДуги";
Запрос = Новый Запрос(СтрЗаменить(Пролог, "Номенклатура", ИмяСправочника));
МаксимальнаяДлинаЗамыканий = 1;
Пока МаксимальнаяДлинаЗамыканий < МаксимальнаяДлинаПути Цикл
Запрос.Текст = Запрос.Текст + СтрЗаменить(СтрЗаменить(Рефрен, "#1", Формат(МаксимальнаяДлинаЗамыканий, "ЧГ=0")), "#2", Формат(2 * МаксимальнаяДлинаЗамыканий, "ЧГ=0"));
МаксимальнаяДлинаЗамыканий = 2 * МаксимальнаяДлинаЗамыканий
КонецЦикла;
Запрос.Текст = Запрос.Текст + СтрЗаменить(Эпилог, "#2", Формат(МаксимальнаяДлинаЗамыканий, "ЧГ=0"));
Возврат Запрос.Выполнить().Выгрузить()
КонецФункции
В теле функции сначала собирается текст запроса. Он состоит из «пролога», который извлекает из базы данных исходное отношение, дополняет его путями нулевой длины и помещает результат во временную таблицу путей длины 1 и 0. Это единственная часть функции, которая зависит от структуры данных и типа исходного отношения. Далее следует «рефрен» - повторяемая часть запроса, в которой короткие пути соединяются в более длинные пути для новой временной таблицы, а также удаляется временная таблица, полученная на предыдущем шаге. Завершает текст запроса «эпилог», в котором извлекается итоговая временная таблица. После сборки полученный пакетный запрос единожды выполняется.
На первый взгляд может показаться, что текст запроса будет очень длинным. На самом деле, даже если справочник содержит миллион элементов в цепочке подчинения (мегаматрешка!), понадобится всего двадцать рефренов. Запрос будет в десятки (сотни?) раз короче некоторых запросов в ЗиУП.
Второе замечание, которое можно предупредить, это то, что, возможно, потребуется отдельный запрос для определения количества элементов в справочнике, чтобы оценить максимальную длину пути (уровень подчинения). Ответом здесь будет то, что на практике почти всегда можно будет взять некоторое достаточно большое число, например 256 или 1000, исходя из характера задачи.
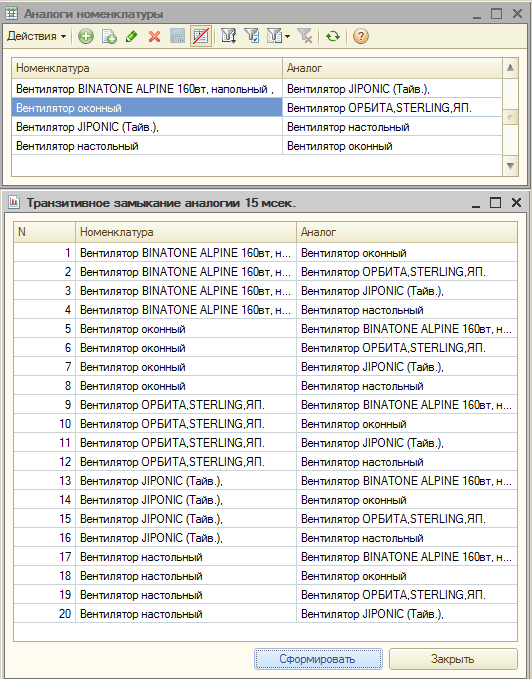
Третье замечание может заключаться в сомнениях: а насколько это будет быстро работать? Специально для скептиков прилагается отчет, работающий в любой конфигурации, который строит транзитивную иерархию любого справочника с замером времени выполнения запроса. Оно измеряется миллисекундами.
Ну и, наконец, для тех, кто заметил сходство математики предлагаемого метода и "Порождающего запроса" [//infostart.ru/public/90367/], могу добавить, что порождающий запрос появился именно вследствие данного решения.
P.S.: Если провести небольшой рефакторинг и перевести функцию на английский, она будет выглядеть компактней (всего 9 строк!)
function closure(name, N, M = 1) export
q = new query(strreplace("select parent a, ref b into r1 from catalog._ where parent <> value(catalog._.emptyref) union select ref, ref from catalog._;", "_", name));
while M < N do
q.text = q.text + strreplace(strreplace("select distinct p1.a, p2.b into r#2 from r#1 as p1 join r#1 as p2 on p1.b = p2.a; drop r#1;", "#1", format(M, "NG=0")), "#2", format(2 * M, "NG=0"));
M = 2 * M
enddo;
q.text = q.text + strreplace("select a Предок, b Потомок from r#2 where a <> b", "#2", format(M, "NG=0"));
return q.execute().unload()
endfunction
 (шутка). А вообще-то это не костыль, это (мой запрос) - трость! И даже весьма изящная.
(шутка). А вообще-то это не костыль, это (мой запрос) - трость! И даже весьма изящная.