1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Структура графа при использовании электромеханической аналогии определяется двумя таблицами: таблицей ребер и таблицей вершин.
Таблица ребер "Ребра" содержит три колонки: имя одной вершины ребра (Имя1), имя противоположной вершины ребра (Имя2) и значение упругости пружинки, которой моделируется ребро (Упругость).
| Имя1 | Имя2 | Упругость |
| Вершина1 | Вершина2 | Упругость1 |
| ... | ... | ... |
| ВершинаА | ВершинаБ | УпругостьАБ |
Значение упругости должно быть тем больше, чем теснее связаны вершины. Если граф представляет социальную сеть, то "упругость" может быть пропорциональна числу сообщений между соответствующими членами сети. Если граф представляет транспортную систему, то упругость будет тем меньше, чем больше расстояние между узлами.
Таблица вершин содержит две колонки: имя вершины (Имя) и значение электрического заряда вершины (Заряд).
| Имя | Заряд |
| Вершина1 | Заряд1 |
| ... | ... |
| ВершинаА | ЗарядА |
Величина заряда может быть пропорциональна месту, которое вершина должна занимать на рисунке, так как сильнее заряженная вершина будет с большей силой отталкивать соседние вершины. К примеру, при построении графа связей участников Инфостарта в качестве значения величины вершины (заряда) можно использовать рейтинг.
Текущее состояние системы определяется таблицей состояния, содержащей текущие координаты вершин и состоящей из колонок: имя вершины (Имя), текущая координата по горизонтали (Х) и координата по вертикали (У). Таблицу вершин и таблицу состояния для простоты можно объединить, записывая заряд и текущие координаты в одну таблицу "Вершины".
| Имя | Заряд | Х | У |
| Вершина1 | Заряд1 | Х1 | У1 |
| ... | ... | ... | ... |
| ВершинаА | ЗарядА | ХА | УА |
Динамику описанной системы можно смоделировать методом Эйлера. Он позволяет получить координаты вершин через небольшой промежуток времени на основе текущих координат, зная скорость и направление (вектор) перемещения каждой вершины.
Для наших целей проще предположить, что скорость перемещения пропорциональна силе, действующей на вершину (движение в вязкой среде). Чтобы найти силу, действующую на конкретную вершину, нужно сложить все силы, действующие на нее со стороны других вершин. Сила действия со стороны каждой вершины будет состоять из силы отталкивания, определяемой законом Кулона в пропорции произведению зарядов вершин, деленному на квадрат расстояния между ними. И силы притягивания в случае наличия связи (ребра). Величина силы притягивания подчиняется закону Гука, то есть прямо пропорциональна произведению упругости связи на расстояние между вершинами. В итоге на вершину А с координатами А.Х и А.У со стороны вершины Б с координатами Б.Х и Б.У по горизонтали будет действовать сила отталкивания
(А.Х – Б.Х) / РасстояниеАБ * А.Заряд * Б.Заряд / ((А.Х – Б.Х) * (А.Х – Б.Х) + (А.У – Б.У) * (А.У – Б.У))
а по вертикали сила отталкивания
(А.У – Б.У) / РасстояниеАБ * А.Заряд * Б.Заряд / ((А.Х – Б.Х) * (А.Х – Б.Х) + (А.У – Б.У) * (А.У – Б.У))
где
РасстояниеАБ = SQRT((А.Х – Б.Х) * (А.Х – Б.Х) + (А.У – Б.У) * (А.У – Б.У))
Элементы вида (А.Х – Б.Х) / РасстояниеАБ - это проекции вектора направления силы, имеющего единичную длину. Такой вектор влияет на направление, но не меняет величину силы.
При наличии ребра между вершинами также будет действовать сила притягивания. По горизонтали ее величина будет определяться формулой
((Б.Х – А.Х) / РасстояниеАБ) * УпругостьАБ * РасстояниеАБ,
А по вертикали формулой
((Б.У – А.У) / РасстояниеАБ) * УпругостьАБ * РасстояниеАБ.
Сложив две силы и произведя необходимые сокращения, получим формулу горизонтальной силы
(А.Х – Б.Х)(А.Заряд * Б.Заряд / РасстояниеАБ / ((А.Х – Б.Х) * (А.Х – Б.Х) + (А.У – Б.У) * (А.У – Б.У)) – УпругостьАБ)
и вертикальной силы
(А.У – Б.У)(А.Заряд * Б.Заряд / РасстояниеАБ / ((А.Х – Б.Х) * (А.Х – Б.Х) + (А.У – Б.У) * (А.У – Б.У)) – УпругостьАБ)
Перемещение по Х и У можно получить, умножив сумму сил, действующих со стороны всех вершин, на величину шага по времени «Шаг». Таким образом, если известны текущие координаты вершин, применив указанные формулы, можно получить следующие координаты и так далее, пока система не перейдет в устойчивое состояние, где величина суммы сил, действующих на каждую вершину, будет близка к нулю.
Все вышесказанное реализуется повторением выполнения одного достаточно простого запроса:
ВЫБРАТЬ Ребра.Имя1, Ребра.Имя2, Ребра.Упругость
ПОМЕСТИТЬ Ребра ИЗ &Ребра КАК Ребра
;
ВЫБРАТЬ Ребра.Имя1, Ребра.Имя2, Ребра.Упругость
ПОМЕСТИТЬ Дуги
ИЗ Ребра КАК Ребра
ОБЪЕДИНИТЬ ВСЕ
ВЫБРАТЬ Ребра.Имя2, Ребра.Имя1, Ребра.Упругость
ИЗ Ребра КАК Ребра
ИНДЕКСИРОВАТЬ ПО Ребра.Имя1, Ребра.Имя2
;
ВЫБРАТЬ Вершины.Имя, Вершины.Заряд, Вершины.Х, Вершины.У
ПОМЕСТИТЬ Вершины
ИЗ &Вершины КАК Вершины
;
ВЫБРАТЬ
А.Имя,
МАКСИМУМ(А.Заряд) КАК Заряд,
МАКСИМУМ(А.Х) + &Шаг * СУММА((А.Х - Б.Х) * (А.Заряд * Б.Заряд / ((А.Х - Б.Х) * (А.Х - Б.Х) + (А.У - Б.У) * (А.У - Б.У)) - ЕСТЬNULL(Дуги.Упругость, 0))) КАК Х,
МАКСИМУМ(А.У) + &Шаг * СУММА((А.У - Б.У) * (А.Заряд * Б.Заряд / ((А.Х - Б.Х) * (А.Х - Б.Х) + (А.У - Б.У) * (А.У - Б.У)) - ЕСТЬNULL(Дуги.Упругость, 0))) КАК У
ИЗ
Вершины КАК А
ВНУТРЕННЕЕ СОЕДИНЕНИЕ Вершины КАК Б
ПО А.Имя <> Б.Имя
ЛЕВОЕ СОЕДИНЕНИЕ Дуги КАК Дуги
ПО А.Имя = Дуги.Имя1
И (Б.Имя = Дуги.Имя2)
СГРУППИРОВАТЬ ПО
А.Имя
В первом запросе пакета вводится таблица ребер, во втором из ребер формируются дуги, то есть учитывается то, что силы ребра направлены как от первой ко второй вершине, так и от второй к первой, в третьем запросе вводится таблица вершин, а в четвертом выполняются необходимые вычисления. Для этого соединяются три таблицы: таблица вершин А и таблица вершин Б по условию неравенства имен вершин и таблица дуг по условию совпадения имен концов дуг с именами вершин. Далее производится группировка по вершинам таблицы А, в процессе которой рассчитывается суперпозиция сил, которая умножается на Шаг и складывается с текущими координатами.
Внимательные читатели заметят, что в формулах пропущен делитель «РасстояниеАБ». Это сделано из-за того, что в языке запросов 1С нет функции расчета квадратного корня SQRT. То есть в данном запросе фактически считается, что сила отталкивания обратно пропорциональна не квадрату расстояния между вершинами, а просто расстоянию. Таким образом, силе отталкивания придается избыточное дальнодействие. Ничего страшного в этом нет, так как для задачи рисования графов это не столь существенно. Однако в запросе, реально используемом в обработке, эта трудность преодолена. Это сделано за счет расчета квадратного корня по итерационной формуле Герона
РасстояниеАБ’ = (РасстояниеАБ + КвадратРасстоянияАБ / РасстоянияАБ) / 2,
где предыдущее значение расстояния берется из предшествующей итерации запроса, а начальное равно единице. Такое решение совсем не на много замедлило процесс вычислений. Указанный режим включается в обработке галочкой «ЗаконКулона». Также в реальном запросе проведена дополнительная оптимизация: исключена повторная загрузка дуг и индексация дуг в каждой итерации, а сумма квадратов расстояний для каждой пары вершин считается не четыре раза, как в исходном запросе, а один. При желании, чтобы исключить квадратичную зависимость времени выполнения запроса от числа вершин, можно разбивать плоскость на клетки (или соты) и считать отталкивание только для вершин соседних клеток. Однако пока такой оптимизации не проводилось и непонятно, насколько это необходимо – для рисования графов из 100 – 200 вершин быстродействия достаточно.
Как и в других задачах численного решения систем нелинейных дифференциальных уравнений важным является вопрос выбора шага по времени. БОльшая величина шага приводит к увеличению скорости решения, но до определенных пределов, когда динамическая система теряет устойчивость. Во всех следующих примерах при зарядах и упругости 1 шаг брался равным 0,2, кроме графов групп номенклатуры и контрагентов, где шаг пришлось уменьшить до 0,05. В целом действует понятное правило – чем больше упругость, тем меньше шаг.
2. ПРАКТИЧЕСКАЯ ЧАСТЬ
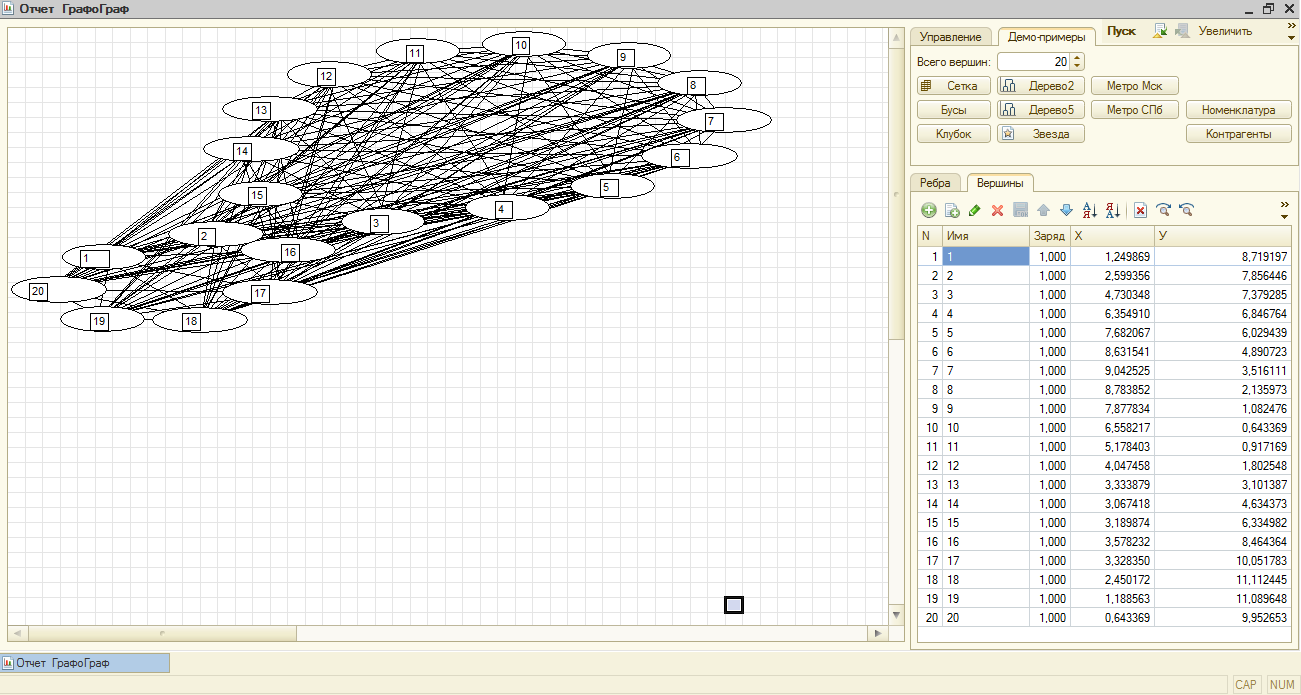
К статье приложена обработка «ГрафОграф» (ударение на букве «о»). С ее помощью можно задать структуру графа и пронаблюдать динамику построения его рисунка (если включен флажок «Показывать процесс»). Обработка позволяет менять шаг решения - он должен быть положительным, но не слишком большим. Можно менять порог перемещения для остановки – этот параметр может быть равен нулю, но тогда придется прерывать процесс моделирования вручную (Ctrl-Break). Можно задавать требуемый размер графа в миллиметрах – граф автоматически масштабируется, стараясь занять заданный прямоугольник. Можно увеличивать или уменьшать граф, а также (на вкладке вершины), поворачивать его по часовой стрелке или против часовой стрелки или зеркально отображать (относительно диагонали). Можно задавать цвет ребер и цвет вершин (всех одновременно – различный цвет для каждой вершины и ребра задавать пока не было необходимости). Кроме того, задав первому ребру упругость, с помощью кнопки «Сравнять», можно сделать упругость всех ребер такой же, как у первого ребра. Аналогичное действие запрограммировано для заряда вершин. Вот как выглядит панель управление обработкой:
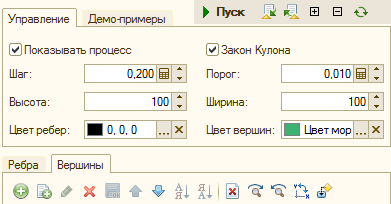
Структуру графа можно задать вручную, задав его список ребер. Соединяемые вершины определяются именами, представленными текстовыми строками. В конкретном применении обработку можно специализировать так, чтобы вершины задавались ссылками на объекты информационной базы. Тогда расшифровка позволит открывать соответствующие объекты. Список вершин при редактировании ребер формируется автоматически (заряд можно поправить). Набранные параметры и структуру графа можно сохранить как настройки отчета.
Если нет графа, рисунок которого хочется посмотреть, можно поработать с готовыми демо-примерами. При этом можно выбрать число вершин графа-примера (по умолчанию 64).
Далее приведены рисунки, полученные для зашитых в обработку примеров. Динамику построения (а она также весьма интересна) лучше посмотреть, запустив обработку.
1. Сетка (соседние вершины соединены в ячейки прямоугольной сетки)
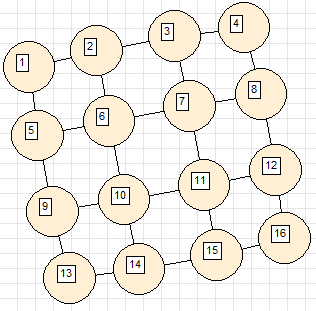
2. Ожерелье (вершины связаны в кольцо)
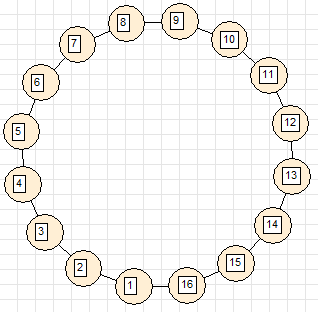
3. Клубок (все вершины непосредственно связаны)
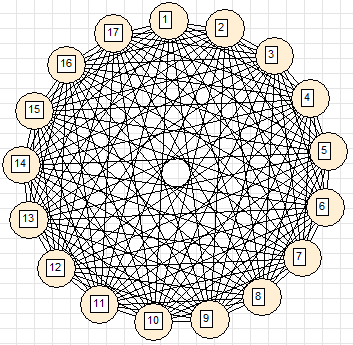
чтобы получить эту красивую картинку, потребовалось обнулить упругости ребер в середине кольца. Иначе вид был бы совсем другим:
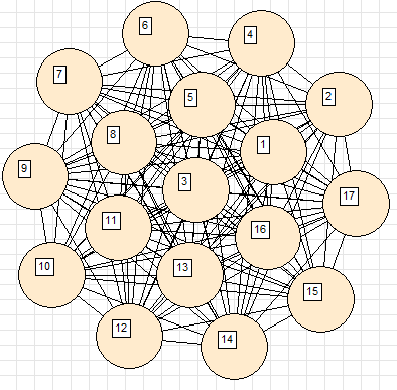
4. Бинарное дерево
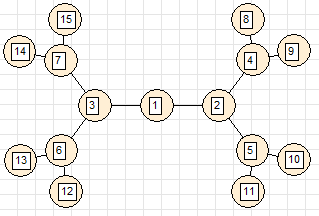
5. 5-арное дерево
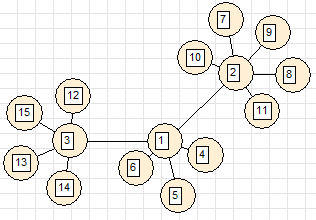
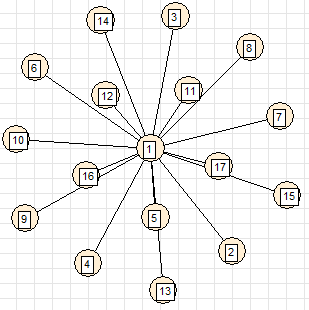
6. Звезда (все вершины соединены с одной центральной вершиной)
здесь хорошо виден врожденный недостаток метода - прямое ребро 1-13 не обходит вершину 5, а пересекает ее.
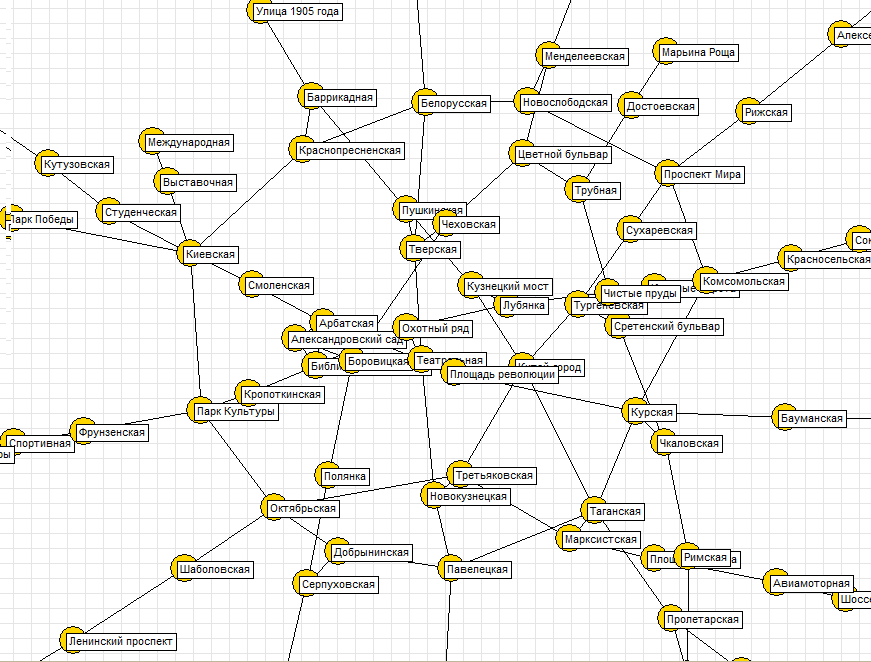
7. Метро Москва
при увеличении рисунка схема хорошо читается. В доказательство приведен фрагмент центральной части при бОльшем увеличении
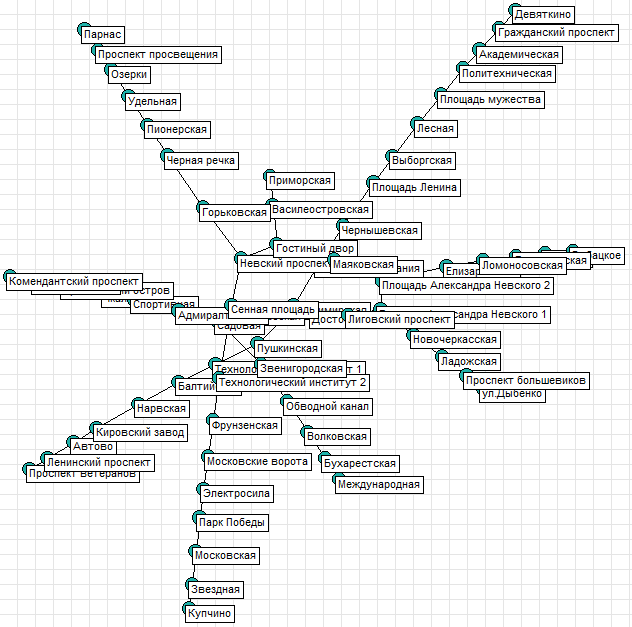
8. Метро Питер
Тот, кто знает Питер, обратит внимание, что станции Василеостровская и Приморская не на своем месте, но тут уж ничего не поделаешь - такая модель.
9. Граф счетов бухгалтерского учета
(этот пример перенесен в следующую статью)
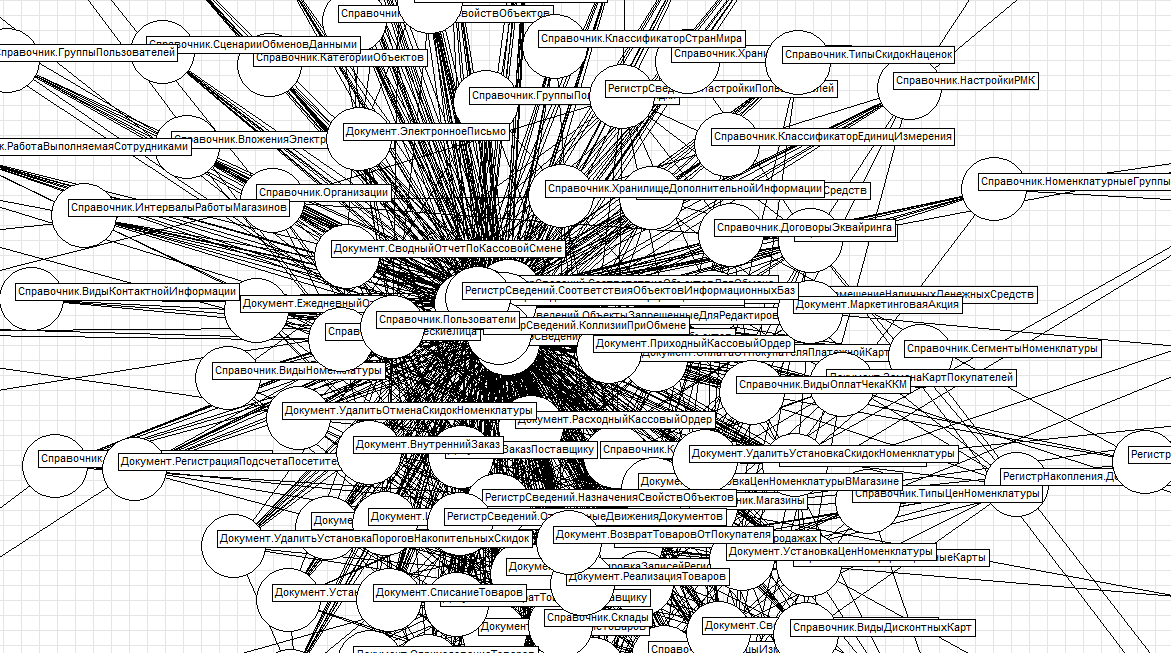
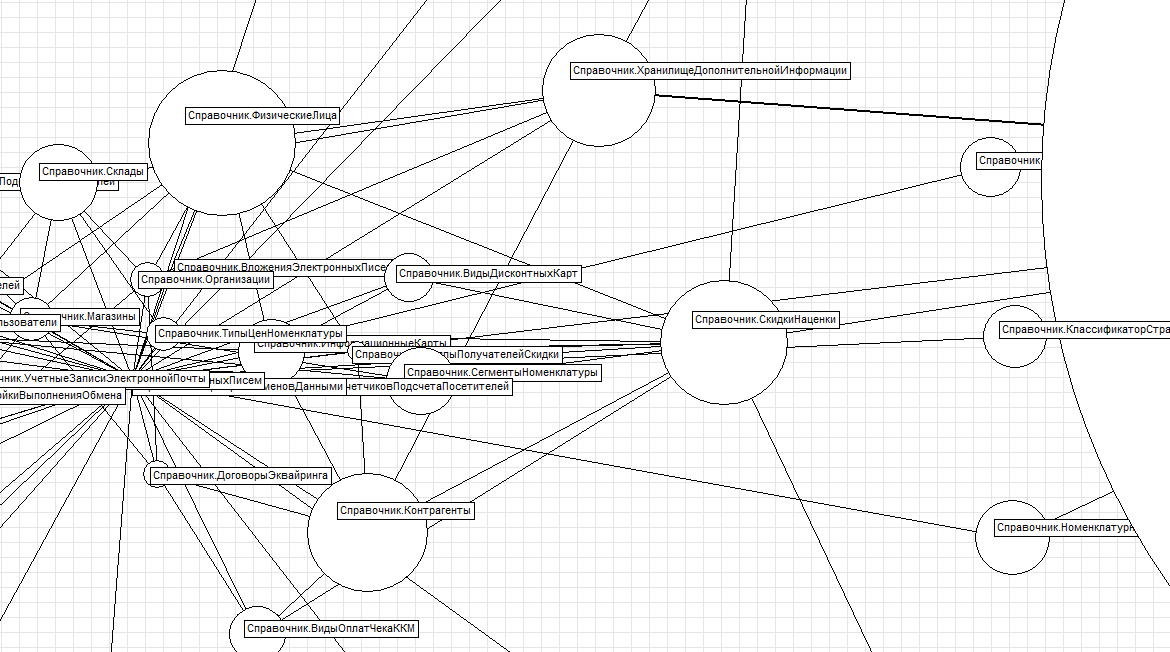
10. Граф групп справочника «Номенклатура» (такой справочник должен существовать в конфигурации, где запускается обработка)
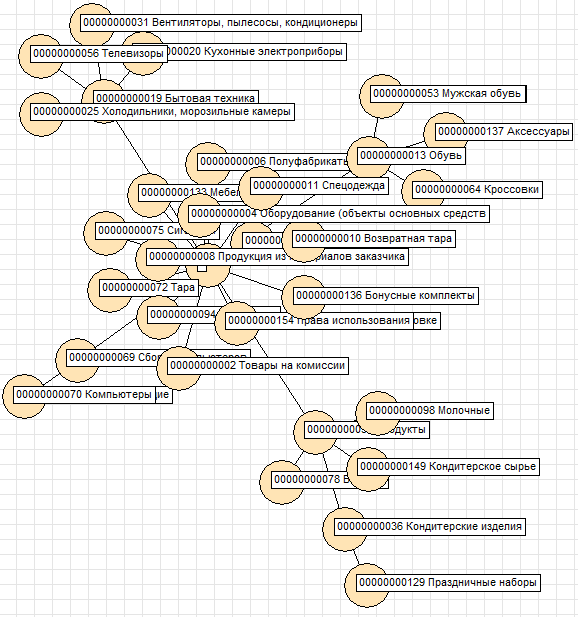
11. Граф групп справочника «Контрагенты» (этот справочник также должен существовать в конфигурации, где запускается обработка)
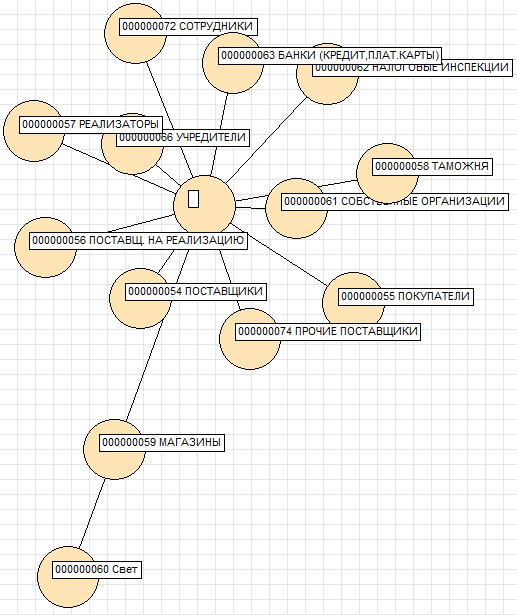
По поводу схем метро можно добавить, что при их построении пришлось пойти на определенную хитрость. Дело в том, что из-за начального случайного расположения станций длинные радиальные ветки за кольцевой линией (для Москвы) с большой вероятностью перехлестываются и далее уже не выправляются. Можно было бы (а) строить граф наращиванием станций (как строилось метро), (б) соединять средние станции вылетных веток большим виртуальным кольцом со слабыми «выправляющими» связями, (в) закреплять конечные станции или (г) при начальном рассеивании станций учесть округ станции. Был выбран последний метод. Также стоит отметить, что число (187 с учетом одноименных) станций московского метро уже близко к пределу возможностей метода. В строке состояния при работе метода отмечается число кадров в секунду, которые успевает построить обработка. На примере метро обработка (файловая база, ноутбук, отключен показ процесса и закон Кулона) показывала примерно 2,4 fps. Структура метро записана в макетах обработки, при желании можно добавить изображение и любого другого метро.
Все остальные рисунки строятся практически мгновенно или достаточно быстро и полностью автоматически по информации только о структуре графов. Использовалось только масштабирование и поворот. Относительно небольшое число вершин, изображенных на примерах объясняется не ограниченными возможностями метода, а желанием сделать рисунки меньше.
Кажется, этих примеров должно быть достаточно для доказательства работоспособности и практической применимости метода. Но представление отношений в виде графов настолько универсально, что, без сомнения, найдется еще немало других показательных примеров. В частности, можно было еще построить какое-либо генеалогическое дерево, структуру комментариев к выбранной статье на Инфостарте, связи пользователей «1С: Документооборот» и так далее и тому подобное. Добавив несколько строк кода, можно изображать на дугах стрелки и, таким образом, рисовать ориентированные графы.
Можно предложить и другие способы «конфигурирования» данной «типовой» модели под конкретную задачу, кроме вершин-объектов, разноцветных вершин, разноцветных дуг и стрелок на них. Например, крайне легко добавляется третье измерение и решается задача размещения вершин в пространстве. Можно закреплять некоторые вершины, каждый раз обнуляя рассчитанное перемещение. После этого можно добавить «течение», чтобы вершины «относило» в нужную сторону. Ну, или ввести силу отталкивания вершин и от дуг тоже, чтобы скорректировать врожденный недостаток рассмотренного алгоритма – пересечение дугами «чужих» вершин.
ВЫВОДЫ
В итоге по результатам тестирования обработки на перечисленных примерах можно сделать такие выводы: метод идеально работает в случае относительно неплотных графов симметричной и регулярной структуры. В случае другой крайности - сложной запутанной структуры графа иногда (но не всегда!) может потребоваться ручная коррекция некоторых параметров (шаг, заряд, закон отталкивания, упругость, текущие координаты) или даже выбор принципиально другого алгоритма. Есть ограничения (в теории - преодолимые) и по размеру графа. Но, с другой стороны, в отличие от других алгоритмов, реализация данного метода выполнима на чистом 1С без использования каких-либо внешних компонент простым запросом из 14-ти строк (в основной части).
Ну а в целом рассмотренный подход еще раз показывает гибкость языка запросов и то, насколько взаимосвязаны научные дисциплины. При решении данной конкретной практической задачи автоматизации потребовались знания из нескольких различных областей математики и физики. Пригодилась даже теорема Пифагора. В общем, знания – сила!
Вступайте в нашу телеграмм-группу Инфостарт