Вводная часть
В настоящий момент можно выделить два основных концептуальных (на уровне основных идей, понятий) подхода к использованию Графов затрат в учетных системах. Первый подход предполагает «жесткое» встраивание Графа затрат в учетную систему, когда разработчики настраивают правила формирования узлов и дуг Графа затрат с одной единственной целью – произвести расчет фактической себестоимости в конце периода. Предполагается, что это первый … и последний этап расчета себестоимости, решения каких-либо других задач на Графах затрат данный подход не предусматривает. Можно сказать, что на данный момент этот концептуальный подход является доминирующим и используется разработчиками в подавляющем числе учетных систем.
По большому счету в этом случае пользователю достаточно минимальных знаний о теории Графов затрат, а часто достаточно просто знать о самом факте существования такой математической модели. Получить дополнительную аналитическую информацию о структуре себестоимости в этом случае можно только извлекая ее из уже полученных результатов расчета себестоимости с помощью различных алгоритмов агрегирования данных (отчетов) и/или проводя дополнительные внесистемные расчеты.
Однако, возможен и другой концептуальный подход к использованию Графов затрат, рассматривающий процедуру закрытия затрат периода как необходимый, но все-таки только начальный этап исследования структуры себестоимости. На этом начальном этапе формируется математическая модель – Граф затрат, который можно взять за основу и далее решать с его помощью различные задачи анализа себестоимости, получая аналитическую информацию, подчас недоступную на единственном этапе закрытия затрат периода.
Используя профессиональный сленг учетных специалистов можно сказать, что данный подход исходит из возможности делать не одно (первое … и последнее), а сколько угодно «закрытий» затрат периода, каждый раз корректируя исходный (далее – базовый) Граф затрат и получая в результате дополнительную аналитическую информацию о структуре себестоимости.
Используя научную терминологию, в данном случае можно говорить о возможности проведения целого ряда численных экспериментов с целью исследования структуры себестоимости на математической модели в виде Графа затрат. Напомним, что эксперимент (в том числе и численный) является одним из методов научного познания. Далее в статье мы рассмотрим два таких численных эксперимента:
- сначала рассчитаем фактическую себестоимость методом direct-costing (проведем «обычное» закрытие затрат периода)
- используя базовый Граф затрат, сформированный для предыдущего численного эксперимента, рассчитаем с его помощью фактическую себестоимость методом absorption-costing (найдем полную себестоимость)
Ограничимся этим набором численных экспериментов, поскольку для целей статьи важно не их количество (принципиальных ограничений на число экспериментов нет), а понимание принципа использования Графа затрат в данном концептуальном подходе. Тем более, что на сайте infostart.ru есть достаточное число статей, в которых рассматриваются как элементы теории Графов затрат, так и решения различных практических задач на Графах затрат.
Расчет фактической себестоимости методом директ-костинг
Рассмотрим пример расчета себестоимости для экономического субъекта, в организационной структуре которого выделены три отдела, три цеха и офис (административный персонал). Отделы выполняют работы (измеряемые в часах) для других отделов, цехов и офиса. Цех1 произвел за период 12 изделий (Изд1), 10 из которых были проданы. Цех2 произвел 10 изделий (Изд2), все были проданы. Цех 3 произвел 26 изделий (Изд3), 22 из которых были использованы в производстве Цехом1 и Цехом2.
Стоимость управленческих услуг Офиса полностью включается в расходы отчетного периода (метод direct-costing). Поскольку в настоящий момент для целей бухгалтерского учета этот метод расчета себестоимости является безальтернативным (см. ФСБУ5 «Запасы»), то расчет себестоимости в данном случае можно считать «обычной» процедурой закрытия затрат периода.
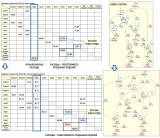
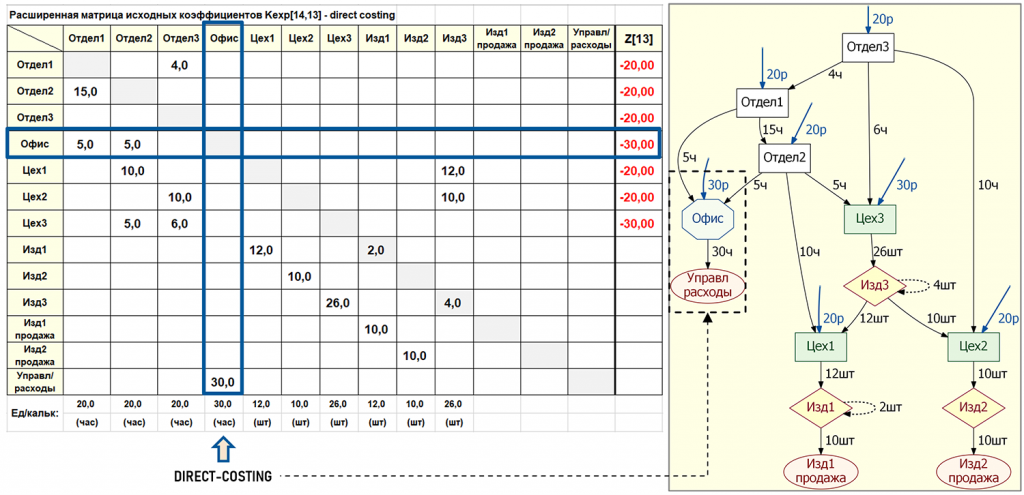
Ниже на рисунке представлена расширенная матрица исходных коэффициентов для данной задачи (формируется на основании бухгалтерских записей экономического субъекта за период).
Наиболее удобной для решения задач на Графах затрат является (по мнению автора) матричная форма Графа затрат. Основной матрицей, от корректного формирования которой зависят все остальные этапы решения задачи, является расширенная матрица исходных коэффициентов, содержащая в себе все необходимые данные для расчета себестоимости с помощью СЛАУ.
Напомним, что прямоугольная расширенная матрица исходных коэффициентов состоит из квадратной матрицы исходных коэффициентов и присоединенного справа вектора-столбца правых частей уравнений. Источники затрат расположены в столбцах матрицы исходных коэффициентов, получатели затрат в ее строках (это аналог бухгалтерской «шахматки»).
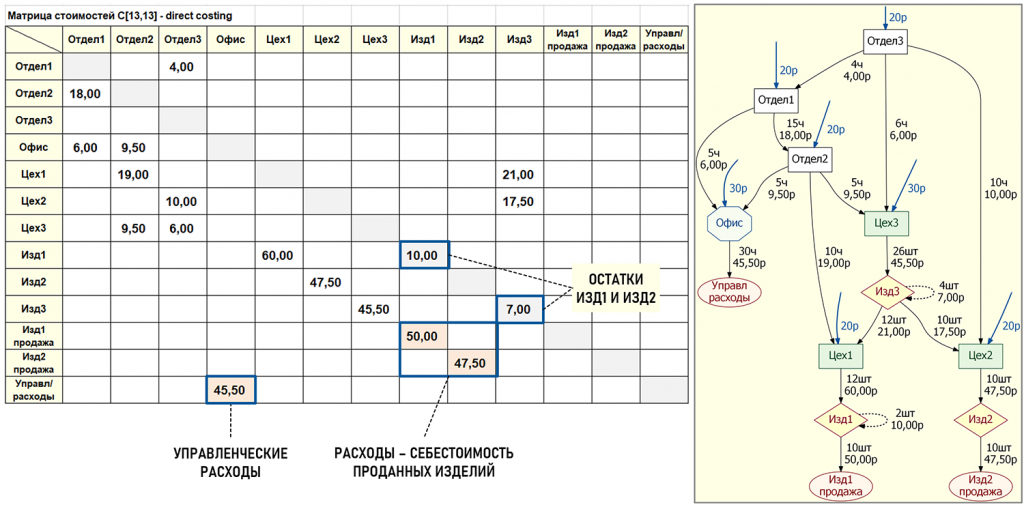
Остатки (количество) изделий на конец периода показаны на главной диагонали матрицы исходных коэффициентов, а также пунктирными дугами, которые начинаются и заканчиваются на одних и тех же центрах затрат Изд1 и Изд3. Эту ситуацию также можно отобразить пунктирными дугами, «просто» исходящими из центров затрат Изд1 и Изд3, пользователь может выбрать, какой вариант ему удобнее.
Также на рисунке хорошо видно, как идея расчета себестоимости методом директ-костинг воплощается в математической модели – в Офис поступают первичные затраты (30р) и вторичные затраты от Отдела1 (5ч) и Отдела2 (5ч), а исходящие вторичные затраты Офиса (30ч) полностью попадают только в финишный центр затрат УправлРасходы (аналог счета 90.08 «Управленческие расходы»). В нашем примере управленческие услуги административного персонала измеряются в часах. Себестоимость проданных изделий формируется в центрах затрат Изд1Продажа и Изд2Продажа (аналоги счета 90.02 «Себестоимость продаж»).
Если удалось сформировать расширенную матрицу исходных коэффициентов, то задачу расчета себестоимости фактически можно считать решенной. Творческая часть задачи на этом заканчивается так как далее следует выполнить чисто технические процедуры – выбрать численный метод решения СЛАУ и, собственно, выполнить саму процедуру решения. Поэтому, когда мы будем далее говорить о работе с моделью в виде Графа затрат для проведения численных экспериментов, то в первую очередь это будет означать работу именно с расширенной матрицей исходных коэффициентов.
Результаты процедуры закрытия затрат периода (решения СЛАУ) представлены ниже на рисунке.
Мы не будем заниматься анализом полученных результатов, поскольку это обычная процедура расчета себестоимости и все результаты наглядно представлены на рисунке. В контексте темы данной статьи в первую очередь нас интересует сформированная математическая модель – базовый Граф затрат, для целей статьи это можно считать основным результатом данного (начального) этапа расчета себестоимости.
Опираясь на эту базовую модель и внося в нее корректировки, далее можно решать различные учетные задачи. Например, дальше будет показано как можно использовать эту базовую модель для проведения численного эксперимента, целью которого является исследование структуры полной себестоимости проданных изделий.
Расчет фактической полной себестоимости
В настоящее время доминирует мнение, что в учетной системе можно реализовать расчет себестоимости только каким-либо одним методом, например, методом direct-costing ИЛИ методом absorption-costing (расчет полной себестоимости). Считается, что расчет себестоимости за период одновременно двумя (или более) методами является слишком сложной задачей. Посмотрим, так ли это на самом деле?
Проведем численный эксперимент целью которого будет исследование полной себестоимости проданных изделий – причем сделаем это для того же экономического субъекта и отчетного периода, для которого выше была рассчитана себестоимость методом директ-костинг. Также важно отметить, что опираться при этом будем на те же первичные учетные данные, что и в первом численном эксперименте.
Далее мы увидим, что для решения этой задачи нет необходимости перестраивать всю учетную систему под цели определения полной себестоимости. Достаточно будет просто немного модифицировать базовый Граф затрат, чтобы с помощью практически тех же самых первичных учетных данных рассчитать полную себестоимость проданных изделий. Это важное исследование, поскольку расчет полной себестоимости необходим в том числе для определения цены продаваемых изделий.
В базовом Графе затрат все входящие первичные и вторичные затраты Офиса в полном объеме включаются в расходы периода, то есть передаются в центр затрат УправлРасходы. Для расчета полной себестоимости проданных изделий нужно чтобы Офис распределил свои исходящие вторичные затраты между всеми отделами и цехами. В примере для простоты это распределение будет происходить в равных долях.
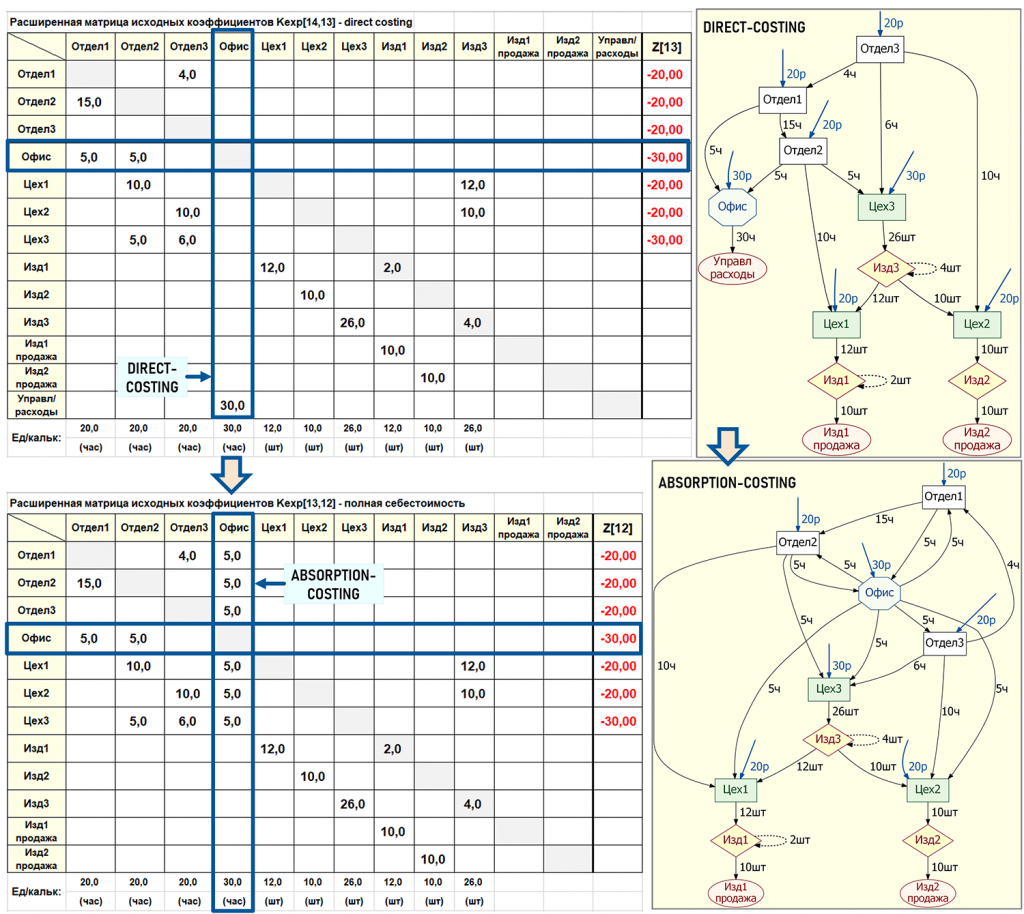
Ниже на рисунке показано каким образом преобразуется в этом случае расширенная матрица исходных коэффициентов базового Графа затрат. Для сравнения на рисунке показаны обе расширенные матрицы исходных коэффициентов – для расчета методом директ-костинг и для расчета полной себестоимости.
Как видим, для решения задачи потребовались совсем незначительные корректировки базовой модели. Во-первых, изменились значения элементов в столбце Офис, теперь управленческие затраты в равных долях передаются всем отделам и цехам. Во-вторых, уменьшилась размерность расширенной матрицы исходных коэффициентов, поскольку из базовой модели за ненадобностью были удалены строка и столбец для центра затрат УправлРасходы, на который «стекались» управленческие затраты при расчете себестоимости методом директ-костинг.
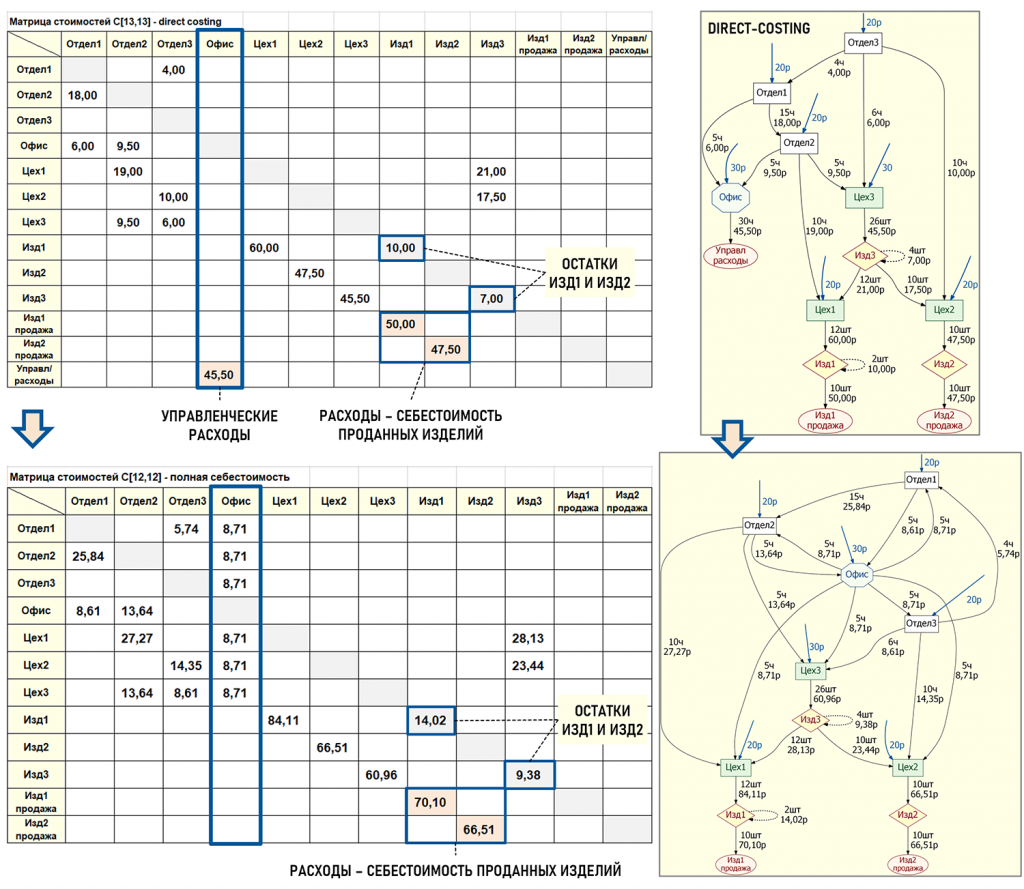
Вот, собственно, и все корректировки базового Графа затрат. Все остальные значения элементов расширенной матрицы исходных коэффициентов остались неизменными. Теперь можно произвести расчет полной себестоимости проданных изделий (решить СЛАУ). Ниже на рисунке представлены результаты расчета (с учетом погрешностей округления), причем для сравнения на рисунке показаны две матрицы стоимостей – для расчета методом директ-костинг и для расчета полной себестоимости.
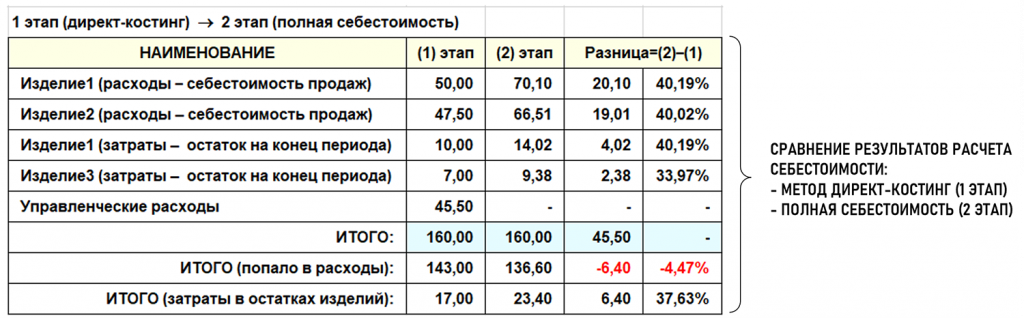
Проведем анализ полученных результатов. Ниже на рисунке в таблице показано как меняются значения себестоимости проданных изделий (расходов) и остатков готовых изделий на конец периода при переходе от расчета методом директ-костинг к расчету полной себестоимости.
В таблице видно, что при расчете полной себестоимости общие расходы экономического субъекта уменьшились на 6,40р (-4,47%) со 143р до 136,60р. Это произошло потому, что часть управленческих расходов попала (увеличила) не только в себестоимость проданных изделий, но и увеличила стоимость остатков готовых изделий – на 4,02р (40,19%) увеличилась стоимость остатка Изд1 и на 2,38р (33,97%) увеличилась стоимость остатка Изд3.
Это важный нюанс, поскольку часто для определения полной себестоимости проданной продукции используется упрощенный внесистемный расчет, при котором вся сумма управленческих расходов «просто» распределяется между себестоимостями проданных видов продукции. При этом стоимость остатков готовой продукции и затрат в незавершенном производстве на конец периода остаются неизменными, что приводит к завышению себестоимости проданной продукции рассматриваемого периода и занижению этой себестоимости в следующих периодах.
Выводы
Как было сказано в начале статьи, сейчас можно выделить два основных концептуальных подхода к использованию Графов затрат в учетных системах.
В первом подходе основной целью разработчиков является «жесткое» встраивание Графа затрат в учетную систему для решения всего одной задачи – расчета фактической себестоимости в конце периода, решения каких-либо других задач на Графах затрат данный подход не предусматривает.
Второй подход предполагает многократное использование Графа затрат для решения интересных пользователю учетных задач. Например, как это было сделано в статье.
Оба подхода имеют право на существование. Если хозяйственная жизнь экономического субъекта более-менее «стабильна», то есть все его хозяйственные и учетные процессы выстроены и практически не меняются от периода к периоду, то в этом случае вполне достаточно первого подхода к использованию Графов затрат. Тем более, что для этого учетным специалистам нет необходимости как-то глубоко изучать теорию Графов затрат, достаточно минимальных знаний по этой теме. Кстати сказать, этот подход к использованию Графов затрат сейчас доминирует.
Если же хозяйственная жизнь экономического субъекта достаточно «волатильна», то есть его хозяйственные и учетные процессы могут меняться от периода к периоду, то в этом случае предпочтительнее второй подход к использованию Графов затрат. При «волатильной» хозяйственной жизни приходится решать много учетных задач, связанных, например, с выбором того или иного сценария хозяйственной деятельности и/или с оценкой фактических результатов хозяйственной деятельности с разных позиций.
Тем более, что при работе с Графами затрат не имеет никакого значения о какой себестоимости идет речь – о фактической, плановой, прогнозной или какой-то другой. В статье мы рассматривали расчет фактической себестоимости, но с таким же успехом могли заменить прилагательное фактическая на плановая и говорить о плановой себестоимости. «Математика» расчета от этого никак не меняется, в конечно итоге экономическим смыслом результаты расчета всегда наделяет пользователь.
В заключение необходимо отметить, что при втором подходе к использованию Графов затрат в архитектуре учетной системы желательно предусмотреть отдельный модуль для работы с Графами затрат. Связь между этим модулем и «основной» бухгалтерской базой данных может осуществляться в форме «подключенной» системы.
Это означает, что модуль должен иметь свое хранилище данных, отделенное от хранилища данных бухгалтерии, первичные учетные данные могут импортироваться в модуль из «основной» бухгалтерской базы данных и снабжаться дополнительными свойствами, а результаты расчета себестоимости могут экспортироваться обратно, например, в виде бухгалтерских проводок документа Закрытие затрат периода. Также в модуле должна быть математическая библиотека с набором «быстрых» численных методов решения СЛАУ, интерактивной подсистемой визуализации потоков затрат и т.д., но это уже отдельная тема для обсуждения.
Вступайте в нашу телеграмм-группу Инфостарт