Об игре
Пентамино - фигура, состоящая из пяти квадратов, соединенных сторонами. Является частным случаем полимино. Другие разновидности полимино - тетрамино и гексамино, из, соответственно, четырех и шести квадратов. В процессе игры необходимо набор фигур "уложить" в прямоугольник заданного размера. Сделать это, зачастую, весьма непросто!
Управление:
1. с помощью мыши:
- "захват" и "освобождение" фигуры - клик мышью в клетку фигуры
- перемещение - клик в другую клетку поля
- поворот и отражение фигуры - кнопки командной панели
2. с помощью клавиатуры:
- "захват" и "освобождение" фигуры - <enter> в выделенной ячейке - клетке фигуры
- перемещение - <стрелки клавиатуры>
- поворот фигуры - клавиши <A> и <Z>
- отражение фигуры - клавиши <S> и <X>
Всего может быть 12 различных фигур пентамино. Из них можно сложить прямоугольники (площадью 60 квадратов): 6×10, 5×12, 4×15 и 3×20. Из полного набора гексамино (35 возможных фигур) или тетрамино (5 фигур) сложить какой-либо прямоугольник нельзя, но это можно сделать, взяв неполный набор, или добавив к набору дополнительные фигуры. Разумеется, прямоугольники можно складывать из произвольного набора фигур, в том числе повторяющихся. В игре реализованы классические головоломки пентамино 6×10, 5×12, 4×15 и 3×20, тетрамино 4×6, а также, самый интересный, пользовательский вариант.
В пользовательском режиме можно выбрать: вид фигуры (тетрамино, пентамино или гексамино), размер поля-прямоугольника (а значит, и количество фигур) и сложность. Сложность определяет возможность использовать повороты и отражения фигур. Набор фигур генерируется случайным образом.
Генерация фигур
Вот как раз генерация набора фигур - самая интересная и сложная задача. В чем сложность? А в том, что у головоломки обязательно должно быть решение, т.е. все фигуры гарантированно должны поместиться в прямоугольник. Как этого добиться? Ну, во-первых, можно попытаться математически доказать разрешимость головоломки при заданном наборе фигур. Я не знаю как это сделать:), кто захочет - может попробовать. Во-вторых можно написать алгоритм, "решающий" эту задачу, это тоже весьма интересно. Но я пошел по третьему пути - от обратного, т.е. не составлять прямоугольник, а наоборот, случайным образом разбить исходный прямоугольник на составные части заданного размера. Расскажу поподробнее.
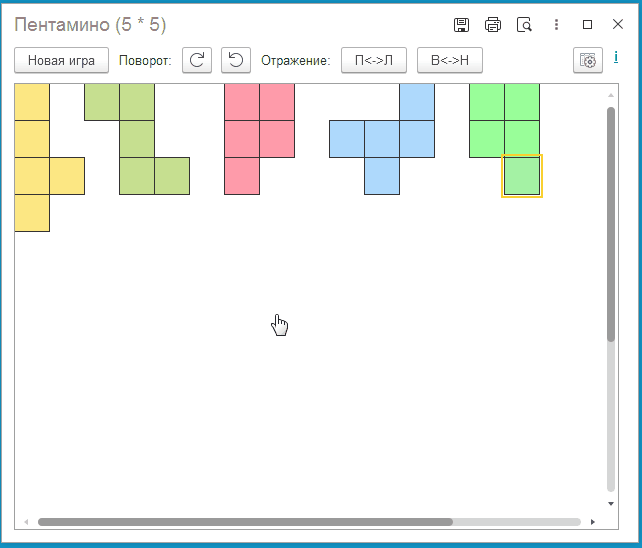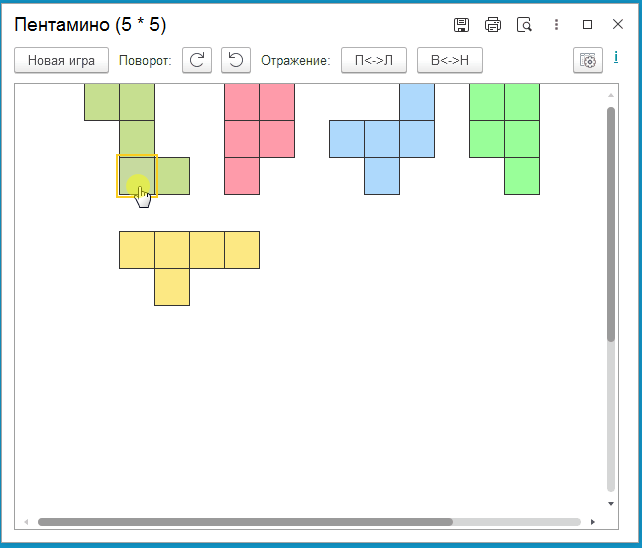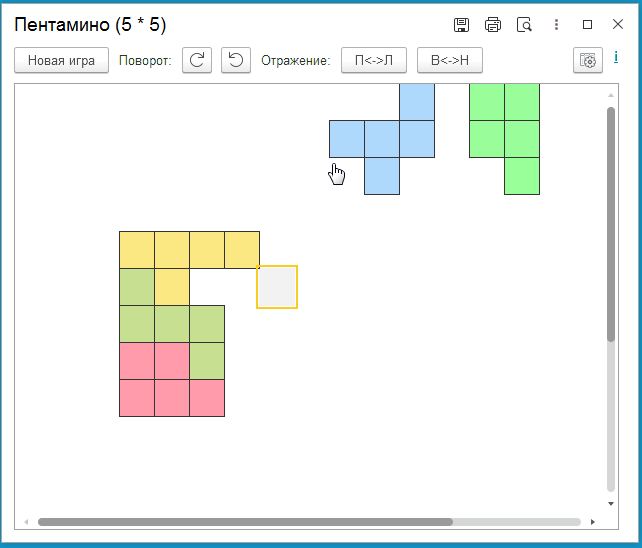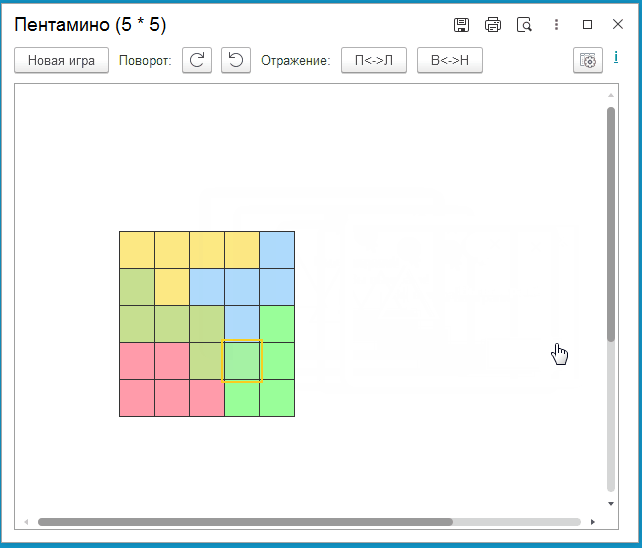
1. Генерация начинается со случайной расстановки "затравок" - по одной клетке от каждой фигуры:
2. Далее фигуры начинают "расти", к фигурам добавляются новые клетки из числа еще не занятых:
3. Возможна ситуация, когда фигуре расти некуда - все соседние клетки уже заняты. Например, для красной фигуры:
4. Единственный выход - красная должна "отобрать" клетку у другой фигуры. Какую угодно отбирать нельзя. Знаком "+" помечены "критические" клетки - те, без которых фигура разваливается на несвязанные части. Их трогать запрещено.
Здесь красная фигура "отобрала" клетку у оранжевой, а оранжевая - у красной.
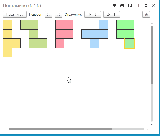
5. Далее красная фигура "отбирает" клетку у синей, и синяя восстанавливается до нужного размера.
Как видим, итераций до окончания может пройти достаточно много, до нескольких десятков (зависит от количества фигур). Но насколько надежен этот алгоритм? Можно ли быть уверенным, что он всегда завершиться с нужным результатом? К сожалению ,нет.
На первой картинке желтая и синяя фигуры не смогут "вырваться" с нижнего края. На второй картинке ни одна из фигур не сможет занять свободные, белые клетки.
Решением этой проблемы служит автоматический перезапуск алгоритма после некоторого числа итераций, например 100.
Головоломка тестировалась в тонком клиенте 8.3.22.1709.
Как всегда, приветствуются замечания / дополнения / комментарии.
Вступайте в нашу телеграмм-группу Инфостарт