Графин 7.7. (окончание)

29.11.10

Скачать файл

ВНИМАНИЕ: Файлы из Базы знаний - это исходный код разработки. Это примеры решения задач, шаблоны, заготовки, "строительные материалы" для учетной системы. Файлы ориентированы на специалистов 1С, которые могут разобраться в коде и оптимизировать программу для запуска в базе данных. Гарантии работоспособности нет. Возврата нет. Технической поддержки нет.

Наименование		По подписке [?]	Купить один файл
10Cv7.zip .zip 33,48Kb 45	45	Скачать (1 SM)	Купить за 1 850 руб.

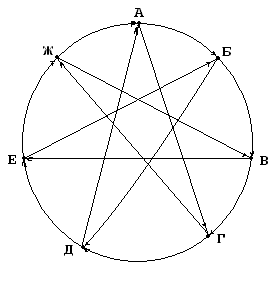
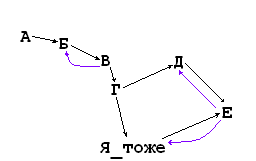
Предыдущие мои публикации Граф(ин) 7.7. и Граф(ин) 7.7. (дополнение) носили, скорее, умозрительный характер, имея одной из целей продемонстрировать, что деревья в частности и графы вообще вполне уживаются с семерочной платформой. Однако после появления статьи Запрос против рекурсии или "разузлование" номенклатуры мне просто некуда было деваться – и вот пришлось сваять небольшую конфигурацию для исследования «разузловательных» процессов. В конфигурации присутствуют два справочника: НоменклатурныеПозиции и Наборы. Содержимое справочника Наборы (с реквизитами Отец, Сын, Количество) как раз и определяет исследуемый граф.

Разумеется, я начал с

Тест № 1. "Десять" Справочник содержит 6-уровневый 10-арный граф , имеющий 1 000 000 различных ветвей и при обходе такого графа таблица ВремТаблица6 на выходе цикла алгоритма содержит 1 000 000 записей. Проще говоря, корневому элементу подчинены 10 элементов, каждому из которых подчинен одинаковый набор из десятка следующих элементов и т.д.

Ориентиром для меня служил пост № 118 из темы http://forum.infostart.ru/forum14/topic35991/ :

Через таблицу значений в 77 это сделать сложнее. У вас отсутствует команда НайтиСтроки , выбирающая по фильтру нужные строки из таблицы значений. Ну, раз взялся , то помни : - контроль зацикленности каждой ветки обязателен. 1. 4 мин - не о чем говорить 2. 3 мин - очень плохо 3. 2 мин - просто плохо 4. 1.5 мин - посредственно 5. 1 мин - хорошо 6. 40 сек - отлично 7. 20 сек - Арчибальд - СУПЕРСТАР на все времена ! ( в указанное время входит копирование элементов из справочника в таблицу значений)

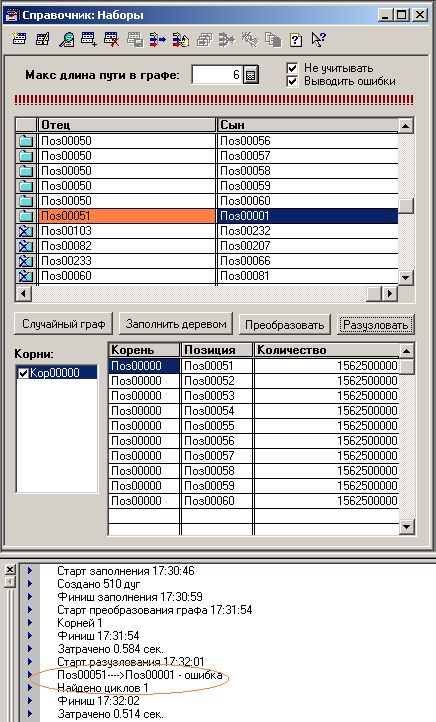
Ну, и сразу получил 0.777 секунды, из которых 0.5 - преобразование графа и 0.276 - собственно разузлование (скрин 1). Отнюдь не 20 сек, как в упомянутой статье. Но похуже, чем в статье Как не «попасть на миллион», решая задачу разузлования , хоть и не на два порядка.

Ладно, думаю, попробуем 100 000 000 (скрин 2). 0.993 секунды.

Добрался аж до 100 000 000 (скрин 3). 1.525 сек. То есть "деревья" (которые и не деревья вовсе, на самом-то деле) из Теста №1 обходить неинтересно.

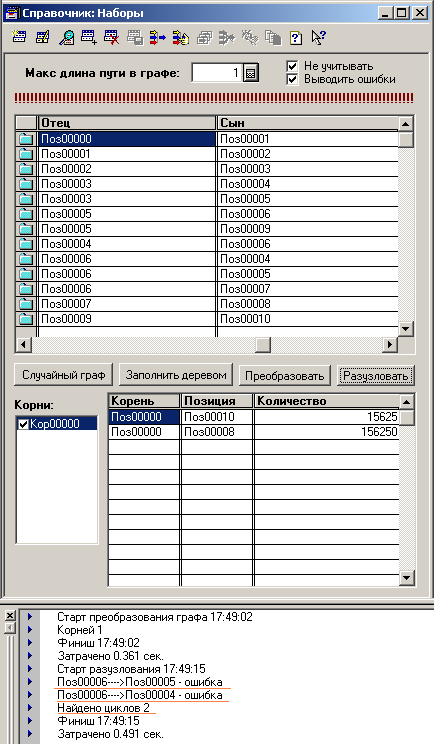
А вот заполнять список дуг (справочник Наборы) произвольным (псевдослучайным) образом, находить в полученном графе вершины, не имеющие родителей (корни), и разузловывать сразу все эти корни, либо несколько (по отметкам в списке корней) – достаточно познавательно (скрин 4). Все-таки 3.02 секунды. Правда, разузловывались десять позиций. Бывает и больше.

Все действия производятся в форме справочника Наборы. В частности, на форме кнопки для двух вариантов заполнения исходного справочника. Кнопка Преобразовать запускает конвертацию представления графа дугами в представление вершинами. Все коды открыты. В архиве – сохраненная конфигурация.

Попробуйте поиграться!

Ну и, наконец, вывод. Успешность (эффективность) решения задач весьма призрачно зависит от платформы. Зато сильно зависит от спроектированной структуры данных...

29.11.2010. Еще несколько слов о задаче разузлования. Теоретическая сложность этой задачи - О(N * lg N), где N - число (различных) узлов графа. Именно так вел бы себя алгоритм в упомянутой статье "Запрос против рекурсии...", если бы автор не отказался от конструкции "СГРУППИРОВАТЬ ПО" и не искал вместо ошибочной дуги графа все ошибочные цепочки, порожденные этой дугой. Применительно к задаче разузлования такой подход не учитывает наличия стандартизации узлов и деталей - а она реально существует. Гайка М10х17 - она и есть гайка...

+19 –

См. также

Экспорт нескольких MXL таблиц в один XLS файл, на отдельные листы. Простой алгоритм

Загрузка и выгрузка в Excel Математика и алгоритмы Программист Платформа 1С v7.7 Платформа 1С v8.3 Бесплатно (free)

Статья посвящена распространённому вопросу - как сохранить несколько таблиц (отчетов) в формате MXL, с которым работает 1С, на отдельные листы одного Excel файла. Освещается простой алгоритм решения проблемы штатными средствами, без использования внешних модулей и библиотек (не относящихся к 1С и Excel).

23.11.2015 19283 etmarket 14

.NET(C#) для 1С. Динамическая компиляция класса обертки для использования .Net событий в 1С через ДобавитьОбработчик или ОбработкаВнешнегоСобытия

Разработка внешних компонент Математика и алгоритмы Программист Платформа 1С v7.7 Платформа 1С v8.3 Бесплатно (free)

Динамическая компиляция класса обертки для использования .Net событий в 1С через ДобавитьОбработчик или ОбработкаВнешнегоСобытия, а так же генерация модулей на C# и 1С для подключения к событиям. Использование DynamicMethod и ILGenerator. Представлены примеры для использовании событий System.IO.FileSystemWatcher (Ожидает уведомления файловой системы об изменениях и инициирует события при изменениях каталога или файла в каталоге.) и SerialPort (обработка сканера штрих кода подключенного к COM порту). Обертка позволяет использовать классы .Net только на языке 1С. Реализация 1C Messenger описанного здесь http://infostart.ru/public/434771/

12.11.2015 51892 Serginio 36

Степень сходства двух наименований справочника

Математика и алгоритмы Программист Платформа 1С v7.7 Платформа 1С v8.3 Абонемент ($m)

Статья посвящена исследованию следующего вопроса: необходимо сравнить 2 наименования справочников с целью вычисления их степени сходства. По задумке, степень сходства должна выражаться в процентах.

1 стартмани

25.02.2015 25154 etmarket 46

Задача про сгибание листка

Математика и алгоритмы Программист Платформа 1С v7.7 Конфигурации 1cv7 Абонемент ($m)

Часто при приеме на работу встречается задача про сгибание листка

1 стартмани

26.02.2013 19803 11 Sbelyi78 38

Конструктор логиста

Управление взаимоотношениями с клиентами (CRM) Оптовая торговля Розничная торговля Математика и алгоритмы Программист Пользователь Оперативный учет 7.7 1С:Комплексная 7.7 1С:Торговля и склад 7.7 1С:Производство+Услуги+Бухгалтерия Розничная и сетевая торговля (FMCG) Транспорт, автопарки, такси Оптовая торговля, дистрибуция, логистика Управленческий учет Абонемент ($m)

Формирование маршрутов доставки на основе генетического алгоритма (решения задачи коммивояжера) для 1С Предприятия 7.7

1 стартмани

12.01.2013 29253 117 phsin 10

Универсальная печать таблицы значений

Математика и алгоритмы Системный администратор Программист Бухгалтер Оперативный учет 7.7 Бухгалтерский учет 7.7 Расчет 7.7 Конфигурации 1cv7 Россия Абонемент ($m)

Универсальная печать таблицы значений, которую не стыдно прикрутить к рабочей базе данных. Группировка данных, подсчет итогов, составление диаграмм, выгрузка в быстрый доступ к исходной ТЗ.

1 стартмани

23.05.2012 14902 66 McSeem 3

Обработка определения объема жидкости в цилиндрическом горизонтальном резервуаре

Математика и алгоритмы Разное Оперативный учет 7.7 Бухгалтерский учет 7.7 1С:Бухгалтерия 7.7 1С:Комплексная 7.7 1С:Торговля и склад 7.7 1С:Производство+Услуги+Бухгалтерия Россия Абонемент ($m)

Определение объема жидкости в цилиндрическом горизонтальном резервуаре измерением глубины жидкости

1 стартмани

03.04.2012 17288 5 akrazan 11

Тригонометрические функции в 7.7

Математика и алгоритмы Программист Платформа 1С v7.7 Конфигурации 1cv7 Россия Абонемент ($m)

Алгоритм получения значения тригонометрических функций путем разложения их в ряд Тейлора

1 стартмани

04.03.2012 8779 4 nysysimara 10

Комментарии

Подписаться на ответы Инфостарт бот

Свернуть все

1. ildarovich 7930 26.11.10 17:05 Сейчас в теме

Две просьбы:
1. Перепишите, пожалуйста, абзац с упоминанием моей статьи, а то с лету кажется, что описанное в моей статье решение занимает 20 секунд, хотя на самом деле результат правильной программы, описанной в моей статье - 0,122 секунды! Там же есть скриншот графа с 33-мя уровнями, который решается за 3,5 секунды. Разница между Вашими и моими результатами - в 5 раз (0,122 и 0,777). Это преимущества платформы. Могу обосновать.
2. Давайте называть вещи своими именами: в задаче, которую Вы решили за 0,777 секунды НЕТ ДЕРЕВА! Там есть граф из уровней с 0-го по 6-ой, вершины в смежных уровнях которого попарно связаны! В моей статье, есть рисунок этого графа, программа рисования которого на 8 занимает 10-ть строк! В ДЕРЕВЕ ветви принципиально не пересекаются! А вот преимущества запросов в немоей статье обосновываются их якобы хорошей работой для структур типа ДЕРЕВО. Там реально создаются в базе и связываются спецификациями 1 111 111 номенклатур. В том дереве 111 111 дуг! Но даже в этом случае реальные результаты рекурсии лучше!

2. Арчибальд 2709 26.11.10 17:17 Сейчас в теме

(1) Согласен. Подредактировал.

3. Арчибальд 2709 26.11.10 17:40 Сейчас в теме

(1) Кстати, рекурсия полностью эквивалентна "бесконечному" циклу. Рекурсивная процедура, вообще говоря, выглядит так:

Процедура Проц() 
   //что-то сделали, при этом изменилось контекстное окружение 
   Если ПораЗаканчивать Тогда 
      Возврат;//контекст - из стека 
   Иначе 
      Проц(); //контекст - в стек ОС 
   КонецЕсли; 
КонецПроцедуры

То же самое делает цикл

Пока 1=1 Цикл
   //что-то сделали, при этом изменилось контекстное окружение
   //возможно, потребуется "затолкать" это окружение в некий самодельный "стек"
   Если ПораЗаканчивать Тогда
   //возможно потребуется извлечение из стека
      Прервать;
   Иначе
      Продолжить;
   КонецЕсли;
КонецЦикла

Показать

Так что сравнивать имеет смысл Запрос vs Рекурсия/Цикл, а не Рекурсия vs Цикл

4. hogik 443 26.11.10 19:25 Сейчас в теме

(0)
Ставлю "плюс" на публикацию за сам алгоритм.
А с точки зрения СУБД доказано (показано), что много записей в БД - плохо, а мало - хорошо. А много бесполезных записей - очень плохо. Но это уже другая тема - тема про "запросы". ;-)

5. Ish_2 1112 27.11.10 20:21 Сейчас в теме

(4) Вы меня удивляете , Владимир. Вы ведь знаете эту задачу ,её цену и сами её решали. Человек щелкнул миллионный граф за секунду....
Вместо того, чтобы предостеречь Арчибальда - Вы его поощряете.
Я сейчас я ему вроде как конкурент, меня он не послушает , а Вы то что ?

6. hogik 443 27.11.10 23:21 Сейчас в теме

(5)
Игорь.
Я четко понимаю (знаю), что Александр решал совершенно другую задачу. И Сергей - другую. Но еще, я четко понимаю, что вы ставите и решаете "свою" задачу из-за отсутствия "нормальных" средств для её решения. Типа, жизнь заставляет.

ДалееРассуждизм.
Есть такое выражение: "Если изнасилование неизбежно, то надо расслабиться и получить удовольствие." Вы расслабились, получаете... ;-) Но это не означает, что следует пропагандировать такую схему получения "удовольствия". Т.к. на самом деле больше всего удовольствия получает "насильник". А Вы его поощряете к дальнейшим деяниям, подставляя множество очередных жертв. Соучастник, Вы - наш... ;-)
КонецРассуждизма.

Вот, написано:
"Успешность (эффективность) решения задач весьма призрачно зависит от платформы. Зато сильно зависит от спроектированной структуры данных..."(с)

Т.е. думать и работать надо. А не искать готовые решения, типа: 1С, 2С...nC...."СКД"...0С.
Я Вашу "деятельность" называю поиском "Волшебной палочки".
Но, это очень мягко сказано... :-( :-( :-(

7. Ish_2 1112 28.11.10 01:09 Сейчас в теме

Всё как обычно.Ок.

8. hogik 443 28.11.10 05:48 Сейчас в теме

(7)
Игорь.
А как может быть ещё?
Я ничего нового Вам сказать не могу.
Я задаю Вам вопросы - Вы не отвечаете.
Ну, хоть, в этой теме ответьте мне на простые вопросы.
Как дерево из 1111111 узлов может использоваться для описания "разузлования, спецификаций..." 60 изделий? Это специально под запросы и 20 секунд сделано?
И почему Вы никак не комментируете результат по скорости на задаче в 1111111 номенклатур? А значение на ADS-е без запросов 20-35 секунд в "файловом" режиме, и 60-70 секунд в клиент-серверном режиме, именно, для 1111111 номенклатур. И почему при написании этого моего алгоритма на языку 1С-а время становится за 200 секунд? Или Вам пояснить Вашу же фразу "...если реализовать задачу на Си или Delfi, то удастся достичь лучшего быстродействия, чем указано в теме ?"(с)
Эх...
P.S. Прощу прощения у Автора данной темы. Но меня, опять, возмутил призыв Игоря к объективности при сравнении "абсолютных величин"...

9. Ish_2 1112 28.11.10 07:51 Сейчас в теме

(8) Перескакивать не будем. Сначала разберемся с разработками Сергея и Арчибальда .
Там ,слава Богу, разговор пошел "узко-конкретный".

10. hogik 443 28.11.10 19:32 Сейчас в теме

(9)
Игорь.
"разговор пошел "узко-конкретный"."(с)
Да, уж... Очень - конкретный:
2 > 1 - верно.
2 грамма > 1 килограмм - ошибка.
2 грамма > 1 миллиметр - бред !!!
Сравнивайте решения для различных 1111111 номенклатур.
Или вернитесь к "изначальному" описанию схемы БД:
СвойID, РодительID, Количество, СсылкаНаНоменклатуру
Т.е. не извращайте схему БД под удобства решения частной задачи запросами.
Частных задач ("узко-конкретных") очень много - схем БД не напасётесь... ;-)
Извините. Повторяюсь. Всё написано в форуме ещё до публикации Ваше статьи. :-(

11. Ish_2 1112 28.11.10 19:42 Сейчас в теме

(10) Браво , Владимир !
Смотрите тему , развязка близка.

12. Арчибальд 2709 29.11.10 09:54 Сейчас в теме

Как моя оценка сложности/времени (N * lg N / 10000) сек. соотносится с реальностью для деревьев с уникальными узлами:
1<10<10<10<10<10<10 (~ 1 000 000 узлов) оценка 600 реальность 630
1<10<10<10<10<10 (~ 100 000 узлов) оценка 50 реальность 40
1<10<10<10<10 (~ 10 000 узлов) оценка 4 реальность 3.3
1<10<10<10 (~ 1 000 узлов) оценка 0.3 реальность 0.3
1<10<10 (~ 100 узлов) оценка 0.02 реальность 0.12

13. hogik 443 30.11.10 03:05 Сейчас в теме

(12)
Александр.
А Вы запустите свою программу под отладчиком.
И посмотрите на "качество" компиляции/интерпретации операторов 1С по времени. Не ввода/вывода, а умножения, деления, сложения, вызова функций, СоздатьОбъект() и т.д.
Эта скорость 30-и летней давности!!!
Я такую скорость имел на IBM/370 (Ряд 2, ЕС-1045).
Я замерял время выполнения инструкции: x=x+a[i]*a[i].
На "Си" это выполняется в 1000 раз быстрее чем на 1С.
А время ввода/вывода можете считать как, порядка, 30 секунд для чтения 1111111 записей по ключу. В случае DBF в локальном режиме, думаю, и того меньше.
И еще печальный факт про "1С 7.7".
Методы внешней компоненты вызываются медленнее чем родная функция 1С-а.
Т.е. если расчетные алгоритмы пытаться ускорить на ВК, то весь алгоритм в неё и придется помещать.

15. Арчибальд 2709 30.11.10 07:34 Сейчас в теме

(13)

А Вы запустите свою программу под отладчиком.

А что такое отладчик? © Вовочка :D

14. hogik 443 30.11.10 04:01 Сейчас в теме

(12)
+13
Думаю, в Вашем алгоритме поможет turbobl и пересоздание индексов.
Ну, а в сетевом режиме будет всё плохо.
Только "охват" транзакцией всего куска алгоритма в части чтения БД.

16. Ish_2 1112 30.11.10 11:54 Сейчас в теме

(0) Там , слава Богу, мы закончили. Теперь здесь на правах вольного стрелка :

Именно так вел бы себя алгоритм в упомянутой статье "Запрос против рекурсии...", если бы автор не отказался от конструкции "СГРУППИРОВАТЬ ПО" и не искал вместо ошибочной дуги графа все ошибочные цепочки, порожденные этой дугой. Применительно к задаче разузлования такой подход не учитывает наличия стандартизации узлов и деталей - а она реально существует. Гайка М10х17 - она и есть гайка...

Так вот оно что ! Я твой алгоритм не проверял , но теперь все понятно , как ты контролируешь зацикленность .

Секрет СУПЕРскорости представленных обработок один -
отказ от надежного гарантированного контроля зацикленности каждой ветки.
К чему это приводит - почитай в теме "Запрос против.." , чем закончились тестирование обработки Сергея на зацикленность.
Ведь если бы Сергей исправил вторую ошибку - я бы подросил ему уже заготовленную третью.. И латал бы он свой СУПЕРбыстрый алгоритм до бесконечности.
Если у тебя в алгоритме нет надежного контроля зацикленности ,
то ты тоже мог оказаться в положении Сергея : то ли
- признать ненадежность своего алгоритма и тогда все предыдущие утверждения , СУПЕРхарактеристики , сравнительные таблицы полетят в тартарары
- то ли ли просто прекратить разговор дескать Нет ! и всё.

Так вот .
"СГРУППИРОВАТЬ ПО " не применяется в алгоритме именно потому , что нужно контролировать КАЖДУЮ ВЕТКУ графа. Применение этой опции приводит к резкому ускорению в тесте №1 (тот самый опрометчивый "щелчок за секунду" как в товей обработке) , но потере контроля зацикливания каждой ветки.

17. Арчибальд 2709 30.11.10 13:21 Сейчас в теме

(16) У меня есть контроль зацикленности. Для каждого узла проверяется, не пересекаются ли множества его предков (всех) и "сыновей". Контроль абсолютен.

18. Ish_2 1112 30.11.10 13:45 Сейчас в теме

(17) Если у тебя контроль абсолютен , то ты не можешь применять ".Свернуть(...)" для промежуточной таблицы - ты потеряешь ветки для контроля и тогда непонятно твоё выступление по поводу "СГРУППИРОВАТЬ ПО".

19. Арчибальд 2709 30.11.10 14:33 Сейчас в теме

(18) "Сгруппировать по" у меня в кавычках. Я группирую перечень предков узла.
Т.е. как бы для ТЗ с колонками "Узел","СписокПредков" делаю ТЗ.Свернуть("Узел","СписокПредков"). Реально так:

Для ы = 1 по ТекСписок.РазмерСписка() Цикл
ТекЗнач = ТекСписок.ПолучитьЗначение(ы);
Если ПромРез.СписокПредков.НайтиЗначение(ТекЗнач) = 0 Тогда
ПромРез.СписокПредков.ВставитьЗначение(ы,ТекЗнач);
КонецЕсли;
КонецЦикла;

20. Ish_2 1112 30.11.10 15:42 Сейчас в теме

(19) Вот тебе и поспорить с Владимиром. У него ведь тоже 77.
И он-то реализовал миллионный граф 1-10-10-10-10-10-10 с уникальными узлами за 180+-40 сек ,
а у тебя 600 сек. Разница впечатляет.

21. Ish_2 1112 30.11.10 17:59 Сейчас в теме

(19) У тебя ПромРез имеет два поля Узел,СписокПредков.
Пусть в твоей таблице ПромРез колонка СписокПредков - это строка (у меня это "СтрокаКодов") и тогда ТекСписок содержит строковые коды справочника+ символ разделителя:

Для ы = 1 по ТекСписок.РазмерСписка() Цикл
ТекЗначКод = ТекСписок.ПолучитьЗначение(ы);
Если Найти(ПромРез.СписокПредков,ТекЗначКод) = 0 Тогда
ПромРез.СписокПредков = ПромРез.СписокПредков+ТекЗначКод;
КонецЕсли;
КонецЦикла;

Если так ,то не быстрее ли ?

23. Арчибальд 2709 01.12.10 08:00 Сейчас в теме

(21) Оптимизацией я не занимался вообще. Возможно, ты прав.

22. Ish_2 1112 01.12.10 07:59 Сейчас в теме

(0) Виноват. Только сейчас прочитал содержание темы. Читал и хмыкал.
Погнавшись за званием
7. 20 сек - Арчибальд - СУПЕРСТАР на все времена !

ты попал в ловушку. И влетел на 10 мин. в главном тесте.

24. Арчибальд 2709 01.12.10 09:22 Сейчас в теме

(22) Черта с два. Прочитай еще раз твой текст теста №1 -

каждому из которых подчинен одинаковый набор из десятка следующих элементов и т.д.

- там я в секунду уложился, т.е. в 20 раз лучше, чем с твоими запросами ;) . А специально под конкретный граф "заточки" не было - алгоритм универсален.

25. Ish_2 1112 01.12.10 09:24 Сейчас в теме

(24) Прочитай еще раз (22).

26. Ish_2 1112 02.12.10 09:27 Сейчас в теме

Арчибальд , скачал твою конфигурацию - сижу тыкаюсь...
Ты мне скажи сколько зацикливаний определит твоя программа для нижеследующего графа.

Прикрепленные файлы:

32. Ish_2 1112 02.12.10 11:07 Сейчас в теме

Теперь я ничего не понял. Ты о чем ?

У меня на рисунке в (26) нарисовано дерево -
совершенно стандартный во всех пакетах мира вид.

Элемент "ОшГ000001" имеет двух детей : "ОшД0000001" и "Я зациклен..." и так далее.
У меня один простой вопрос : сколько, каких зацикленных элементов (или ветвей) покажет твоя программа ?

80. Ish_2 1112 06.12.10 08:47 Сейчас в теме

Начало дискуссии положил пост (26),задающий начальный пример

В (37) ты пишешь ссылась на (26):

А гшраф, нарисованный здесь опять-таки, по моему варианту даст 1 (дугу), по твоему алгоритму - 5 (позиций в "дереве"), а по соображениям из (35)долже бы дать 2 (вершины).

Это и послужило пружиной, толчком ко всей дальнейшей дискуссии.
Теперь же у тебя алгоритм выдает 2 дуги.

81. Арчибальд 2709 06.12.10 09:18 Сейчас в теме

(80) Ссылаясь на (26), я написал в (37):

На картинке в 26 посте у тебя 6 красных строчек. Не 2 - по числу ошибок. И не три - по числу вершин, входящих в циклы.

Т.е. я указал, что ошибочных дуг в графе из (26), по моим подсчетам, две. И в (34) я это говорил. И в (59).

Ты же цитируешь из 37 поста ту часть, которая к 26-му отношения не имеет, а относится к другому графу, там же и изображенному. Этот граф имеет одну ошибочную дугу - это по-моему. А по-твоему - пять ошибочных цепочек.

82. Ish_2 1112 06.12.10 09:54 Сейчас в теме

(81) Не люблю незаконченных дел.
У тебя сделана обработка "для сэбэ", заранее предполагая что тестировать её никто не будет.
Попытавшись интерактивно что-то создать в твоём справочнике я только чертыхался.
Если ты действительно хочешь узнать правду , насколько твой алгоритм надёжен.
Создай удобный интерфейс для проверки при помощи элемента дерева формексом или еще как.

Посмотри как сделано у меня :
Пользователь может без труда интерактивно задать любой граф, используя дерево.
Тут же проверить и увидеть ПОЛНЫЙ граф ошибок (см. 26).
Обработка в таком виде уже используется в УПП с легкими исправлениями.
Посмотри http://forum.infostart.ru/forum24/topic36726/message402436/#message402436

Я веду речь о том , что твою и мою обработки нужно выровнять по функционалу. В таком виде как у тебя - они не сопоставимы.

P.S. Важность тестирования любого утверждения явно вытекает из моей темы :
все рассуждалки...
соображения и размышлизмы...
цифирьки о сверхскоростях ...
разлетелись в дребезги после проверки.

83. Арчибальд 2709 06.12.10 10:57 Сейчас в теме

(82) Обработка у меня выложена. Код открыт. Ошибок не найдено. Все тесты прогнаны. То есть о моем алгоритме известно все.
Теперь касательно твоей обработки. Она не прошла тест из 50-го поста (текстуально он продублирован как Тест № 1А в посте 69). Я уже не говорю, что тест на 10 миллиардов (как Тест № 1, только вместо 6 поколений 10) она вообще не сможет пройти. Вот где-то здесь несопоставимость функционала и проглядывает.

Пользователь может без труда интерактивно задать любой граф, используя дерево.
Тут же проверить и увидеть ПОЛНЫЙ граф ошибок (см. 26).

Поздравляю Вас, гражданин, соврамши © Коровьев
Что увидит пользователь на тесте № 1А "Десять+ошибка"? Да ничего!
И поясни мне, каков будет процесс интерактивного задания графа с картинки ниже.

Прикрепленные файлы:

84. Ish_2 1112 06.12.10 11:10 Сейчас в теме

(83) Не спеши.
Так мы закончили рассматривать твою обработку ?
Ты считаешь , что пользователь должен лезть в код чтобы задать нужную ему ошибку зацикливания ?
И этого достаточно :

Обработка у меня выложена. Код открыт. Ошибок не найдено. Все тесты прогнаны. То есть о моем алгоритме известно все.

Кем не найдено ? - Тобой ?
Кем прогнаны ? - Тобой ?
Известно всё , кому ? - Тебе ?

Я тебе как раз и толкую о том , что автор разработки САМ должен создать удобный интерфейс
для проверки правильности своих суждений. Чтобы пользователь САМ интерактивно мог всё проверить и смоделировать ситуацию. У тебя этого просто нет.

И все твои утверждения повисают в воздухе - кто полезет ковыряться в чужом коде ?

86. Арчибальд 2709 06.12.10 12:47 Сейчас в теме

(84) При чем здесь спешка? Это ведь ты написал

Посмотри как сделано у меня :
Пользователь может без труда интерактивно задать любой граф, используя дерево.
Тут же проверить и увидеть ПОЛНЫЙ граф ошибок (см. 26).

Вот я и говорю: покажи. Не буду же я покупать БП или УПП, чтобы взглянуть. Ты покажи, я тебе на слово поверю.
И касательно удобного интерфейса для построения графов. Куда уж удобнее: вля каждой дуги указать начало, конец, количество (последнее - только для разузлования). Нет и не может быть других интерфейсов для "произвольных графов, заданных таблицей наборов {Отец, Сын, Количество}" - именно таким было твое начальное условие. Ну, а то, что в восьмерке есть встроенный объект "дерево", как в формексе, ничего не прибавляет к твоему алгоритму разузлования.
Ты обыгран на твоем поле и по твоим правилам - если в качестве правил брать условия задачи из твоей статьи, а не из комментариев к моей. Доказательство: Добавление всего одной ветки к твоему Тесту №1 ставит тебя в тупик. Это не висящее в воздухе, а твердо опирающееся на факты утверждение.

97. hogik 443 06.12.10 18:07 Сейчас в теме

(82)
"Я веду речь о том , что твою и мою обработки нужно выровнять по функционалу. В таком виде как у тебя - они не сопоставимы."(с)
Гениально!
Тема, плавно, перешла в обсуждение интерфейса. Цвет обсуждать будем? ;-)
Игорь.
Вы уже себе доказали, что любую постановку задачи следует подгонять под доступные средства (инструменты) программисту. Что еще может сделать Ваш алгоритм с "деревом" кроме проверки циклов и подсчета "изделий"? Это всё, что требуется для "разузлования"?

98. Ish_2 1112 06.12.10 18:11 Сейчас в теме

(97) Ладно , Владимир. Пустой спор.

99. hogik 443 06.12.10 18:22 Сейчас в теме

(98)
Игорь.
Спор - с кем?
Лично, я с Вами не спорю. ;-)
Я Вам задаю вопросы.
Вы мне не отвечаете. :-(

27. Арчибальд 2709 02.12.10 10:20 Сейчас в теме

Если граф такой, как на рисунке (твою табличку не очень понимаю) - найдет одну ошибочную ветку (выделена цветом

Прикрепленные файлы:

28. Арчибальд 2709 02.12.10 10:26 Сейчас в теме

На таком - тоже одну

Прикрепленные файлы:

29. Арчибальд 2709 02.12.10 10:26 Сейчас в теме

А на таком - две

Прикрепленные файлы:

30. Арчибальд 2709 02.12.10 10:34 Сейчас в теме

А на таком - 4

Прикрепленные файлы:

31. Арчибальд 2709 02.12.10 10:46 Сейчас в теме

Я понял! Тебя интересует такая ситуация, как на картинке. Мой ответ - 2. А вот у тебя, похоже, побольше :D

Прикрепленные файлы:

33. Ish_2 1112 02.12.10 11:22 Сейчас в теме

Или полсмотри как это выглядит в твоем справочнике :

Прикрепленные файлы:

38. Ish_2 1112 02.12.10 15:02 Сейчас в теме

Виноват не объяснил.
Это картинка из моей программы рисующей граф ошибок ,
на котором завалился Сергей . На красный цвет не нужно обращать внимание.

Давай для простоты ориентируйся только на (33) - это практически тот же граф , но в табличном виде .

Итак , в (33) - наш граф. А (35) - все соображения по раскрутке этого графа.
Корень в графе - один . Это позиция номенклатуры с именем "Корень". (33)
Идя последовательно от "Корень" по таблице Справочника (33) мы вытащим всю цепочку.
в (35) показано , что всех возможных ветвей для позиции номенклатуры "Корень" может быть 4.
И далее по тексту (35). Ты согласен с этими рассуждениями ?

А ты изобрази своим рисунком граф в (33).

39. Арчибальд 2709 02.12.10 15:29 Сейчас в теме

(38) См. картинку из (34) без А, Б, В (т.е. Корень - это Г).

40. Ish_2 1112 02.12.10 16:15 Сейчас в теме

(39)
В машине рисунков нету. Нужно последовательно обойти весь граф (34)
побывав в каждом узле и построив все возможные ветки.
Двигаемся по одинарной ветке , пока не сработало зацикливание.
Напоминаю, зацикливание есть факт нахождение на любой из веток от корня до вершины двух одинаковых элементов.
Все ! такие факты мы должны выявить.

Начинаем движение вслепую.

Ветка 1. А-Б-В- Г- Я_тоже - Е - Я_ТОЖЕ. На последнем сработало зацикливание , движение прекращаем.

Ветка 2. А-Б-В- Г- Я_тоже - Е - Д - Е.

Ветка 3. А-Б-В- Г- Д - Е - Д.

Ветка 4. А-Б-В- Г- Д - Е - Я_Тоже - Е

Итого З элемента (Е- дважды)

И число 3 и состав Е,Д,Я_тоже НЕ ЗАВИСИТ от порядка обхода.

Если же мы начнем хитрить при обходе то потеряем элемент.

48. Арчибальд 2709 03.12.10 08:54 Сейчас в теме

(40)

Начинаем движение вслепую.

Я не хочу вслепую. Начинать движение имеет смысл от тех узлов, которые не имеют предков. А если таких узлов нет, значит в графе полный бардак: Все узлы расположены на путях, содержащих циклы. Идем от корня.

Шаг 1. (А)(А-Б). Норма.
Шаг 2. (А,Б)(Б-В). Норма.
Шаг 3. (А,Б,В)(В-Г). Норма.
Шаг 4. (А,Б,В,Г)(Г-Д)(Г-Я_тоже). Норма.
Шаг 5. (А,Б,В,Г,Д,Я_тоже)(Д-Е)(Я_тоже-Е). Норма.
Шаг 6. (А,Б,В,Г,Д,Е,Я_тоже)(Е-Д)(Е-Я_тоже). Две ошибочные дуги. Их и отмечаем как ошибочные в справочнике дуг (исходном или его копии) Больше ошибок в справочнике (графе) нет.

И число 3 и состав Е,Д,Я_тоже НЕ ЗАВИСИТ от порядка обхода.
Если же мы начнем хитрить при обходе то потеряем элемент.

Обойди "бесхитростно" граф на рисунке, начиная с узла Е (Г,Д,Я_тоже). Не получается? Правильно, начиная откуда попало, ориентированный граф не обойдешь. Т.е. твой алгоритм точно так же зависит от порядка обхода, как и мой - только я это заранее предусмотрел, и не позволяю начинать откуда попало.

В машине рисунков нету

А как же http://infostart.ru/public/78976/ ;)

Прикрепленные файлы:

49. Ish_2 1112 03.12.10 09:19 Сейчас в теме

(48)
А я тебе еще раз говорю : ты должен выдать весь список зацикленных элементов.
Ты мне сказал ДВА.
Я тебе говорю ТРИ !
и спрашиваю : Чем Я_тоже - хуже(лучше) чем Е и Д.
Или Чем Е хуже (лучше) , чем Я_Тоже и Д ?
Соображения как мы обходим граф, какие там дуги, когда в нем бардак или нет не имеют никакого смысла.

Еще раз : зацикливание есть факт нахождения на одной элементарной(одинарной) ветке графа одного и того же элемента в качестве "ребенка" и "родителя".
Точка.
"Вынь и положь" такие факты на стол. Любым способом !
Этот факт обнаруживается в текущем графе для ТРЕХ элементов. Е,Д,Я_ТОЖЕ.
Этот способ я описал.

Какой в этом практический смысл и что это дает ?

Исправить ошибку зацикливания не так-то просто - пользователю нужны ВСЕ зациклившие элементы, которые должны быть отображены на графе. Ему нужно видеть полную картину , как у тебя на рисунке , только подсвечены красным цветом Е,Д, Я_ТОЖЕ.
Чтобы выдать эту полную картину , мы должны иметь все три элемента и все их ветки.

P.S. Я тебе обойду граф с любого места (получу два графа : "все родители" и "все потомки") . Могу и с Е.

Другими словами, ты идешь в своих рассуждениях от программиста, от того , как удобно обходить граф,
А я иду от пользователя , ему удобнее видеть ВСЕ зацикленные элементы.

50. Арчибальд 2709 03.12.10 09:40 Сейчас в теме

(49)

А я тебе еще раз говорю : ты должен выдать весь список зацикленных элементов.

Это у тебя юношеский максимализм :D
Берем граф из знаменитого теста № 1 и добавляем одну ошибочную дугу (см. рис.). При поиске циклов я одну дугу и найду - это то, что я реально должен. А ты найдешь 10 000 цепочек. То-то обрадуется твой пользователь ;).
Даже если ты выдашь ему список из 42 узлов - мало не покажется. Все равно это необозримо, и значит, бесполезно. Мы же прикладную задачу решаем, а не абстрактную.

Пишите, Шура, запросы. Внутри они золотые © Паниковский

Прикрепленные файлы:

52. Ish_2 1112 03.12.10 09:48 Сейчас в теме

(50) Я записал в красную книжицу : "4. обозвал Балагановым".

Конечно , ты старый и умный.. хихикаешь над нами , над молодежью.
Так вот, я тебе с юношеским максимализмом толкую :
программа обработки графа должна зафиксировать ВСЕ факты зацикливания,
а как их потом будет обрабатывать пользователь или промежуточная программа представления ошибок
- это не её ума дело. Зафиксируй и полоЖь !

54. Арчибальд 2709 03.12.10 09:59 Сейчас в теме

(52)

промежуточная программа представления ошибок

Еще и отдельную программу представления ошибок приплел :D Будь проще, и люди к тебе потянутся. Есть справочник дуг (больше, по твоему условию, нет ничего), пометил в нем ошибочные на удаление - вот и все представление.

55. Ish_2 1112 03.12.10 10:15 Сейчас в теме

(54) Ага, приплел. В моей обработке она есть.
А как бы я тогда анализировал ошибки , подбрасывал Сергею то одно ,то другое ?

Или как пользователь проверит что ты написал в своей теме ?
Да, мало ли что можно в "теме" намолоть ?
Скажи как я проверю , что то ,что ты написал в своей теме правильно ?
правильно ли ищутся ошибки зацикливания ? правильно ли обсчитывается огромный граф ? как ?
У тебя такой процедуры - нет . И пользователь поощряет тебя вслепую.
"Арчибальд...а, ну это хороший человек и про граф вроде неплохо пишет..! "

На рисунке представление обработки ошибок из ЗапросПротивРекурсии.epf

Прикрепленные файлы:

57. Арчибальд 2709 03.12.10 11:05 Сейчас в теме

(55) Берем граф из (50) и получаем картинку, внятно описывающую ситуацию. И разузлование прошло с игнорированием ошибочной дуги. Это называется практика.
Сейчас нарисую граф совсем уж конкретно такой, как ты хочешь.

Прикрепленные файлы:

58. Ish_2 1112 03.12.10 11:18 Сейчас в теме

(57) Арчибальд , я не смог ничего проверить и сымитировать в твоей программе.
Никаких средств контроля правильности обработки графа для пользователя не существует.
Вспоминал 77,тужился , пыжился , чертыхался..
Потом плюнул и написал тебе (26) , дескать скажи как оно будет ?
Давай лучше по рисункам графа. Стрелочки , картинки..

51. Арчибальд 2709 03.12.10 09:47 Сейчас в теме

(49)

Я тебе обойду граф с любого места (получу два графа : "все родители" и "все потомки") . Могу и с Е.

В тебе я не сомневаюсь. А вот твоя обработка ЗапросПротивРекурсии не обойдет.

53. Ish_2 1112 03.12.10 09:53 Сейчас в теме

(51) Обработка ЗапросПротивРекурсии.epf работает только в одну сторону ищет "детей".
Поэтому обойдет и получит только граф детей для Е.

Е-Д-Е
Е-Я_Тоже-Е

73. hogik 443 03.12.10 18:43 Сейчас в теме

(49)
Игорь.
Вы пишете: "...зацикливание есть факт нахождения на одной элементарной(одинарной) ветке графа одного и того же элемента в качестве "ребенка" и "родителя". "(с)
Но Ваш алгоритм это делает не в графе, а в "дереве".
Я Вам представил простейший алгоритм для решения задачи для "дерева". Хотя для "дерева" поиск циклов - это... ;-)
Вы "забраковали" мой алгоритм.
Почему?
А потому, что в моём решении нет ключевых, для Вас слов - "решить задачу надо запросами". И о чём тогда разговор в данной теме про "графины"? Давайте я Вам расскажу - почему очень многие задачи не следует решать запросами. Но это совсем другая тема - эта тема про запросы... ;-)

34. Арчибальд 2709 02.12.10 11:32 Сейчас в теме

Понял. Ответ - 2. Не 4!
Суть в том, что ты из графа делаешь дерево, дублируя подграфы, а я работаю с произвольным графом непосредственно. Только в качестве начальной выбираю вершину, не имеющую предков.

Прикрепленные файлы:

35. Ish_2 1112 02.12.10 13:31 Сейчас в теме

Что такое АБСОЛЮТНЫЙ КОНТРОЛЬ ?
Разложим граф на элементарные ветки
(пытаемся двигаться от корня по каждой ветке,пока по ней и только по ней, не встретим зацикливания) :

1. Корень -  КОшД01         - КошЕ01 - КОшД01                    - зациклен элемент "КошД01"
2. Корень -  КОшД01         - КошЕ01 - К я зациклен !   - КошЕ01 - зациклен элемент "КошЕ01" 
3. Корень -  К я зациклен ! - КОшЕ01 - КОшД01           - КошЕ01 - зациклен элемент "КошЕ01" 
4. Корень -  К я зациклен ! - КОшЕ01 - К я зациклен !            - зациклен элемент "К я зациклен !"

Вопрос : А с чего это я взял , что именно так жестко нужно проходить от корня - по каждой ветке
и не используется пред . информация о том что какой-то элемент зациклен ?
А с того, что в таком случае мы не зависим от порядка обхода графа и выдаем ПОЛНУЮ(всю) информацию о зацикливаниях в виде дерева(графа).
Как только мы начинаем использовать пред. информацию о зацикливании, то в попадаем зависимость от порядка обхода графа. И начинаем выдавать разный состав зацикленных элементов в зависимости от порядка обхода.
А это полная жуть ! Поиграйся порядком пунктов обхода 1-2-3-4, 4-3-2-1 и т.д. , учитывая пред.зацикливания, и получишь разный состав зацикленных элементов.

Поэтому НУЖЕН АБСОЛЮТНЫЙ КОНТРОЛЬ !
И правильный ответ - 3 элемента. Только 3 элемента дают полную постоянную информацию о зацикливании.
Как граф не обходи -получишь 3 элемента.

37. Арчибальд 2709 02.12.10 14:21 Сейчас в теме

На картинке в 26 посте у тебя 6 красных строчек. Не 2 - по числу ошибок. И не три - по числу вершин, входящих в циклы.
А гшраф, нарисованный здесь опять-таки, по моему варианту даст 1 (дугу), по твоему алгоритму - 5 (позиций в "дереве"), а по соображениям из (35)долже бы дать 2 (вершины).
И насчет начала обхода. Мой алгоритм выявляет все возможные корни (стартовые для разузлования) и позволяет "с кнопки" находить все ошибочные дуги.
Наконец, о безызбыточности. Ты все время говорил, что вся информация о графе должна содержаться в ТЗ {Отец,Сын,Количество}, т.е. в перечне дуг графа. Если даже поиск циклов дает тебе перечень узлов - куда ты его денешь? У меня все ясно: помечу на удаление ошибочный элемент (или даже обнулю поле Количество) и продолжу работу. В конце концов, исходной задачей было разузлование, а не раскрашивание "дерева" из найденных в графе путей.

Прикрепленные файлы:

36. Ish_2 1112 02.12.10 13:53 Сейчас в теме

Продолжим.
У тебя , Huse, Сергея - контроль зацикливания относительный (облегченный).
Отсюда и СУПЕРскорости . Если попытаться организовать такой надежный контроль в ваших алгоритмах - то всё.
Всему КОНЕЦ.
Конец скорости, конец надежности
(памяти клиента может и не хватить для хранения стольких строк(веток) графа).
Таков мой скромный прогноз.

41. Ish_2 1112 02.12.10 16:33 Сейчас в теме

Так вот я храню ВСЕ ветки 1-4. И по ним в любой момент могу построить ВЕСЬ граф на котором отображу ошибки для пользователя и он их быстро найдет.
Исправить сложные ошибки зацикливания - не так-то просто. У меня пользователь получит полную картину, где что лежит и что с чем связано. Вы граф не храните : у вас два элемента Е и Д НИЧЕГО не дадут пользователю и он полностью не увидит всю картину зацикливания. Т.е. функционал у меня в сто раз выше чем у тебя или Сергея .
Мало того , на больших объемах еще и обгоняет вас всех по скорости.

42. hogik 443 02.12.10 18:37 Сейчас в теме

(41)
"Так вот я храню ВСЕ ветки 1-4. И по ним в любой момент могу построить ВЕСЬ граф на котором отображу ошибки для пользователя и он их быстро найдет."(с)
А если пользователей много? И они "в любой момент..."(с) ;-)
Игорь.
Ваш алгоритма не будет работать в "теме" СУБД.
Т.к. СУБД придумали не для удобства программиста писать запросы (отчеты).
А для обеспечения множества пользователей (алгоритмов) достоверной информацией из БД.
Ну не годятся "регистры накопления" для задач "разузлования". ;-)

43. Ish_2 1112 02.12.10 18:48 Сейчас в теме

(42) Попытаюсь объяснить .
В начале обработки , копируется из базы Справочник (ВЕСЬ!) СпецификацииНоменклатуры во временную таблицу "Спецификации". На время копирования можно блокировать Справочник от изменений (пример демо и этого не показано). В дальнейшем работа идет только с временной таблицей. И никакие пользователи не мешают.

Необходимость блокирования Справочника на время исполнения всей обработки в статье не рассматривается вовсе.
Это отдельная тема другого разговора. В статье рассматривается узкий вопрос "алгоритм разузлования", сопутствующие вопросы не рассматриваются вовсе.

45. hogik 443 02.12.10 19:42 Сейчас в теме

(43)
1) "рассматривается узкий вопрос"(с)
Тогда уберите в свой статье фразы типа:
"На предприятиях ,осуществляющих сборку"(с)
"доходить в реальных задачах"(с)
"самый быстрый, надежный" (с)
"в статье идет речь не о "заточке" для тестов №1 и № 2, а об универсальной обработке"(с)
"достаточно для создания надежного и эффективного механизма "разузлования""(с)
"она более технологична и надежна"(с)
И т.д.
2) "В дальнейшем работа идет только с временной таблицей. И никакие пользователи не мешают."(с)
Ага. ;-)
Они просто работают с разными исходными данными. Один скопировал во временную таблицу. Работает. Другой пользователь уже "поработал" и начал менять исходную таблицу. А тут подоспел результат второго пользователя. И...
3) "Необходимость блокирования Справочника на время исполнения всей обработки в статье не рассматривается вовсе."(с)
Т.е. этой "необходимости" нетУ ??? ;-)
4) "Это отдельная тема другого разговора."(с)
Нет. Игорь. Эта не отдельная тема. Т.к. скорость выполнения алгоритма - это одна из многих характеристик алгоритма. И, далеко, не первая характеристика. Но любой алгоритм в "теме" многопользовательских СУБД ОБЯЗАН обеспечивать достоверность данных для ВСЕХ пользователей. Или "потребитель" системы будет решать задачу бесконечной "консолидации документов" даже в рамках ОДНОЙ подсистемы. И если "алгоритм" не обеспечивает требуемой достоверности, то это не алгоритм, а НЕЧТО. Но работает оооо-чень быстро. ;-)
5) "Попытаюсь объяснить"(с)
Игорь. Еще раз вынужден Вам ответить и на эту фразу.
Объясните ЭТО себе!!!

46. Ish_2 1112 02.12.10 19:52 Сейчас в теме

(45) Всё будет хорошо, Владимир.
Давайте не портить тему Арчибальду. Ок.

44. Ish_2 1112 02.12.10 19:01 Сейчас в теме

(0) Саша, в (41) гордыня обуяла. Виноват.

47. hogik 443 03.12.10 05:23 Сейчас в теме

(0)
Александру, про "отладчик". ;-)
Две программы.
Первая загружает в справочник "дерево" с 1111111 вершинами, из теста #1 от Игоря.
Вторая выполняет обход дерева рекурсивным методом с анализом циклов ;-) и подсчетом количеств "изделий". Каждая программа выполнялась три раза. Система 1С 7.7 на DBF, локально, монопольно. Но, в конфигурации определено 1007 таблиц. И одинаковое дерево представлено трижды. По файлу 1Cv7.DD - таблица "ДеревоА" на 8-ом месте, "ДеревоБ" на 508-ом месте, "ДеревоВ" на 1007-ом месте. Остальные таблицы БД - пустые.
Времена загрузок "дерева":
ДеревоА 148 сек.
ДеревоБ 615 сек.
ДеревоВ 1083 сек.
Времена обходов "дерева":
ДеревоА 194 сек.
ДеревоБ 673 сек.
ДеревоВ 1136 сек.
А мы тут про "графины" разговариваем... :-(
P.S. В комплексной конфигурации многие "боевые" таблицы находятся в конце файла DD.
P.P.S. При проведении тестов вентилятор процессора ревел на полную мощность. ;-)

56. Ish_2 1112 03.12.10 10:41 Сейчас в теме

Вообщем , я в своей теме написал уже. Надеюсь тебе понравилась вся эта история..

59. Арчибальд 2709 03.12.10 11:18 Сейчас в теме

Вот

Прикрепленные файлы:

60. Ish_2 1112 03.12.10 12:29 Сейчас в теме

(59) У тебя изумительный(!) есть рисунок проясняющий суть наших разногласий.

1. Допустим , обработка дошла до Б-В и говорит тебе человеческим голосом :
"Арчибальд , это зацикливание дальше нет смысла искать..
да и запутаться можем.. там сам черт ногу сломит !".
Ты как культурный человек и говоришь ей (тоже человеческим голосом) :
"Хорошо , родная , дальше не пойдем !"
И загрустил Арчибальд,так как увидел только одну ветку-обрубок : А-Б-В.

2. Допустим , обработка дошла до Б-В и говорит мне человеческим голосом :
"Ish_2 , это зацикливание дальше нет смысла искать..
да и запутаться можем.. там сам черт ногу сломит !".

Я ей говорю запросто :
"Молчи , дура ! Твоё дело искать ! "
И пошла она дальше , и нашла все ветки и принесла мне их.
Я и выбрал ,что и как показать на экране , а что не показывать.
Смотри ниже , что я увидел :

Прикрепленные файлы:

61. Арчибальд 2709 03.12.10 13:16 Сейчас в теме

(60) Да ничего похожего. Спокойно помечает (исключает) ошибочную ветку и дальше движется. С разузлованием правильной части.

Прикрепленные файлы:

62. Ish_2 1112 03.12.10 13:40 Сейчас в теме

(61)
Нет , Арчибальд , не отпирайся !
Главный художественный смысл - робость перед обработкой передан верно.
А где ты оробел то ли в Б-В , то ли на кольце Г-Д-Е-Я_ТОЖе - это детали.

Теперь конкретно :
ТЫ не ПОСТРОИЛ КОЛЬЦО ! У тебя только 3 зацикленных элемента.
Ты не выдал все 4(четыре) зацикленных элемента.
Байка - верна.

63. Арчибальд 2709 03.12.10 14:44 Сейчас в теме

(62) Это уж вообще бред какой-то.
Ты все время талдычишь, что я не сделал того или другого. Я утверждаю, что делать это мне здравый смысл не позволяет, ты же мне - забудь, мол про здравый смысл, делай как я сказал.
Вот цитируем тебя

И загрустил Арчибальд,так как увидел только одну ветку-обрубок : А-Б-В.

2. Допустим , обработка дошла до Б-В и говорит мне человеческим голосом :
"Ish_2 , это зацикливание дальше нет смысла искать..
да и запутаться можем.. там сам черт ногу сломит !".

Я ей говорю запросто :
"Молчи , дура ! Твоё дело искать ! "
И пошла она дальше , и нашла все ветки и принесла мне их.

Первое утверждение опровергнуто картинкой в 61 посте. Граф полностью пройден, отмечены все ветки, приводящие к зацикливанию, разузлование корректного подграфа проведено.
Займемся утверждением "и нашла все ветки и принесла мне их". Понятно, что оно ложно в части "ВСЕ". Не найдено бесконечное количество веток:
А-Б-В-Б-В
А-Б-В-Б-В-Б
А-Б-В-Б-В-Б-В
А-Б-В-Б-В-Б-В-Б
А-Б-В-Б-В-Б-В-Б-В
...
Обработка твоя может, конечно, сказать что-то типа "тут мы уже не первый раз ходим, зациклились" - но это уже будет элемент здравого смысла, т.е. вроде бы западло для тебя. Значит, должен сказать "молчи, дура, еще не все ветки построены".
Возьми, нарисуй свою картинку для гафа из 37 поста - и все понятно будет...
А еще лучше - вот для этой картинки отработай. Выдай пользователю 16 дуг, 9 вершин и 8 цепочек.

Прикрепленные файлы:

64. Ish_2 1112 03.12.10 15:56 Сейчас в теме

(63)

Ты все время талдычишь, что я не сделал того или другого. Я утверждаю, что делать это мне здравый смысл не позволяет, ты же мне - забудь, мол про здравый смысл, делай как я сказал.

Ммм... ну, талдычу.
Это такой способ("наезд"), попытка сблизить наши здравые смыслы , э... предложение взаимопонимания.

Первое утверждение опровергнуто картинкой в 61 посте.

Подтверждаю. Твоя обработка пройдет Б-В . Правда застрянет на кольце.
Сильно не придирайся к неточностям в байке.Она же - байка.

Займемся утверждением "и нашла все ветки и принесла мне их". Понятно, что оно ложно в части "ВСЕ". Не найдено бесконечное количество веток:

Ну, разумеется, не все. Ты очень , очень строг к художественной байке .
Конечно, речь идет о движениях по веткам до первого зацикливания.
И тогда всё становится понятно.

Прикрепленные файлы:

65. Арчибальд 2709 03.12.10 16:11 Сейчас в теме

(63)

Подтверждаю. Твоя обработка пройдет Б-В . Правда застрянет на кольце.

Опять ложь. Мой алгоритм никогда не застревает. Он фиксирует все случаи, когда потомок узла встречается в перечне предков, и все случаи, когда начало и конец дуги совпадают. Он строит максимально возможный подграф без циклов и разузловывает его.
Приведенная картинка показывает, что дляграфа с одним циклом из двух узлов твой алгоритм находит три ошибки. Вполне очевидно, что такой алгоритм корректным считаться не может.

66. Ish_2 1112 03.12.10 16:25 Сейчас в теме

А вот и самый первый пример. Как обработка ЗапросПротивРекурсии.epf
представила пользователю первый граф.

Прикрепленные файлы:

67. Ish_2 1112 03.12.10 16:56 Сейчас в теме

Опять ложь. Мой алгоритм никогда не застревает.

"Застревает" - это значит не проходит и не показывает все зацикленные элементы .
Напоминаю, зацикливание есть факт когда в графе один элемент и "родитель" и "ребенок".
Ты не все такие факты определяешь - значит, именно застреваешь.

Приведенная картинка показывает, что для графа с одним циклом из двух узлов твой алгоритм находит три ошибки. Вполне очевидно, что такой алгоритм корректным считаться не может.

Может , Арчибальд, может.
После прохождения обработки я имею таблицу со строковой колонкой "СтрокаКодов" и три записи в ней:
А-Б-В-Г-В
А-Б-В-Г-В
А-Б-В-Г-В

Только по этой таблице и надо ориентироваться. Подчеркиваю, по ней и только по ней.
Эта информация служит исходной для визуального построения дерева.
Из неё мы получаем :
Фактов зацикливания обнаружено 3.
Различных Элементов зацикливания - 1.

Как уж изобразить это на экране - это мой вопрос. Как хочу так и рисую.
Что нужно показать пользователю ?
Если факты зацикливания, то с этой точки зрения картинка правильная.
Если максимально сжатое изображение то

Прикрепленные файлы:

69. Арчибальд 2709 03.12.10 17:38 Сейчас в теме

(67)

Еще раз. Зацикливание есть факт, когда ребенок числится среди предков отца (перечень предков включает и самого отца). Такой (и только такой) ребенок считается незаконным. Мой алгоритм находит всех таких детей (и выводит на печать вместе с отцами. Определяются все факты появления дуги, приводящей к зацикливанию.
Ну, а все цепочки предков, приводящие к отцу незаконного ребенка, остаются при этом вполне легитимными - соответственно, в перечень ошибок попадать не должны.

Для восстановления равенства (с учетом того, что я тебе сообщил свои результаты на твоих тестах) предлагаю тебе прогнать мой
Тест № 1А. "Десять+ошибка"
Справочник "СпецификацииНоменклатуры" содержит 6-уровневый 10-арный граф , имеющий 1 000 000 различных ветвей и при обходе такого графа таблица ВремТаблица6 на выходе цикла алгоритма содержит 1 000 000 записей. Но сам справочник "СпецификацииНоменклатуры" в своей табличной части содержит лишь 60 записей.
Проще говоря , корневому элементу подчинены 10 элементов, каждому из которых подчинен одинаковый набор из десятка следующих элементов и т.д.
"+ошибка" - это еще одна дуга, ведущая с 6-го уровня на 1-й

Ну и результаты сообщить, конечно. Мои прилагаю.

Прикрепленные файлы:

70. Ish_2 1112 03.12.10 18:03 Сейчас в теме

(69) Арчибальд , давай так. По порядку.
Предки , дети , зациленности...

Я собираюсь доказать , что слово "застревает" здесь самое точное.
Это значит , что если твой алгоритм не показывает все связи для графа (68) ,
то слово "застревает" - здесь самое точное !

Действительно , Дано :
есть граф (68) описан нами на рисунке и в табличной форме.
Ничего запретного в нем - НЕТ. Он вполне реален.

Теперь мы говорим обработке - обойди его , мы хотим его увидеть.
А твоя обработка говорит :
Не-А. Дальше кольца я не пойду , не хоцца - там сложности!

Что имеем ? Имеем Реальный граф - и имеем обработку, которая его полностью
не обойдет и не покажет нам его !
А зачем нам такая обработка , Арчибальд? Какой в ней прок ?
Это покажу , это не покажу...

Обработка должна обойти весь граф , зафиксировать все зацикленности.
А что делать , с этой информацией , как её интерпретировать - это не ёё ума дело !
Поэтому фраза из байки "Молчи , дура ! Твоё дело - искать !" - более чем оправдана.

И сама байка (60) несет в себе четкий , неискажающий сути проблемы смысл.

68. Ish_2 1112 03.12.10 17:17 Сейчас в теме

Слово "застревает" - здесь точное, на мой взгляд.
Т.е. у меня алгоритм "прёт во все щели" - он не интеллектуальный.
И в этом его сила. Нашлась связь - зацикливания нет - значит можно "переть" дальше.
Поэтому он и обходит больше ветвей , чем твой.

Вопрос для твоего алгоритма , появились новые ветки в графе- какие из них определит твой алгоритм :
Просьба по "буквам" показать путь прохождения твоего алгоритма , как идет движение и где стопорится.

Прикрепленные файлы:

71. Арчибальд 2709 03.12.10 18:25 Сейчас в теме

(68) Да пожалуйста. Только не смогу показать где стопорится - нет такого места.
Итак, А=0,Б=1,В=2,Г=3,Д=4,Я_тоже=5,Е=6,Ж=7,З=8,И=9,К=10 (в смысле, Поз00010 на скрине).

По шагам (вызовам следующего уровня): слева список предков, справа - дуги-дети
1. (0)(0-1)
2. (0,1)(1-2)
3. (0,1,2)(2-3)
4. (0,1,2,3)(3-4)(3-5) детей теперь двое, так что шаг в две строчки будет
5. (0,1,2,3,4) (4-6)
(0,1,2,3,5) (5-6)(5-9) В этом поколении уже трое детей
6. (0,1,2,3,4,6) (6-4)(6-5)(6-7)
Фиксируем ошибочную дугу (6-4)и разрываем ее
(0,1,2,3,5,6) (6-7)(6-5) Дуги (6-4) уже нет!
Фиксируем ошибочную дугу (6-5) и разрываем ее.
Свертывем предков 7-го в один список (0,1,2,3,4,5,6,7)
(0,1,2,3,5,9) (9-10)
7. (0,1,2,3,4,5,6,7) (7-8)
(0,1,2,3,5,9,10)
8. (0,1,2,3,5,6,7,8)

Прикрепленные файлы:

72. Ish_2 1112 03.12.10 18:30 Сейчас в теме

(71) Э... это что ? Нехорошо, Арчибальд, смеяться ..

76. ildarovich 7930 04.12.10 14:04 Сейчас в теме

(71) Александр!
Желаю успехов разорвать, наконец, все ошибочные связи в рассуждениях Игоря.
Хотя у нас похожие подходы и выводы, возможно, мое понимание проблемы чем-то Вам поможет.
1. Игорь ошибочно считает, что контроль зацикленности - это перечисление всех циклов. Поскольку множество циклов - подмножество путей,
то задача оказывается NP-полной. Вы, как и я, понимете, что Заказчика интересует не миллион циклов, а неупорядоченное множество вероятно-ошибочных дуг,
которые нужно перечислить и дать на проверку оператору. Эта задача гораздо проще - в наихудшем случае сплошной зацикленности будет выдан полный список дуг,
существенно (слабо сказано!) более короткий, чем полный список путей. Также как если бы в IQ-тесте человека спрашивали: какая цифра в перечне кажется лишней,
а он отвечал бы перечнем чисел, содержащих ошибочные цифры!

Вроде бы все просто, да не очень! Есть пример, из-за которого Игорь "не доезжает".
Есть ациклический орграф (гамак): А->В, А->Г, Б->В, Б->Г, В->Д, В->Е, Г->Д, Г->Е. Если зациклить его дугой Е->Б, то Ваша обработка выдаст (и исключит) дуги Б->В, Г->Е (могу ошибиться).
Этот список не содержит действительно ошибочной дуги: Е->Б! Простой выход здесь в том, чтобы при обнаружении цикла в Вашем (и моем) алгоритме включить в
список подозрительных все дуги обнаруженного цикла, даже, если они окажутся потом лишними. Это не скажется на быстродействии и, возможно, будет последним аргументом
в пользу кодинга!

Я (в своем алгоритме) не спешу этого делать и вот почему: это не моя задача и не мой Заказчик. Для своего Заказчика я бы разработал специальный алгоритм, который позволил
бы указать место ошибки с максимальной точностью (найти минимальный разрез, делающие граф ациклическим). Идею этого алгоритма я изложил в теме Игоря (пост #177).
Сейчас не могу сказать, но, возможно, есть и более простой метод.

2. Мне кажется, что Игорь нечетко разделяет понятия графа и дерева. Для него граф - это такое компактное (и неудобное) представление дерева, вроде формулы
или теста для проверки "настоящих", "боевых" графов - деревьев. Хотя в жизни (но не в программах!) деревья встречаются гораздо реже. Видимо, занятия программированием,
анализ таких структур как справочники, интерпретация вложенных циклов, левого соединения в запросах, дали ему такое искаженное представление действительности. Из-за этого
он и проверяет свою и наши обработки прежде всего на деревьях, в результате чего результаты сравнения оказываются необъективными.

77. hogik 443 05.12.10 00:06 Сейчас в теме

(76)
Сергей.
Извините, вмешаюсь.
Вы пишите: "Игорь ошибочно считает, что контроль зацикленности - это перечисление всех циклов."(с) А я думаю, что Игорь ошибочно считает, что "контроль зацикленности"(с) является самой важной составляющей в обсуждаемых алгоритмах. Т.к. слово "цикл" - это единственный термин объединяющий обсуждаемые (разные!!!) задачи, проблемы, решения...
Игорь, в моём понимании, поставил вопрос - как обойти дерево минимальным количеством запросов и перенести хоть что-то из дополнительных (надуманных) действий с узлами дерева, на сервер. Обязательно - дерево! Обязательно - запросами! Обязательно - на сервер!
Больше Игоря ничего не интересует. Печально... И, чего мы обсуждаем?

74. Ish_2 1112 03.12.10 18:53 Сейчас в теме

Арчибальд, перенесем на воскресенье ? Время 18-50 .Идет ?

75. Ish_2 1112 03.12.10 19:02 Сейчас в теме

Мда.. Успел только посмотреть мельком . Как же я это проверю ?
С Сергем было проще , я рисовал искусственные кольца в справочнике , какие хочешь - легко.
И сразу проверял результат. А тут... мамочки.

78. Ish_2 1112 05.12.10 12:19 Сейчас в теме

Арчибальд, все мои рассуждения относились к какой-то другой версии.
Скачал последнюю сегодня, но она отличается от старой которая была у меня.
Ведь мы же спорим именно о твоей текущей конфигурации.
Всё-таки лучше было меня явно предупредить о всех изменениях в твоей конфигурации с момента публикации.

На всякий случай,
сразу после опубликования я в свой файл обработки одно изменение Добавил колонку "Количество" на панели Спецификации.
Убрал лишнюю строку НачДата = Текущаядата(); И всё!
Как только началось тестирование в моей теме мой файл обработки неизменен как скала.
Алгоритм у меня не менялся вовсе с момента публикации.
Все мои утверждения о своей обработке касались именно этого неизменного алгоритма,
к тому же опубликованного основном тексте темы.
Если бы пришлось внести в него какие-то изменения - я бы обязательно объявил об этом всем собеседникам.

79. Арчибальд 2709 06.12.10 08:32 Сейчас в теме

(78)

Конфигурация, приведенная здесь, алгоритмически не менялась с момента публикации за исключением добавления двух "галочек "Не учитываль", т.е. не ограничиваться заданной длиной цепочек, и "Выводить ошибки" - печатать/не печатать перечень ошибочных дуг.

Ведь мы же спорим именно о твоей текущей конфигурации.

Вот именно. Странно было бы здесь спорить о конфигурации из предыдущей публикации, которая демонстрировала поведение алгоритма нахождения корректных цепочек максимальной длины в случайных графах.
(76) У меня нашлись бы дуги Б-В и Б-Г. ;) А подход у нас, естественно, похож, только я ищу не минимальный корректирующий разрез, а строю максимальное по количеству поколений семейство потомков выбранного предка. Да к тому же, позволяю выбирать в качестве "патриархов" только тех, кто предков не имеет. Таким образом, при появлении в Вашем примере дуги Е-Б я увижу, кроме появления двух ошибочных дуг, еще одно событие: исчезновение узла Б из списка патриархов.

85. Ish_2 1112 06.12.10 11:37 Сейчас в теме

+84 Прежде чем предлагать другому тест при сравнительном анализе ,
ты должен показать другому тест на своей обработке:
ВОТ ОНО ! СДЕЛАЙ КАК У МЕНЯ !

Как я проверю правильность создания хотя бы одной ветки в твоём тесте 10-10-10-10-10-10..., интерактивно ?
Как внесу туда нужную ошибку ?
У меня это делается так : последовательно открываешь нужную ветку и видишь какие там элементы и сколько их ? Интерактивно открываешь часть графа (спецификацию) и правишь её .
То есть я не требую от тебя такого чего нет у меня самого.

Еще и еще раз повторяю если хочешь меряться - создай удобный интерфейс проверки твоей обработки.
Без этого ты можешь утверждать что угодно - НИКТО В ТВОЙ КОД проверять не полезет.

87. Арчибальд 2709 06.12.10 13:08 Сейчас в теме

(85) Порверить меня легко, без залезания в код. На форме нажимаем кнопку "Заполнить деревом" - и прямо на той же форме списка в справочнике видим искомые 510 дуг. Это не миллион веток, как у тебя, это обозримо. Внести одну ошибку, как я предлагаю, - это внести одну строчку в список, 511-ю. Скрин в 69 посте легко воспроизводится.
Покажи мне картинку (твое дерево) для графа из 83-го поста. Я не требую от тебя ничего такого, чего у тебя, по твоим утверждениям, нет. Я даже не буду выяснять, как ты строил картинку. Короче, сделай хоть что-нибудь помимо безответственного трепа.

88. Ish_2 1112 06.12.10 13:21 Сейчас в теме

Демо БП не нужно покупать. Покупается только платформа 1с8.
Посмотри сценарий. Здесь мы не делаем никакого разузлования.
Только смотрим и корректируем то , что создано тестом № 2

Прикрепленные файлы:

89. Ish_2 1112 06.12.10 13:29 Сейчас в теме

Добавляю : в обработке помимо разузлования - создан специальный интерфейс , который позволяет без разузлования корректировать, просматривать,
Справочник СпецификацииНоменклатуры ( у тебя это "Отборы").

90. Ish_2 1112 06.12.10 13:47 Сейчас в теме

Продолжаю. Обладая таким интерфейсом - за 15 мин я интерактивно создам такие кольца - ловушки , в т.ч. и звезды , что тебе и не снилось.
После запуска разузлования - тут же проверю у себя правильно ли сформировался Граф ошибок .
См.ниже
Заметь : пользователь имеет не обрубок какой- то ветки а ВЕСЬ ГРАФ , т.е. информацию удобную для анализа.
И тут же можно исправить ошибку или внести новую.

Прикрепленные файлы:

91. Арчибальд 2709 06.12.10 14:21 Сейчас в теме

(90)

Обладая таким интерфейсом - за 15 мин я интерактивно создам такие кольца - ловушки , в т.ч. и звезды , что тебе и не снилось.

Много не надо. Мне достаточно звездочки из 87 поста. А ты все с деревьями только носишься.
Задача была не в создании доп. интерфейса работы со справочником, а в разузловании. Эта задача на твоих тестах у меня решается на порядок быстрее, чем у тебя. А отобразить заодно "дерево разузлования" - это вообще смехотворное дополнение.

92. Ish_2 1112 06.12.10 14:54 Сейчас в теме

Понял. Разница в подходах к задаче - колоссальная.

Для меня - это прежде всего технологичное функциональное решение - рабочее место для человека , занимающегося спецификациями в реальной конфигурации, например БП 2.0. Первое требование - здесь простота и надежность контроля и доп.функционал.

Для тебя же - это прежде всего решалка тестов №1 и №2, а доп.функционал - это так для галочки.

Пожалуй при такой разнице в подходах - сравнительный анализ и правда невозможен.

93. Арчибальд 2709 06.12.10 15:14 Сейчас в теме

(92) Ничего похожего. Покажи мне простоту контроля в твоей обработке на тесте 1А. Ну, хотя бы работоспособность.
Первое требование всегда - работоспособность. Именно в этом разница в подходах заключается. У тебя же все технологично (правда, без ответа на вопрос из 83 поста), но на реальном небольшом графе с 511 дугами не работает.
Без твоего сообщения о результатах теста 1А я вынужден констатировать, что твоя обработка, возможно, способна отловить ошибки на графе с десятком дуг, но в боевых условиях непригодна.

94. Ish_2 1112 06.12.10 15:28 Сейчас в теме

(93) У меня уже есть именно такой тест № 3. Посмотри на верзнем рисунке в (88).
Сейчас пришлю отчет в скриншотах.

95. Ish_2 1112 06.12.10 15:36 Сейчас в теме

Вот и сам отчет.Ты всегда можешь обратиться к любому восьмерочнику.
Он с легкостью нажмет две кнопки и получит результат. Он у меня равен 19 сек.

Но нужно добавить.
Во временной таблице после окончания работы "разузлования" у меня хранятся ВСЕ ошибочные ветки.
Но Количество ошибок выдаваемых пользователю на монитор у меня ограничено - 100 ошибок.
Безболезненно можно увеличить до 1 000 шт. Только зачем ?

Прикрепленные файлы: