Вводная часть
В данной статье будет рассмотрен алгоритм, лежащий в основе работы любой схемы распределения затрат (СРЗ). В теории графов затрат этот алгоритм называется алгоритмом R-S-B, он определяет общие правила распределения потоков вторичных затрат на выходе любого центра затрат в Графе затрат. Для понимания работы этого алгоритма необходимо знать зачем в теории графов затрат выделяют потоки первичных и вторичных затрат, какие у них особенности и чем они отличаются друг от друга. Поэтому в первой части статьи коротко напомним этот раздел теории графов затрат.
Первичные и вторичные затраты
Понятия потоков первичных затрат и потоков вторичных затрат или далее для краткости просто первичных и вторичных затрат входят в перечень ключевых понятий теории графов затрат, поэтому их обычно изучают в первую очередь до изучения остальных свойств Графов затрат.
К первичным затратам относят затраты, стоимость которых можно определить непосредственно в момент совершения фактов хозяйственной жизни (ФХЖ). Поскольку ФХЖ должны оформляться первичными учетными документами – ведомостями начисления заработной платы или амортизации, актами выполненных работ и т.п., то можно сказать, что стоимости первичных затрат указываются в первичных учетных документах. Проще говоря, стоимости первичных затрат всегда известны до начала процедуры закрытия затрат периода (решения СЛАУ). С точки зрения теории графов затрат первичные затраты поступают на входы центров затрат не от других центров затрат, а от специфических узлов Графа затрат, не являющихся центрами затрат.
В том числе к классу первичных затрат относятся также и затраты, связанные со списанием в производство материалов (Дт20-Кт10). При списании материалов по себестоимости каждой единицы стоимость первичных затрат известна сразу. При использовании, например, скользящего FIFO или средней себестоимости для определения стоимости первичных затрат необходимо провести соответствующий расчет, но все равно эти стоимости можно определить до момента выполнения процедуры закрытия затрат периода (решения СЛАУ).
Вторичными затратами будем называть только те затраты, которые поступают в центры затрат от других центров затрат Графа затрат. Непосредственно в момент совершения ФХЖ (например, выпуска продукции на склад Дт43-Кт20) известно только количество вторичных затрат (готовой продукции), стоимость же вторичных затрат будет определена только в конце периода в результате выполнения процедуры закрытия затрат периода (решения СЛАУ). Можно сказать, что эта процедура перераспределяет заранее известную стоимость первичных затрат между всеми центрами затрат, и это перераспределение происходит с помощью потоков вторичных затрат.
Использование термина вторичные затраты не означает, что у экономического субъекта появляются помимо первичных затрат еще какие-то дополнительные затраты. Стоимость первичных затрат по-прежнему характеризует реальную стоимость ресурсов экономического субъекта и в этом смысле в процессе расчета себестоимости никаких дополнительных стоимостей вторичных затрат не возникает. Термин вторичные затраты просто удобно использовать для описания процедуры перераспределения первичных затрат между центрами затрат при расчете себестоимости.
Не может быть вторичных затрат без первичных затрат, стоимости вторичных затрат являются производными величинами от стоимостей первичных затрат. В качестве визуального образа для понимания ситуации можно представить стеклянную колбу, в которую наливают жидкости красного, зеленого и синего цветов (RGB). В зависимости от их пропорций внутри колбы можно получить смесь любого цвета. В этом визуальном образе исходные жидкости (RGB) можно ассоциировать с первичными затратами, а полученную смесь – со вторичными затратами.
Поясним вышесказанное на примере.
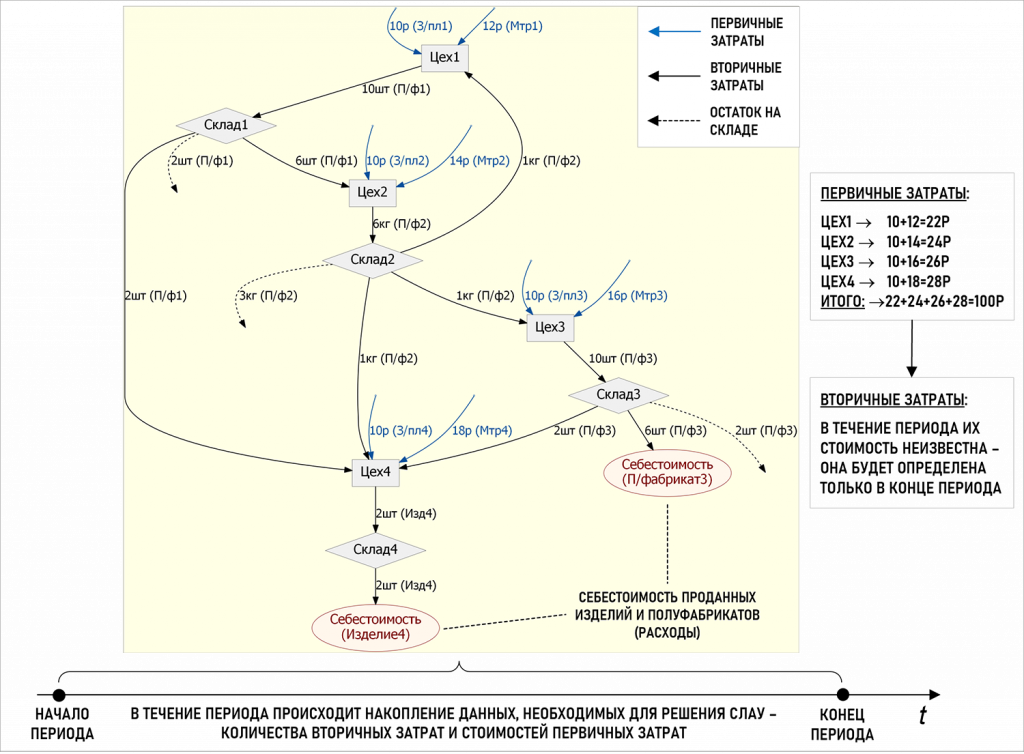
На рисунке показана модель экономического субъекта, производящего и продающего изделия и полуфабрикаты. Все четыре цеха получают первичные затраты (синие стрелки), стоимость которых должна быть известна до начала решения СЛАУ. Синие стрелки «входят» в центры затрат, а начинаются на специфических узлах, не являющихся центрами затрат. Состав первичных затрат в примере ограничен затратами на заработную плату и материалы. Эти затраты могут возникать в любой момент времени от начала до конца периода, но для расчета себестоимости за период важны только общие стоимости накопленных за период первичных затрат. Общая стоимость всех первичных затрат составила 100 рублей. При расчете себестоимости накопленная стоимость первичных затрат будет перераспределена между центрами затрат Графа затрат с помощью потоков вторичных затрат.
Вторичные затраты показаны на рисунке черными стрелками (дугами) с весами, обозначающими пока только количество полуфабрикатов и изделий. В отличие от первичных затрат потоки вторичных затрат всегда связывают между собой центры затрат. Для того, чтобы показать в графическом виде всю доступную информацию, на рисунке с помощью пунктирных стрелок (дуг) у складов показаны остатки на конец периода произведенных за период полуфабрикатов. В качестве весов пунктирных дуг показаны также только количества полуфабрикатов, так как это тоже вторичные затраты, стоимость которых определится в конце периода по результатам решения СЛАУ.
Необходимо напомнить, что теория математического моделирования относит СЛАУ к классу статических математических моделей, описывающих равновесные (установившиеся) режимы работы моделируемых систем, в нашем случае экономических (микроэкономических) систем, называемых экономическими субъектами. Использование СЛАУ в качестве математической модели означает, что в этой модели фактор времени не учитывается, то есть время t не является в ней независимой переменной. Что из этого следует?
Во-первых, как уже было сказано, для расчета себестоимости за период важны только общие стоимости накопленных за период первичных затрат. Внутри периода игнорируется вся хронология ФХЖ, то есть не имеет значения в какой момент времени были, например, произведены начисления заработной платы и списаны материалы в производство.
Во-вторых, точно также игнорируется и хронология ФХЖ в части вторичных затрат. Неважно в какой момент времени внутри периода вторичные затраты ушли из центра затрат или поступили в него, например, когда была произведена и поступила на склад готовая продукция и когда она ушла со склада. Важны только общие количества вторичных затрат и маршруты их движения по Графу затрат. Как следствие, реальные Графы затрат редко когда имеют строго древовидную структуру, обычно обязательно возникают так называемые контуры встречных затрат или просто встречные затраты, что совершенно нормально для такой модели.
Выше на рисунке можно выделить контур встречных затрат Цех1→Склад1→Цех2→Склад2→Цех1. Это можно объяснить тем, что, например, в начале периода Цех1 получил часть полуфабриката П/ф2 в составе первичных затрат (поступили от контрагентов) и использовал его для производства полуфабриката П/ф1, а в середине периода Цех1 использовал для своей работы уже полуфабрикат П/ф2, произведенный Цехом2 в этом же периоде. В данном случае пример моделирует условную ситуацию, поэтому вопросы технологии производства здесь подробно не рассматриваются.
Как видим, в хозяйственной реальности движения полуфабрикатов в контуре встречных затрат не были одномоментными, они происходили в разные моменты времени внутри периода. Но поскольку статическая модель расчета себестоимости на основе СЛАУ фактор времени внутри периода не учитывает, то в итоге получился контур встречных затрат, как будто все ФХЖ произошли в один и тот же момент времени. Что кстати совершенно не помешает далее рассчитать себестоимость с помощью СЛАУ.
Иногда пытаются избавиться от контуров встречных затрат и «откорректировать» Граф затрат таким образом, чтобы он имел строго древовидную структуру, причем изобретают для этого довольно сложные алгоритмы. Но возникает вопрос – зачем это делать? В чем смысл решения такой задачи? Ведь модель на основе СЛАУ является статической, где принципиально не учитывается фактор времени, и наличие контуров встречных затрат является прямым следствием этой особенности модели. Поэтому «корректировать» структуру Графа затрат, пытаясь удалить контуры встречных затрат, возникшие как раз из-за игнорирования фактора времени, в данном случае совершенно нелогично.
Скорее здесь можно предложить разработать другую модель, например, на основе обыкновенных дифференциальных уравнений, где время t используется в качестве независимой переменной. Возможно, тогда получится создать уже не статическую, а динамическую модель движения затрат «внутри» экономического субъекта. Но пока таких моделей не предложено, так что остается работать со статической моделью на основе СЛАУ со всеми ее особенностями. Не зря же существует устойчивое словосочетание – расчет себестоимости за период, то есть именно за период, а не в каждый момент времени. Так что статическая модель на основе СЛАУ со всеми своими особенностями имеет пока полное право на существование.
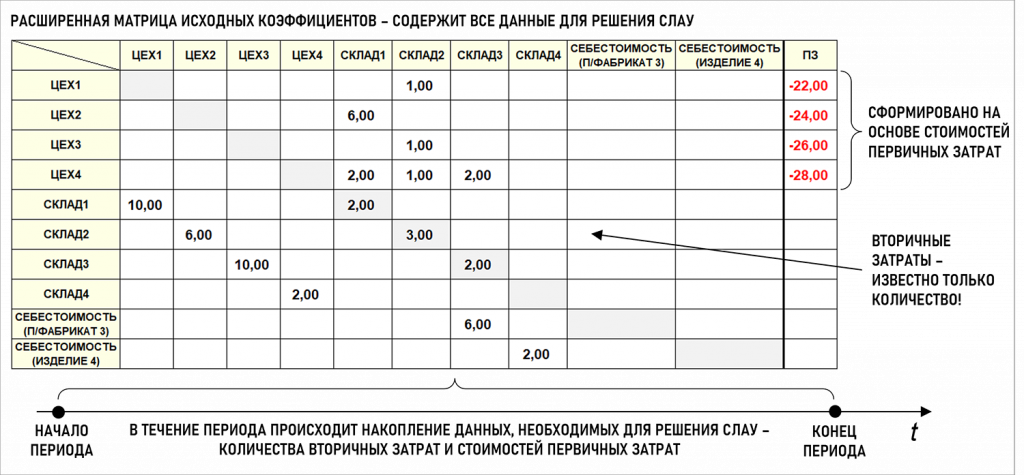
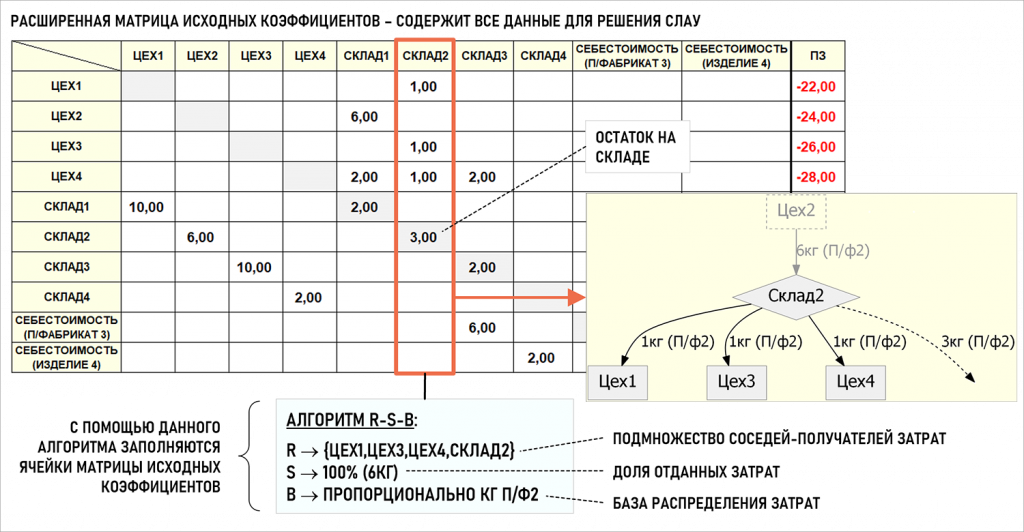
Но вернемся к нашему примеру. Расширенная матрица исходных коэффициентов для Графа затрат выглядит следующим образом:
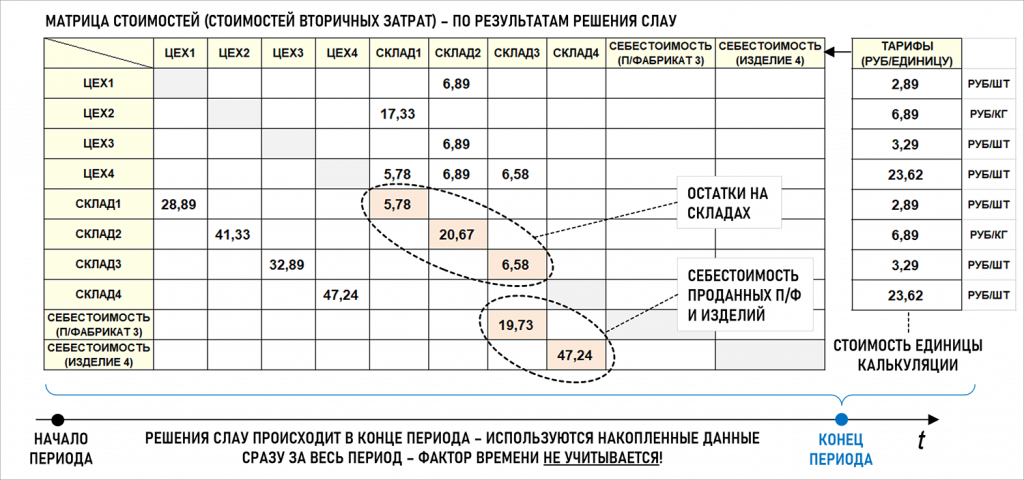
Решив в конце периода СЛАУ, определим тарифы – стоимости единиц калькуляции на выходе каждого центра затрат и найдем стоимости вторичных затрат (причем контур встречных затрат никак не помешал расчету):
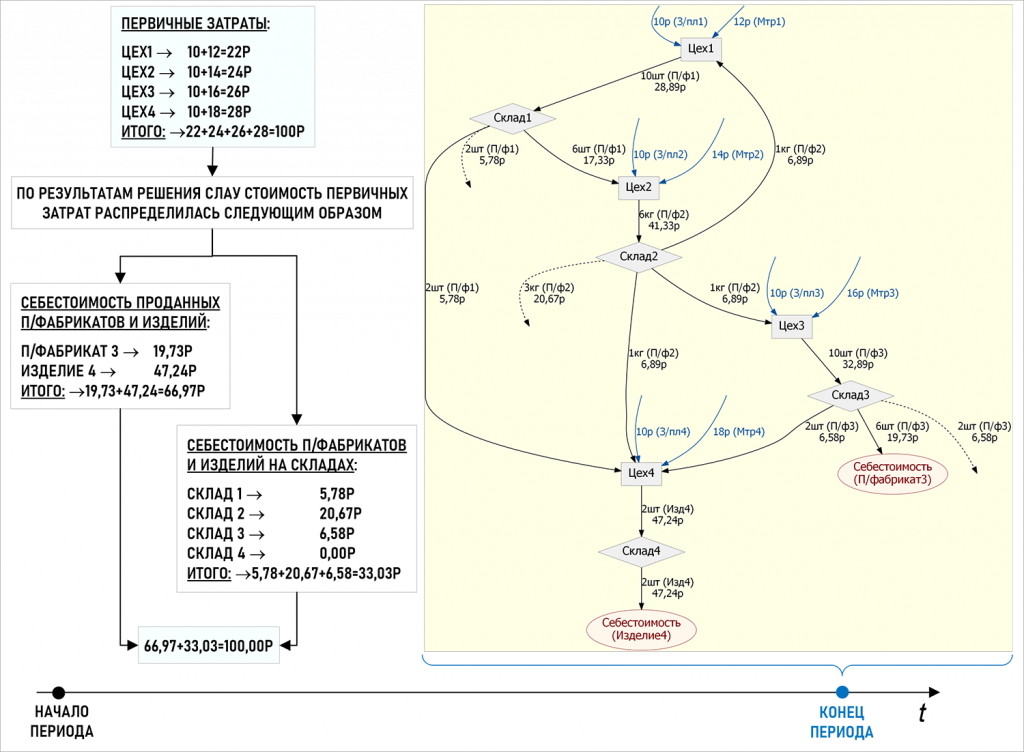
Покажем полученный результат в графическом виде:
На рисунке наглядно виден процесс «взаимодействия» первичных и вторичных затрат. Через центры затрат {Цех1,Цех2,Цех3,Цех4} в Граф затрат поступают (по аналогии с жидкостями – «вливаются») первичные затраты общей стоимостью 100 рублей. Затем эти первичные затраты, но уже в виде вторичных затрат начинают перераспределяться между центрами затрат, финишируя на центрах затрат {Себестоимость(Изделие4),Себестоимость(П/фабрикат3)}, формируя себестоимость проданных изделий и полуфабрикатов. Кстати, именно это в бухгалтерском учете называется расходами экономического субъекта. Часть вторичных затрат не успевает дойти до этих финишных центров затрат и задерживается в центрах затрат {Склад1,Склад2,Склад3} в виде остатков полуфабрикатов.
На этом краткое напоминание об особенностях первичных и вторичных затрат можно закончить и перейти к изучению алгоритма R-S-B.
Алгоритм R-S-B. Cхемы распределения затрат
Напомним, что ключевыми объектами любого Графа затрат являются центры затрат (узлы) и потоки вторичных затрат (дуги), а комбинации этих объектов формируют структуру Графа затрат. И здесь возникает вопрос – а как конкретно происходит формирование этой структуры, на какие алгоритмы можно опираться, например, при написании технического задания на формирование Графа затрат? Можно ли сделать так, чтобы каждый центр затрат «сам понимал» куда ему дальше отправлять поступившие на его вход первичные и вторичные затраты?
Вот именно для этих целей и используются различные СРЗ, в основе которых лежит один и тот же алгоритм R-S-B, получивший свое название в соответствии с названиями трех его этапов выполнения:
- на этапе R (recipient) для центра затрат определяются все его соседние центры затрат, которым необходимо передать потоки вторичных затрат. Это называется подмножеством соседей-получателей затрат
- на этапе S (share) определяется, какая доля от стоимости затрат, накопленных в центре затрат, должна быть передана подмножеству соседей-получателей затрат
- на этапе B (base) определяются значения исходных коэффициентов распределения затрат, в соответствии с которыми стоимость вторичных затрат на выходе центра затрат будет распределена между центрами затрат из подмножества соседей-получателей затрат. Иногда это называют базой распределения
Рассмотрим пример простой СРЗ, использующей алгоритм R-S-B. Выделим в рассмотренном выше Графе затрат центр затрат Склад2, который используется для накопления и распределения вторичных затрат, связанных с движением полуфабриката П/ф2, произведенного Цехом2 в течение рассматриваемого периода.
На этапе R происходит поиск подмножества соседей-получателей затрат {Цех1,Цех3,Цех4,Склад2}, для чего в автоматизированной системе производится анализ всех документов, связанных с движением П/ф2. Поскольку на конец периода есть остаток полуфабриката на складе, то формально считается, что Склад2 выступает как источником, так и получателем вторичных затрат.
На этапе S определяется, что все 100% стоимости вторичных затрат должны быть распределены между центрами затрат из подмножества соседей-получателей затрат.
На этапе B определяется, что стоимости вторичных затрат будут распределяться между соседями-получателями затрат пропорционально движению единиц калькуляции – в данном случае килограммов П/ф2. Выше на рисунке выделены результаты работы алгоритма для Склад2, где остаток П/ф2 показан на главной диагонали на пересечении столбца и строки для Склад2.
СРЗ с таким вариантом работы алгоритма R-S-B можно назвать, например, движение полуфабрикатов и готовой продукции СРЗ=ДвижениеПФиГП. При написании технического задания можно выделить все подобные центры затрат в один класс и присвоить им в качестве общего свойства эту СРЗ. Результатом работы алгоритма R-S-B в любой СРЗ является заполнение ячеек матрицы исходных коэффициентов, то есть данная матрица формируется с помощью именно этого алгоритма.
Выводы
Так или иначе в бухгалтерской литературе и литературе по управленческому учету есть описания фрагментов работы алгоритма R-S-B. Для этого используются такие термины как, например, драйверы затрат, базы распределения затрат, пулы затрат и т.п. Однако найти целостное описание работы этого алгоритма довольно затруднительно. В теории графов затрат ситуация выглядит следующим образом.
Для расчета себестоимости необходимо сформировать структуру Графа затрат, то есть определить множество центров затрат и соединить их между собой потоками вторичных затрат (дугами). Для этого нужно найти все потоки вторичных затрат на выходе каждого центра затрат. Этого будет достаточно, поскольку исходящие потоки вторичных затрат для одного центра затрат будут входящими потоками вторичных затрат для других центров затрат, что в итоге полностью сформирует структуру Графа затрат.
Чтобы сформировать множество дуг на выходе центра затрат для него (или класса центров затрат) задается особое свойство – соответствующая СРЗ на основе алгоритма R-S-B. Например, это могут быть СРЗ=ПропорцЗарПл для центров затрат класса Офис, СРЗ=ВыпускПФиГП для класса производственных центров затрат и т.п., смысл этих СРЗ понятен из их названий. Также необходимо помнить, что в техническом задании на формирование Графа затрат необходимо отразить все три этапа работы алгоритма R-S-B для этих СРЗ. После выполнения СРЗ для каждого центра затрат структура Графа затрат для расчета себестоимости будет полностью сформирована.
Вступайте в нашу телеграмм-группу Инфостарт