Взаиморасчёты.
Тема поднята и рассматривалась samashkov в следующих ссылках:
Тема раскрыта и теоретически и практически Арчибальд
1. //infostart.ru/public/85911/ - обработка
2. //infostart.ru/public/85804/ - статья
Особо остановлюсь на том, что такие задачи были всегДА ... причЁм "сегодня" это задачи олимпиад старшеклассников и прАктика студентов а "вчера" в СССР, будучи студентами, мы подобные задачи описывали на "фортранах" ...
Рассматривая данную задачу, и пробуя её решить, выявил для себя несколько подобных задач, ранее мне уже встречавшихся.
Первая.
На одной из олимпиад по программированию среди школьников, был у меня период преподавания, была задача найти в маршруте автобуса количество левых и правых поворотов. Маршрут автобуса задавался точками. Точки обозначались координатами осей.
Вторая.
Изучая математические методы решения логистических задач, вспомнил о решениях поиска выхода из лабиринта. Лабиринт задавался точками, именнованными буквами.
Третья.
Где-то встречал решение нахождения геометрических фигур внутри других фигур. Например, у вас есть квадрат, пятиугольник и т.д. с проведёнными через вершины отрезками (и любые другие свободные фигуры). Нужно было найти количество всех отрезков, треугольников, четырехугольников и т.д.
И первая, и вторая, и третья задачи схожи. Общий поиск решения заключается в нахождении векторов с одинаковым набором условий на его концах.
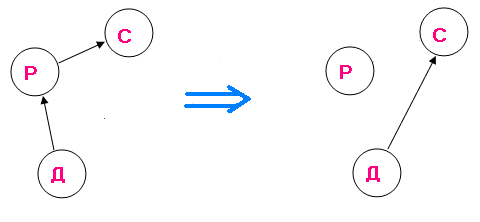
Например, «АВ», «ВС», «СД». У трёх векторов две общие точки. Назовём эту последовательность цепочкой. А называется такая последовательность тупиком.
Если добавить ещё один вектор «ДА», то получим замкнутый контур. Такую последовательность векторов будем назвать замкнутой, или кругом.
Теперь перейдём к нашей задаче и её возможному решению.
Определим «Взаиморасчёт» как операцию списания долгов на сумму долга или его части между двумя и (или) более объектами. Причём у всех участников взаимных зачётов снижается сумма обязательств.
Рассмотрим гипотетическую ситуацию.
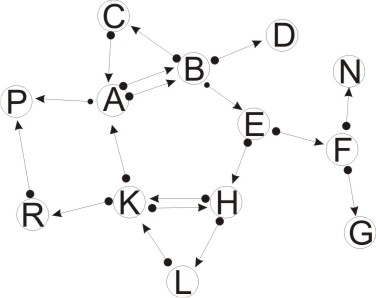
Существует несколько объектов A, B, C, D, E, F, N, G, H, L, K, P, R – 13 участников, образующих между собой поле отношений в виде 18 долгов. Долги как связи обозначаем векторами. Начало, точка вектора, обозначает должника, стрелка - кредитора.
Наша задача - определить количество возможных взаиморасчётов. Для простоты определимся, что первыми закрываются круги обязательств с наименьшим количеством участников, и суммы долгов будем считать равными.
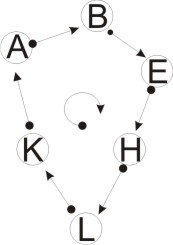
Представим схематично, векторами, состояние связей между объектами:
Вся картинка при рассмотрении в призме нашей задачи раскладывается на несколько схем. Разложим её и каждой части дадим определение и возможность взаимозачёта.
Схема первая. «Тупик». Взаимозачёт невозможен.
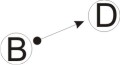
Схема вторая. «Сложный тупик». Сложный тупик разбивается на несколько простых.
Схема третья. «Замкнутый тупик». Замкнутый тупик разбивается на несколько сложных, а затем и на простые.
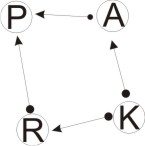
Схема четвёртая. «Круг». Взаимозачёт возможен.
![]()
Схема пятая. «Сложный круг» из 3 векторов. Круг против часовой стрелки.
Схема шестая. «Сложный круг» из 3 векторов. Круг по часовой стрелке.
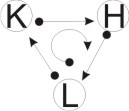
Схема седьмая. «Сложный круг» из 5 векторов. Круг по часовой стрелке.
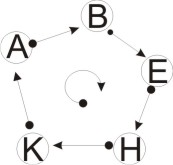
Схема восьмая. «Сложный круг» из 6 векторов. Круг по часовой стрелке.
Теперь в таблицу поместим, в любом порядке, наши вектора взаимных обязательств. У меня это выглядит так.
|
AB |
BD |
BC |
CA |
BE |
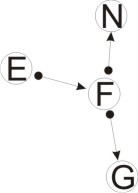
EF |
FN |
FG |
EH |
HL |
LK |
HK |
KH |
KR |
RP |
KA |
AP |
AB |
Решение задачи будет заключаться, в моём варианте, это убрать «тупики», и определить зачёты по восходящим по количеству «кругам».
Сортируем. Получаем следующую картину.
|
AB |
AB |
AP |
BC |
BD |
BE |
CA |
EF |
EH |
FG |
FN |
HK |
HL |
KA |
KH |
KR |
LK |
RP |
Векторы, помеченные синим фоном, являются тупиками. Между ними взаимозачёт невозможен. Убираем их.
Векторы, помеченные зелёным фоном, образуют «круг», и между ними производится простой взаимозачёт. В таблице эти векторы обнуляются.
Наша таблица с векторами, между которыми возможны сложные взаимозачёты, примет следующий вид.
|
AB |
AB |
|
BC |
|
BE |
CA |
|
EH |
|
|
|
HL |
KA |
|
|
LK |
|
А наша схема обязательств будет выглядеть так.
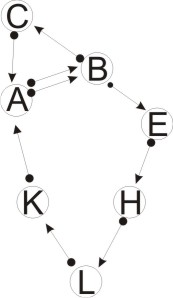
Получаем два круга. Производим взаимозачёты в этих кругах.
Остаточная таблица и схема должников будет выглядеть так.
|
|
|
AP |
|
BD |
|
|
EF |
|
FG |
FN |
|
|
|
|
KR |
|
RP |
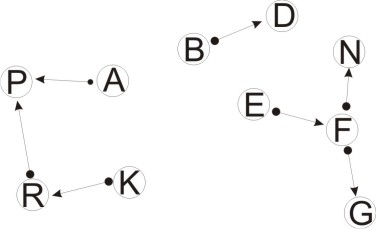
Из 18 долгов осталось между 13 участниками осталось 7 долгов и 10 участников.
В файле лежит обработка в виде примера решения данной задачи для 1С 7. Даем обработке наши долги в виде 18 векторов, получаем на выходе таблицы «тупики» и «зачёты».
Не претендую на полноту описания и решения задачи.
Буду благодарен за комментарии, суровую критику и добрые пожелания.
С уважением Шёпот теней, в миру Александр Шишкин.
Вступайте в нашу телеграмм-группу Инфостарт