Чем хороша математика? Возможно, тем, что с помощью универсального языка формулирует методы и решения, которые впоследствии можно применять к самым разным явлениям окружающего мира. Задача разработчика состоит в том, чтобы за различными формами разглядеть общее содержание и эффективно использовать разработанный для этого содержания математический аппарат. Проиллюстрируем данный тезис с помощью статей, которые были в разное время размещены на портале infostart.
Начнем с "ФИФО для любопытных". В данной публикации обсуждается, как одним запросом получить все движения расходных документов за период. Есть таблица приходных накладных, которые формируют партии товаров, и таблица расходных накладных, в которых эти товары списываются. Необходимо для каждого документа списания указать документы партии и количество товара, которое списывается с каждой партии. Теперь обратимся к "Распределение в запросе" или "избавляемся от перебора". Автор приводит найденное им решение для следующей задачи. Есть складские ячейки с известной емкостью (A, B, C, D) и сам товар (X, Y, Z), который необходимо «как-то» разложить по этим ячейкам, но так, чтоб в ячейку не положили больше товара, чем может быть в ней места.
При всей ,на первый взгляд,непохожести обсуждаемых в данных статьях темах речь идет об одной и той же математической задаче. Есть два множества отрезков. Отрезки заданы координатами начала и конца, причем координаты правой точки больше координаты левой. Каждому отрезку сопоставлен уникальный индекс,например ссылка на документ. Надо определить какие отрезки пересекаются и вычислить длину этого пересечения. Покажем как формируются эти отрезки. Рассмотрим задачу "Ячейки и Товары".
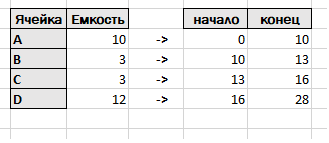
Таблица с ячейками переходит в таблицу с отрезками, где начало и конец определяются с помощью запроса с нарастающими итогами. Аналогично строим таблицу для товаров.
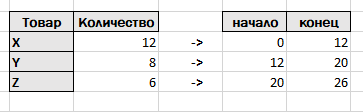
Понятно, что если поменять местами строчки в каждой таблице, то поменяются значения в колонках начало и конец. На числовой прямой отрезки будут выглядеть следующим образом.
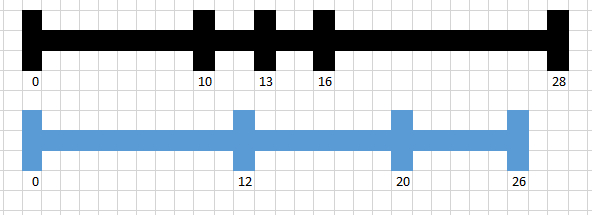
Найдем критерий, по которому мы можем собрать пересекающиеся отрезки. Эта задача решена древними греками, а может и еще раньше. Приведем одно из возможных рассуждений. Даны два отрезка А(начало,конец) и Б(начало,конец). Начало и конец это координаты отрезка. Проще всего сформулировать правило , при котором отрезки НЕ пересекаются. Оно такое (А.конец < Б.начало ИЛИ A.начало>Б.конец). Применим к данному выражению отрицание, тогда оно трансформируется в условие (А.конец>= Б.начало И A.начало<=Б.конец). После этого становится понятно, как выбрать все пары пересекающихся отрезков.
Текст="ВЫБРАТЬ
| А.индекс КАК Аи,
| Б.индекс КАК Би
|ИЗ
| А КАК А
| ВНУТРЕННЕЕ СОЕДИНЕНИЕ Б КАК Б
| ПО А.конец >= Б.начало
| И А.начало <= Б.конец";
Теперь осталось добавить длину пересечения. А она равна Мин(А.конец,Б.конец)-Макс(А.начало,Б.начало), что на языке запросов выглядит как:
Текст="ВЫБРАТЬ
| А.индекс КАК Аи,
| Б.индекс КАК Би,
| ВЫБОР
| КОГДА А.конец < Б.конец
| ТОГДА А.конец
| ИНАЧЕ Б.конец
| КОНЕЦ - ВЫБОР
| КОГДА А.начало > Б.начало
| ТОГДА А.начало
| ИНАЧЕ Б.начало
| КОНЕЦ КАК Пересечение
|ИЗ
| А КАК А
| ВНУТРЕННЕЕ СОЕДИНЕНИЕ Б КАК Б
| ПО А.конец >= Б.начало
| И А.начало <= Б.конец";
Применим предложенный алгоритм к нашим данным.
Функция ДобавитьОтрезок(длина,куда)
запись =куда.Добавить() ;
запись.индекс =куда.Количество();
если запись.индекс=1 тогда
запись.начало =0 ;
иначе
запись.начало =куда[запись.индекс-2].конец;
конецесли;
запись.конец =запись.начало+длина;
возврат запись;
КонецФункции
Функция Пересечение() export
start=ТекущаяУниверсальнаяДатаВМиллисекундах();
типЧ=новый ОписаниеТипов("Число");
тзА = new ТаблицаЗначений;
тзА.Колонки.Добавить("индекс",типЧ);
тзА.Колонки.Добавить("начало",типЧ);
тзА.Колонки.Добавить("конец",типЧ);
ДобавитьОтрезок(10,тзА);
ДобавитьОтрезок(3 ,тзА);
ДобавитьОтрезок(3 ,тзА);
ДобавитьОтрезок(13,тзА);
тзБ = тзА.СкопироватьКолонки();
ДобавитьОтрезок(12,тзБ);
ДобавитьОтрезок(8 ,тзБ);
ДобавитьОтрезок(6 ,тзБ);
Текст="ВЫБРАТЬ
| тз.индекс КАК индекс,
| тз.начало КАК начало,
| тз.конец КАК конец
|ПОМЕСТИТЬ А
|ИЗ
| &тзА КАК тз
|;
|
|////////////////////////////////////////////////////////////////////////////////
|ВЫБРАТЬ
| тз.индекс КАК индекс,
| тз.начало КАК начало,
| тз.конец КАК конец
|ПОМЕСТИТЬ Б
|ИЗ
| &тзБ КАК тз
|;
|
|////////////////////////////////////////////////////////////////////////////////
|ВЫБРАТЬ
| А.индекс КАК Аи,
| Б.индекс КАК Би,
| ВЫБОР
| КОГДА А.конец < Б.конец
| ТОГДА А.конец
| ИНАЧЕ Б.конец
| КОНЕЦ - ВЫБОР
| КОГДА А.начало > Б.начало
| ТОГДА А.начало
| ИНАЧЕ Б.начало
| КОНЕЦ КАК Пересечение
|ИЗ
| А КАК А
| ВНУТРЕННЕЕ СОЕДИНЕНИЕ Б КАК Б
| ПО А.конец >= Б.начало
| И А.начало <= Б.конец";
запрос=новый запрос(Текст);
запрос.Параметры.Вставить("тзА",тзА);
запрос.Параметры.Вставить("тзБ",тзБ);
ответ=запрос.Выполнить().Выгрузить();
end=ТекущаяУниверсальнаяДатаВМиллисекундах();
message("выполнение запроса "+(end-start));
возврат ответ;
КонецФункции
Функция ДобавитьОтрезок добавляет отрезок в массив, функция Пересечение возвращает пересечение отрезков из приведенного выше примера.
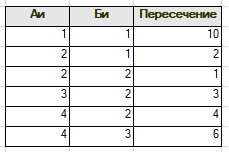
Именно этот алгоритм и реализован в приведенных выше публикациях. Можно ли предложить более эффективное решение. Да, можно, и вот почему. Приведенный запрос будет правильно работать для любых наборов отрезков, в том числе и пересекающихся внутри одного множества. В тоже время, по условиям задачи отрезки расположены непрерывно на числовой прямой,не пересекаются и конец предыдущего совпадает с началом следующего (спасибо нарастающим итогам).
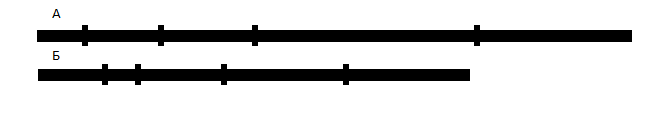
В этом случае мы можем заменить представление отрезка его длиной и порядком следования(индексом) А[индекс](длина). Индекс - это номер отрезка в таблице, длина - колонка из таблицы, в которой хранятся рассматриваемые отрезки. Рассмотрим два левых отрезка А и Б. Они пересекаются и длина пересечения равна длине минимального из них. Уберем этот отрезок из множества, в которое он входит, а второй укоротим на длину пересечения. Повторим нашу процедуру. Остановимся, когда обработаем все отрезки в первом или втором множестве. Именно такой алгоритм предложил Сергей в публикации "Минимализмы" раздел 7. Связывание таблиц значений по ФИФО. Кстати, частным случаем данного алгоритма является списание по партии внутри одного расходного документа, что вполне естественно. Предложенный алгоритм показывает значительный выигрыш в быстродействии по сравнению с запросом, поскольку учитывает особенность расположения отрезков в исходных множествах.
Надеюсь, что данная статья будет полезна при поиске общих математических подходов для непохожих, в первом приближении, процессов.
Вступайте в нашу телеграмм-группу Инфостарт