Генератор псевдослучайных чисел
Введение в проблему
Проблема случайных чисел начинается с того, что пока не существует ни одного генератора случайных чисел. Быть может, некоторые читатели возразят, и будут настаивать на том, что непосредственно человек является генератором случайных чисел. Но, к сожалению, это не так. Если попросить респондента загадать случайное число, то с высокой долей вероятности это будет число из промежутка от 0 до 20. Из этого интервала, скорее всего, будет загадано число «3», «7», «10», «12». Если же «случайное» число не будет принадлежать данному отрезку, то оно будет либо из повторяющихся цифр, например «111», «666» и так далее, либо будет кратно 10 («100», «1000»). Еще респонденты называют какие-то культовые числа, как то «42», «23», «13».
Таким образом, даже человек является своего рода генератором псевдослучайных чисел, и «программа», заложенная в нём – еще проще и более предсказуемо, чем машинная.
Тема создания качественного генератора псевдослучайных чисел не теряет своей актуальности и по сей день, так как псевдослучайные числа находят широчайшее применение в программировании, при создании игр с открытым миром, при розыгрышах призов, при создании прогнозов погоды, а также при моделировании сложных систем частиц (пылевое облако, имитация огня).
Кроме всего вышеперечисленного (данные вещи имеют явный развлекательный характер), псевдослучайные числа также применяются в криптографии, современном шифровании, создании «одноразовых» паролей, при передаче информации между пользователями.
В обозримом будущем при сохранении современных тенденций на развитие искусственного интеллекта, можно с твердой уверенностью говорить о переходе от генераторов псевдослучайных чисел к случайным, или, по крайней мере, псевдослучайные алгоритмы будут не такими предсказуемыми.
Способы решения
Генератор псевдослучайных чисел с равномерным распределением
Встроенный в Pascal генератор случайных чисел является эталоном для наших последующих экспериментов. Данное изображение было создано при использовании графических средств. Были созданы 5000 случайных чисел для x, 5000 – для y, а после по полученным значениям были построены точки с координатами (x, y).
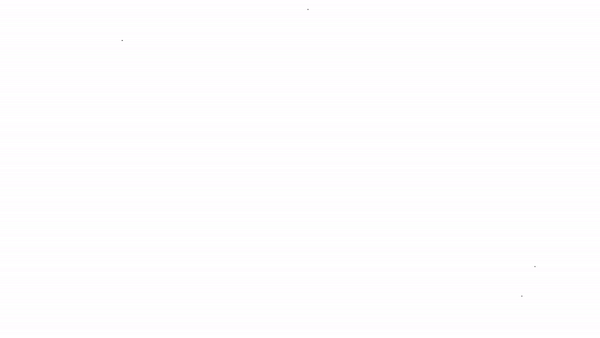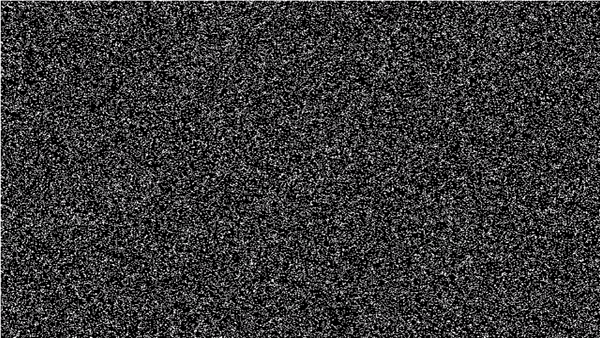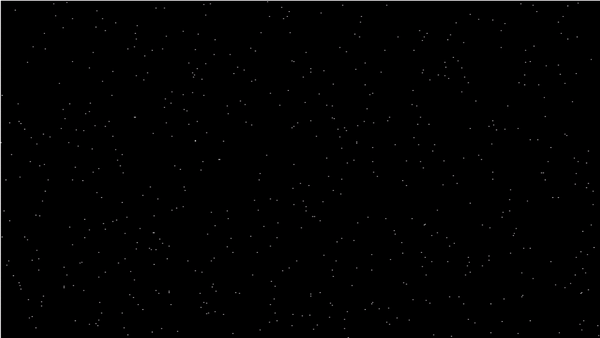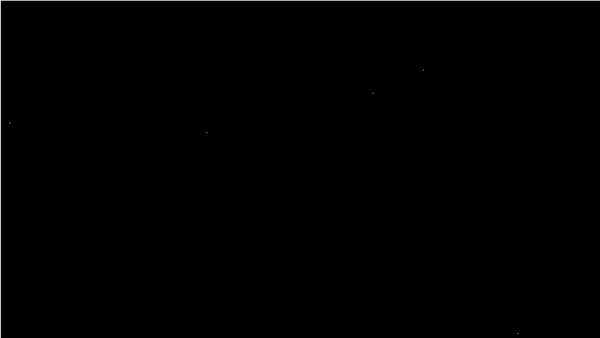
Это похоже на равномерное распределение.
Возникла идея проанализировать распределение у цифр десятичной записи деления единицы на большое простое число.
Была создана простая программа в Pascal:
program pseudorandomnumbersgeneratorthree;
begin
writeln(1/9941);
end.
В результате: 0.000100593501659793
Очевидно, что для нашего эксперимента такой точности недостаточно. Самый большой тип данных в Pascal – real (действительные числа) – ограничен 1.7*10^38, поэтому возникла идея обратиться к Java.
«Я же просил 400 капель, а тут 402!»

Будем запрашивать текущее время в миллисекундах, проверять, является ли оно простым числом (если нет, то будем увеличивать его на 1 до тех пор, пока оно не станет простым), а дальше – находить величину, обратную ему и брать значения с 1 цифры, не равной 0, по 1001 цифру после запятой.
import java.math.BigDecimal;
import java.math.BigInteger;
public class testing {
public static void main(String[] args) {
BigDecimal input = BigDecimal.valueOf(1.0);
BigInteger helper = BigInteger.valueOf(1);
BigInteger input1 = BigInteger.valueOf((int)System.currentTimeMillis());
boolean primenumber = input1.isProbablePrime(100);
while (primenumber != true) {
input1 = input1.add(helper);
primenumber = input1.isProbablePrime(100);
}
if (primenumber) {
BigDecimal input3 = new BigDecimal(input1.toString());
BigDecimal input4 = input.divide(input3, 1001, BigDecimal.ROUND_DOWN);
System.out.println(input4);
}
}
}
Код реализации представлен выше.
4.7538831794067873244780700842245055046014363666920473795748060044741066957557031955004218080137080617
43531713352213668782593606537595673675749399898191883684123712152189036251666519504666651086923785569
44946106550351530716892661986597665237619116547410840382592955635910749298428932360835951664830022123
52170877653930812222851849223500269856793314774956207026111269550378446728066145275750127622628987275
12734325515752933896916389254566430553665088075262596175650159021409382443634739080628286530878836069
43467957883962681300156073264959318618545868930733448630624863330909592932984132787743028009955279807
34348374324813756512560274918623538777356400809221777690778968906574356929374952351531775107057722548
52366643751729578576570687269086156049599178074895677210214004955344191560324039072266633867788443776
53695732699630183590304829291128412977753665997778347807458472571144900699645008099611491416721065391
50431169574389692662436505169336677468936015393153600156591390687042164296363795591E-10
Подсчитаем, сколько раз встречается та или иная цифра («отбросим» нули после запятой до первой цифры, не равной «0», отбросим последнюю, 1001 цифру последовательности (округление)):
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
97 |
84 |
88 |
105 |
83 |
115 |
125 |
106 |
86 |
101 |
Получилось распределение — последовательность цифр [0-9], близкое к равномерному. Величина выборки 1000, повторение цифр из-за периодичности дроби внутри выборки отсутствуют. Поставленная задача достигнута, генератор создан.
Еще один вариант генератора псевдослучайных чисел с равномерным распределением – получать случайное число как результат действий пользователя, проверять простое ли это число. Если да – делить единицу на него, если нет – искать ближайшее простое. Вот код реализации на Java:
package education1;
import java.math.BigDecimal;
import java.math.BigInteger;
import java.util.Scanner;
public class testing {
public static void main(String[] args) {
BigDecimal input = BigDecimal.valueOf(1.0);
BigInteger helper = BigInteger.valueOf(1);
Scanner in = new Scanner(System.in);
System.out.println("Введите число от 0 до 9");
BigInteger input1 = BigInteger.valueOf((int)System.currentTimeMillis());
int onlyforlools = in.nextInt();
System.out.println("Введите число от 0 до 9");
int onlyforlools1 = in.nextInt();
System.out.println("Введите число от 0 до 9");
int onlyforlools2 = in.nextInt();
BigInteger input9 = BigInteger.valueOf((int)System.currentTimeMillis());
BigInteger firstcontrolnumber = input9.subtract(input1);
boolean primenumber = input9.isProbablePrime(100);
while (primenumber != true) {
input9 = input9.add(helper);
primenumber = input9.isProbablePrime(200);
}
if (primenumber) {
BigDecimal input11 = new BigDecimal(input9.toString());
BigDecimal input12 = input.divide(input11, 1001, BigDecimal.ROUND_DOWN);
System.out.println(input12);
}
}
}
Каждое рациональное число представимо в виде бесконечной периодической дроби. Ниже вспомогательная программа, которая ищет длину возможного периода для бесконечной дроби и показывает распределение цифр 0-9.
import java.math.BigInteger;
public class testing {
public static void main (String [] args) {
BigInteger ten = new BigInteger("10");
BigInteger helper = BigInteger.valueOf(9947); /*здесь вводите число, далее Java преобразует его в бесконечную десятичную периодическую дробь вида 1/число, а потом – находит количество чисел в периоде*/
BigInteger lools = new BigInteger("1");
boolean primenumber = helper.isProbablePrime(100);
while (primenumber != true) {
helper = helper.add(lools);
primenumber = helper.isProbablePrime(100);
}
BigInteger three = helper;
BigInteger end123 = new BigInteger ("1");
String period = "";
do {
end123 = end123.multiply(ten);
period = period + end123.divide(three).toString();
end123 = end123.mod(three);
}
while (end123.compareTo(lools) != 0);
int resultat = period.length();
int[][]amountofnumbers = {{0, 0}, {1, 0}, {2, 0}, {3,0}, {4, 0}, {5,0}, {6, 0}, {7,0}, {8,0}, {9,0}};
for (char element: period.toCharArray()) {
if (element == '0') amountofnumbers[0][1] = amountofnumbers[0][1] + 1;
if (element == '1') amountofnumbers[1][1] = amountofnumbers[1][1] + 1;
if (element == '2') amountofnumbers[2][1] = amountofnumbers[2][1] + 1;
if (element == '3') amountofnumbers[3][1] = amountofnumbers[3][1] + 1;
if (element == '4') amountofnumbers[4][1] = amountofnumbers[4][1] + 1;
if (element == '5') amountofnumbers[5][1] = amountofnumbers[5][1] + 1;
if (element == '6') amountofnumbers[6][1] = amountofnumbers[6][1] + 1;
if (element == '7') amountofnumbers[7][1] = amountofnumbers[7][1] + 1;
if (element == '8') amountofnumbers[8][1] = amountofnumbers[8][1] + 1;
if (element == '9') amountofnumbers[9][1] = amountofnumbers[9][1] + 1;
}
System.out.println(resultat);
System.out.println(period);
for (int i = 0; i < amountofnumbers.length; i++) {
for (int j = 0; j < amountofnumbers[i].length; j++) {
System.out.print(amountofnumbers[i][j] + "\t");
}
System.out.println();
}
}
}
Чем больше простое число, тем больше получившийся период. Например, для числа 3 – в периоде всего одно число, для числа 101 – 4 числа, для 7369 – 1842 числа.
Генератор псевдослучайных чисел с нормальным распределением
Кроме генераторов с равномерным распределением также существуют генераторы с нормальным распределением (имеющим большое значение в физике, биологии, социологии). Воспользуемся центральной предельной теоремой (Сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.) ссылка: https://ru.wikipedia.org/wiki/Центральная_предельная_теорема для небольшого видоизменения лучшей программы по генерации псевдослучайной последовательности с равномерным распределением, чтобы получить последовательность случайных чисел с нормальным распределением.
Код представлен ниже:
import java.math.BigDecimal;
import java.math.BigInteger;
public class testing {
public static void main(String[] args) {
BigDecimal input = BigDecimal.valueOf(1.0);
BigInteger helper = BigInteger.valueOf(1);
BigDecimal divider = new BigDecimal("100.0");
BigInteger input1 = BigInteger.valueOf((int)System.currentTimeMillis());
BigDecimal summary = new BigDecimal("0");
int counter;
boolean primenumber = input1.isProbablePrime(100);
if (primenumber == true) {
counter = 1;
}
else {
counter = 0;
}
while (counter < 101) {
while (primenumber != true) {
input1 = input1.add(helper);
primenumber = input1.isProbablePrime(200);
}
if (primenumber) {
BigDecimal input3 = new BigDecimal(input1.toString());
BigDecimal input4 = input.divide(input3, 1001, BigDecimal.ROUND_DOWN);
summary = summary.add(input4);
}
counter = counter + 1;
primenumber = false;
}
System.out.println(summary.divide(divider, 1001, BigDecimal.ROUND_DOWN));
}
}
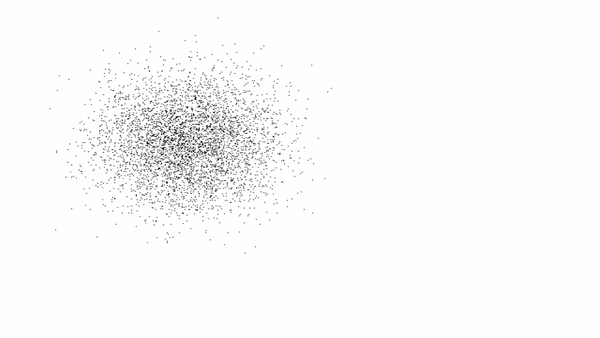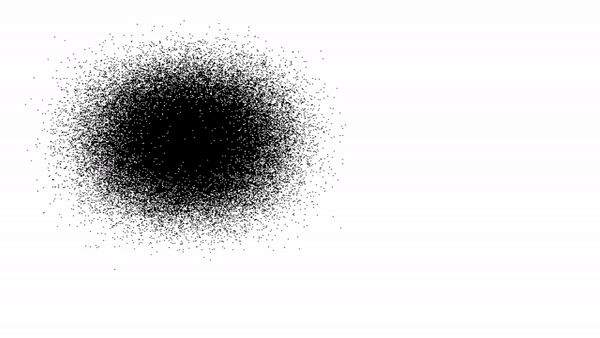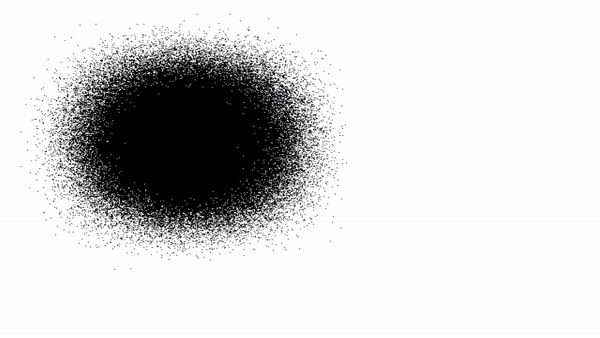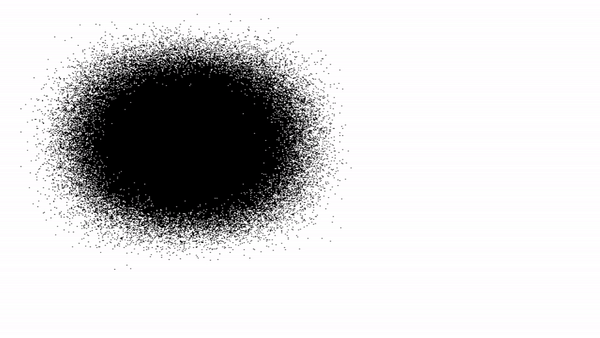
Нормальное распределение, изображенное с помощью графических ресурсов Pascal
Генератор псевдослучайных чисел с логнормальным распределением

Логнормальное распределение, изображенное с помощью графических ресурсов Pascal
Белые полосы наблюдаются из-за округления значения функции e^(случайное число с нормальным распределением)
В жизни логнормальное распределение имеет размер заработной платы, сумма чеков и другие случайные величины. Код, позволяющий получить псевдослучайную величину с логнормальным распределением представлен:
import java.math.BigDecimal;
import java.math.BigInteger;
import org.nevec.rjm.*;
public class testing {
public static void main(String[] args) {
BigDecimal input = BigDecimal.valueOf(1.0);
BigInteger helper = BigInteger.valueOf(1);
BigInteger input1 = BigInteger.valueOf((int)System.currentTimeMillis());
BigDecimal summary = new BigDecimal("0");
BigDecimal divider = new BigDecimal("100.0");
BigDecimal eulerdigit = new BigDecimal("2.7182818284590455");
int counter;
boolean primenumber = input1.isProbablePrime(100);
if (primenumber == true) {
counter = 1;
}
else {
counter = 0;
}
while (counter < 101) {
while (primenumber != true) {
input1 = input1.add(helper);
primenumber = input1.isProbablePrime(200);
}
if (primenumber) {
BigDecimal input3 = new BigDecimal(input1.toString());
BigDecimal input4 = input.divide(input3, 1001, BigDecimal.ROUND_DOWN);
summary = summary.add(input4);
}
counter = counter + 1;
primenumber = false;
}
System.out.println(eulerdigit.pow(summary.divide(divider, 1001, BigDecimal.ROUND_DOWN)).toString());
}
}
Итог
В данной статье представлены рабочие алгоритмы разных распределений для создания последовательности псевдослучайных цифр. Надеюсь, эта статья была интересной для вас!
Автор: Васильев Алексей. Консультант-математик: Васильев Николай.
Вступайте в нашу телеграмм-группу Инфостарт