В предыдущей статье Балансовые уравнения в Графе затрат на конкретном примере была рассмотрена процедура составления СЛАУ – системы линейных алгебраических уравнений, каждое из которых представляет собой уравнение баланса затрат для соответствующего счета учета в границах Графа затрат. Данная СЛАУ представляет собой математическую модель для расчета себестоимости на Графе затрат и в принципе на этом можно было бы и завершить обсуждение темы расчета себестоимости продукции, поскольку далее нужно просто выполнить ряд очевидных операций чисто технического характера – решить данную СЛАУ каким-либо прямым или итерационным методом и получить значения тарифов.
Подобные алгебраические задачи решаются уже не одно столетие, а в связи с развитием информационных технологий за последние несколько десятилетий было придумано еще и большое количество различных численных методов решения СЛАУ. Поэтому обсуждать в данной статье «технику» решения СЛАУ, особенно в контексте каких-то «новых» технологий бухгалтерского учета, было бы несколько неуместно, т.к. подобные вопросы решаются не методологами учета, а прикладными математиками, специализирующимися на создании и применении численных методов. Проще говоря, если задачу расчета себестоимости удалось свести к решению СЛАУ, составленной для Графа затрат, то все последующие действия по решению СЛАУ становятся очевидными. Решив СЛАУ, мы найдем значения тарифов. Умножив полученные тарифы на известные количества продукции и услуг, определим суммы всех хозяйственных операций, т.е. найдем стоимости вторичных затрат. Вот, собственно, и все, что нужно сделать для расчета себестоимости в нашем примере.
Так что же тогда имеет смысл обсудить в данной ситуации с точки зрения специалиста по расчету себестоимости? Дело в том, что самым интересным в данной задаче является не сам факт решения СЛАУ, такие задачи легко решаются студентами первых-вторых курсов любого технического ВУЗа. Гораздо важнее здесь то, что для расчета себестоимости мы использовали абстрактную бухгалтерскую модель в виде Графа затрат, и поэтому хотелось бы понять, какие «бонусы» может из этого извлечь пользователь такой модели? Каким образом можно использовать данную модель на практике и какие дополнительные задачи можно решить с ее помощью? Вот эти вопросы мы и рассмотрим в данной статье.
Первое, что необходимо обсудить, это вопрос удобства работы с системами уравнений баланса затрат, составленными для Графа затрат. Ведь очевидно, что в практической работе использовать СЛАУ в том виде, в каком они были записаны для нашего примера в предыдущей статье, не очень удобно (мягко говоря). Составить такую СЛАУ один-два раза в учебных целях конечно можно и даже нужно(!). Но выполнять подобные процедуры каждый раз при «закрытии» затрат периода вряд ли кому-то захочется. Кроме того, обсуждение с коллегами каких-либо особенностей записанных таким образом СЛАУ может вообще превратиться в трудно выполнимую задачу из-за большого числа содержащихся в СЛАУ уравнений. Поэтому сначала необходимо найти более удобную для практического применения форму записи СЛАУ для Графа затрат, и такая форма записи существует – это матричная форма записи СЛАУ.
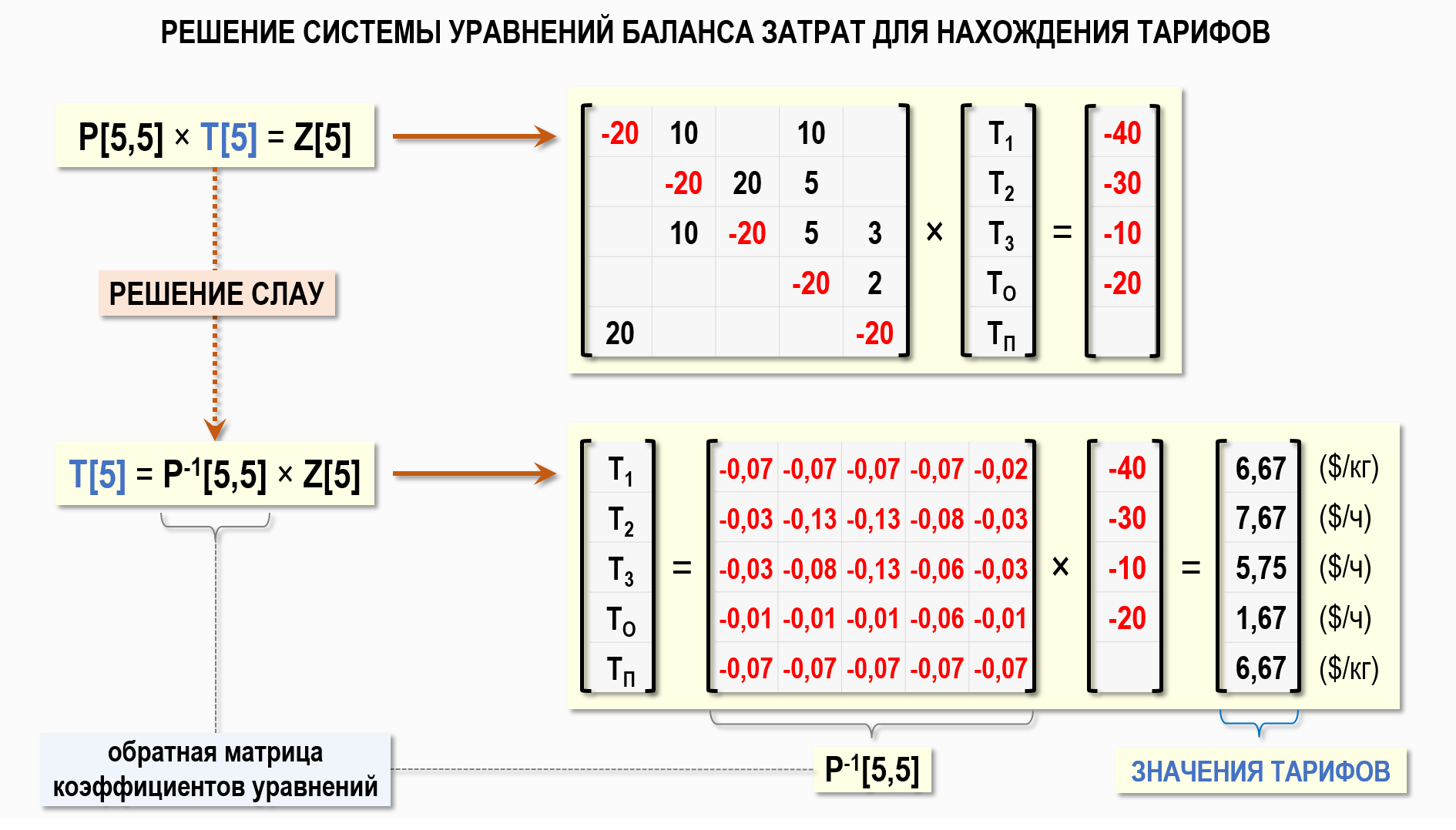
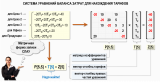
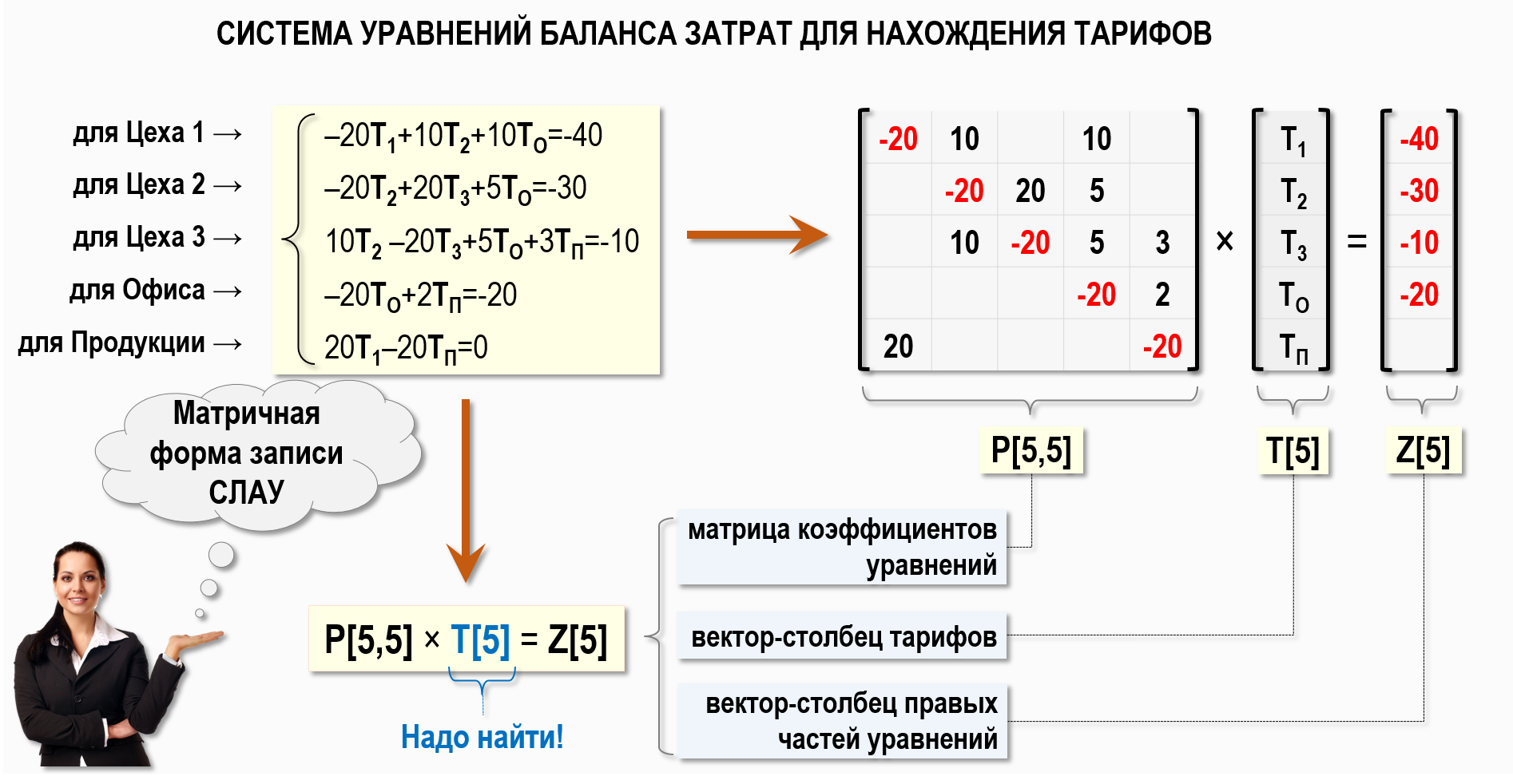
В верхнем левом углу выше на рисунке представлена СЛАУ, которая была составлена в предыдущей статье, только в данном случае был немного изменен порядок расположения неизвестных тарифов в левой части каждого уравнения. Теперь упорядочены не только уравнения в системе, но и неизвестные тарифы, которые должны быть расставлены в каждом уравнении в определенном порядке:
Т1 → Т2 → Т3 → ТО → ТП
Это позволяет записать СЛАУ в следующем виде:
P[5,5]×T[5]=Z[5]
где:
P[5,5] – квадратная матрица коэффициентов уравнений
T[5] – вектор-столбец тарифов
Z[5] – вектор-столбец правых частей уравнений
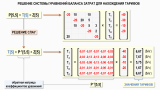
Подобное представление математической модели для расчета себестоимости на Графе затрат гораздо нагляднее и удобнее для практической работы, ведь любая матрица представляет собой таблицу, а с таблицами, в отличие от уравнений, любой учетный специалист работает постоянно. Решение СЛАУ, записанной в матричной форме, можно найти с помощью обратной матрицы коэффициентов уравнений:
В данной статье мы, конечно, не будем обсуждать такие вопросы, как получение обратной матрицы и произведение матриц. Предполагается, что читатель знаком с основами линейной алгебры, поэтому выше на рисунке просто представлена обратная матрица коэффициентов уравнений, которую для нашего примера легко можно получить, например, с помощью формулы МОБР() в Microsoft Excel, а также показан результат решения СЛАУ – вектор-столбец тарифов Т[5], который можно получить с помощью формулы МУМНОЖ() в Microsoft Excel.
В данном же случае важно отметить, что теперь задачу расчета себестоимости на Графе затрат можно представить с помощью матричной формы записи СЛАУ, что позволяет сделать работу с Графом затрат гораздо более технологичной.
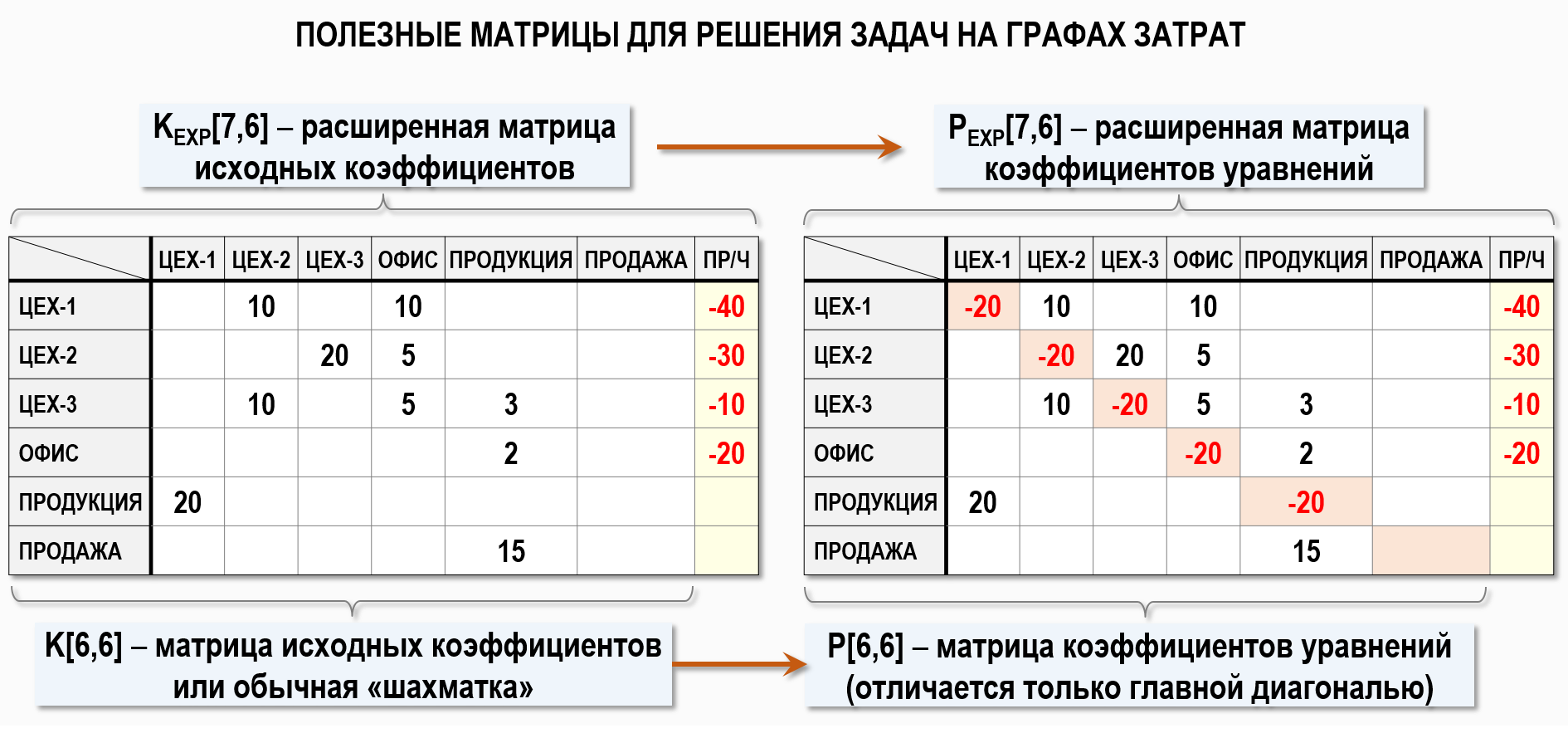
Применение «матричного» подхода к решению задач на Графах затрат не ограничивается использованием только рассмотренных выше видов матриц. Очень полезными для практической работы с Графами затрат является, например, такой класс матриц, как расширенные матрицы исходных коэффициентов. Для нашего примера такая матрица имеет следующий вид:
Расширенная матрица исходных коэффициентов KEXP[7,6] является прямоугольной матрицей из 7-ми столбцов и 6-ти строк и формируется из квадратной матрицы исходных коэффициентов K[6,6] добавлением справа вектора-столбца правых частей уравнений Z[6]. Элементы матрицы K[6,6] называются исходными коэффициентами, их значения определяются количествами единиц калькуляции, которыми обменялись между собой счета учета в Графе затрат, т.е. матрица K[6,6] фактически представляет собой широко известную «шахматку», в столбцах которой находятся источники затрат, а в строках – получатели затрат. Правый столбец матрицы KEXP[7,6] содержит стоимости первичных затрат (со знаком минус), поступивших в дебет счетов учета. В практической работе матрица KEXP[7,6] полезна тем, что в ней в наглядном виде фактически содержится вся информация, необходимая для расчета себестоимости.
Из матрицы KEXP[7,6] легко можно получить расширенную матрицу коэффициентов уравнений PEXP[7,6], которая отличается только значениями элементов на главной диагонали квадратной матрицы коэффициентов уравнений P[6,6], полученными суммированием значений элементов соответствующего столбца (со знаком минус). Расширенная матрица PEXP[7,6] фактически объединяет в себе две матрицы из балансового уравнения для расчета себестоимости, но она менее наглядна из-за наличия элементов на главной диагонали. Поскольку обе расширенные матрицы можно получить друг из друга путем однозначных преобразований, то для практической работы достаточно пользоваться одной из них, и именно расширенная матрица исходных коэффициентов KEXP[7,6] наиболее удобна для этих целей.
Таким образом, для расчета себестоимости на Графе затрат для нашего примера необходимо сделать следующее:
- сформировать «шахматку» – матрицу исходных коэффициентов K[6,6]
- добавить к ней справа столбец, в который нужно записать стоимости первичных затрат со знаком минус – вектор-столбец правых частей уравнений Z[6]
- в результате будет сформирована расширенная матрица исходных коэффициентов KEXP[7,6]
На этом задачу расчета себестоимости можно считать фактически решенной, т.к. далее надо просто преобразовать матрицу KEXP[7,6] в расширенную матрицу коэффициентов уравнений PEXP[7,6], т.е. записать СЛАУ в матричной форме, и решить полученную СЛАУ каким-либо методом – найти значения тарифов.
Безусловно, при использовании матричной формы записи СЛАУ предполагается, что задача расчета себестоимости на Графе затрат будет решаться в автоматизированной системе, т.е. все технические операции по решению СЛАУ будут производится автоматически с помощью математических библиотек численных методов решения СЛАУ. Поэтому специалисту по расчету себестоимости фактически придется иметь дело только с расширенной матрицей исходных коэффициентов KEXP[7,6] – своего рода «интерфейсной» частью данной задачи, работа с которой не представляет особых сложностей и в то же время имеет очевидные преимущества – прозрачность и наглядность представления задачи.
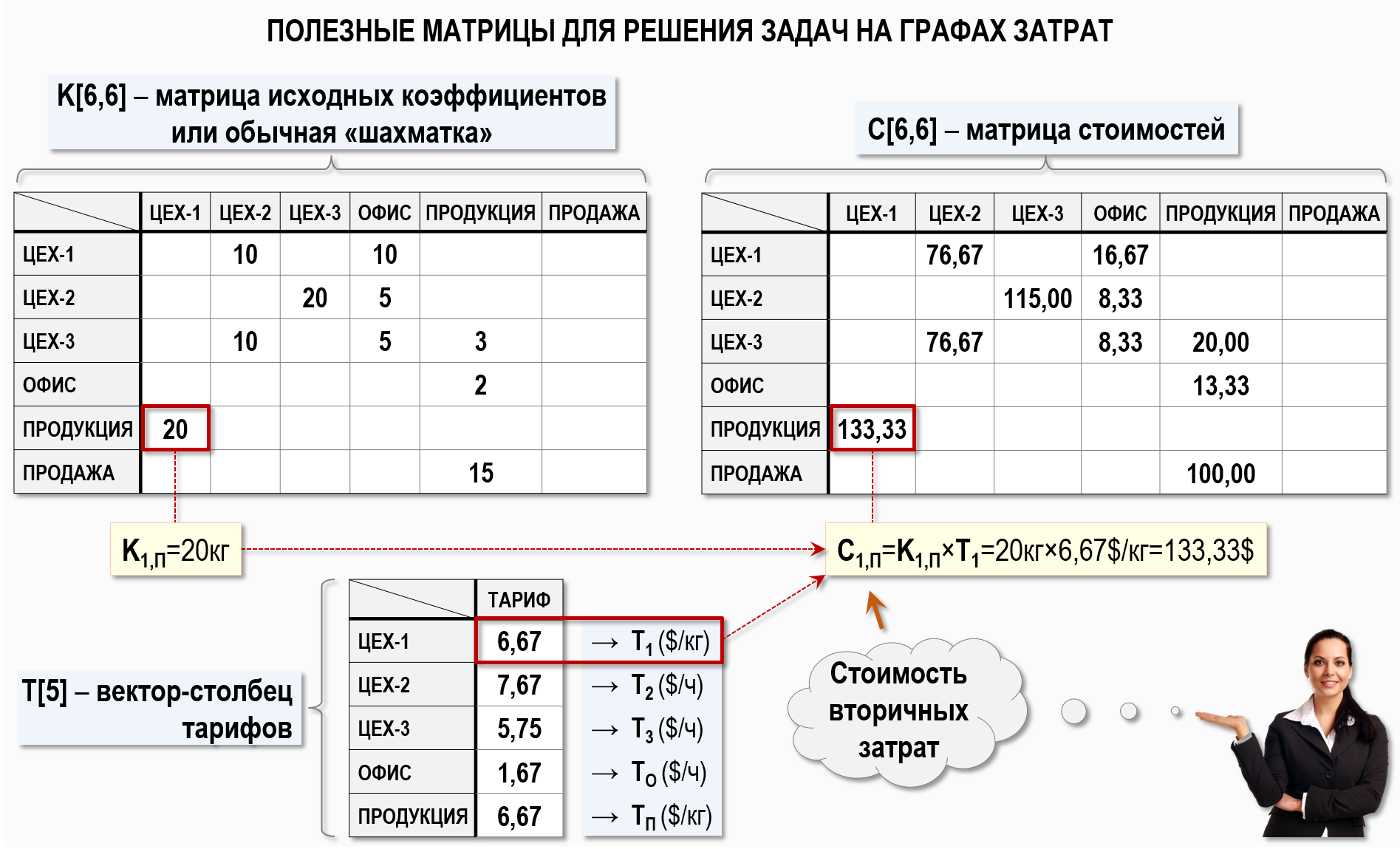
Кроме рассмотренных выше матриц можно также работать и с квадратной матрицей стоимостей C[6,6] – «шахматкой», значения элементов которой определяются уже после проведения процедуры «закрытия» затрат периода как произведения исходных коэффициентов и соответствующих тарифов. Проще говоря, значения элементов данной матрицы представляют собой суммы хозяйственных операций, отраженных в Графе затрат, т.е. представляют собой стоимости вторичных затрат, которые можно далее внести в журнал хозяйственных операций.
Необходимо отметить, что рассмотренные выше матрицы KEXP[7,6] и C[6,6] составлены для всего Графа затрат, т.е. они содержат также столбцы и строки для счета учета «Продажа». Это дает возможность пользователю наглядно увидеть всю абстрактную бухгалтерскую модель для расчета себестоимости. Но из предыдущей статьи мы помним, что для решения СЛАУ в нашем примере не составляется уравнение баланса затрат для счета учета «Продажа», поскольку тариф для этого счета учета определять не нужно. Поэтому в процессе решения СЛАУ необходимо будет преобразовать матрицу PEXP[7,6], убрав из нее столбец и строку для счета учета «Продажа». Как решаются подобные задачи можно посмотреть, например, в статье Расчет себестоимости (СЛАУ). Пример, в которой подробно показаны все этапы преобразования матриц и решен пример в Microsoft Excel.
ВЫВОДЫ:
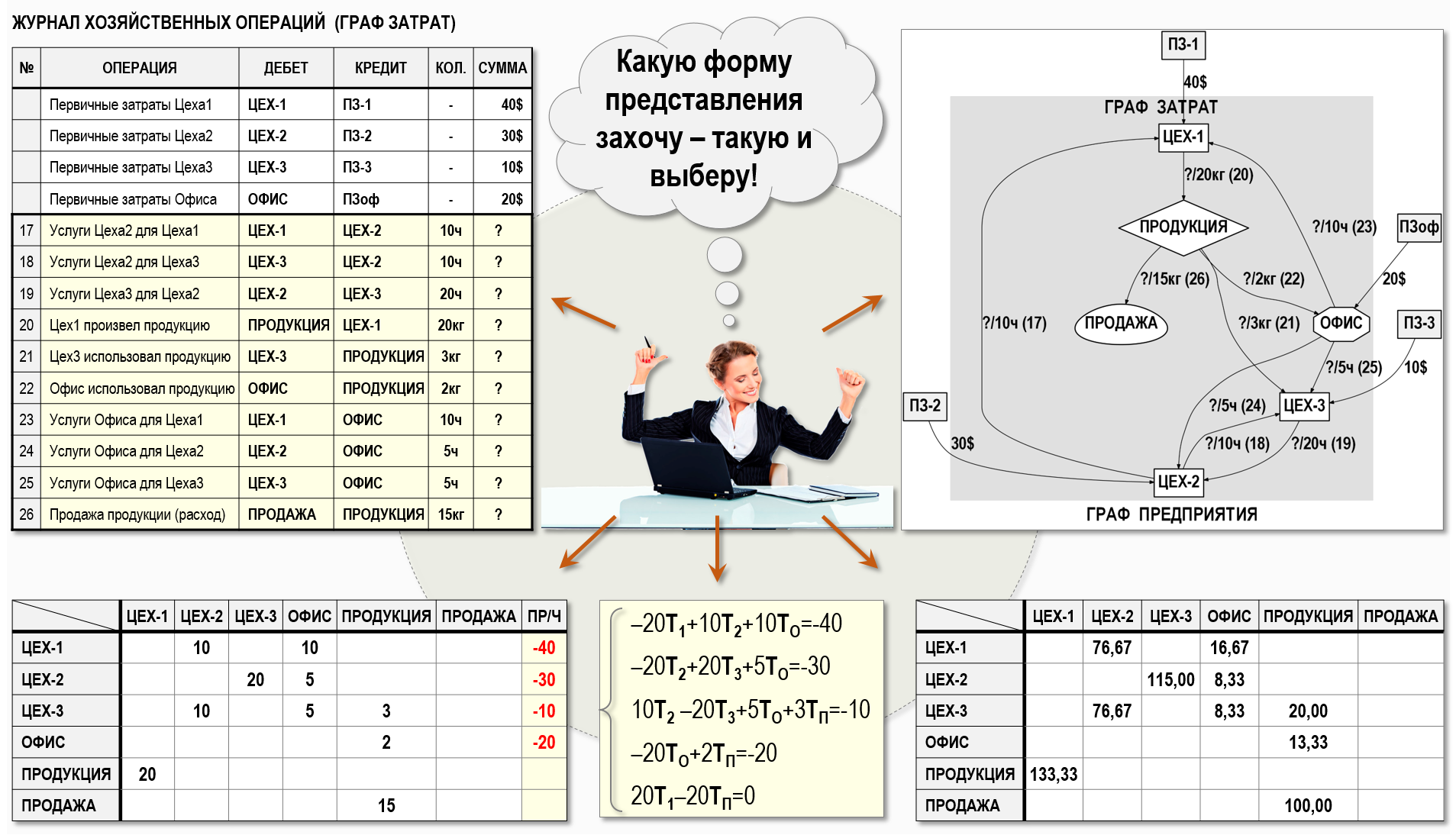
В стартовой статье данного цикла Бухгалтерский учет и теория графов мы говорили о том, что любой Граф затрат можно представить в различных формах – с помощью таблиц, элементов множеств или в графическом виде. Но на тот момент нам был известен только один вид таблиц – журнал хозяйственных операций. Теперь список таких таблиц может быть существенно расширен, в него можно включить матрицы (таблицы), рассмотренные в данной статье:
- матрица исходных коэффициентов K[6,6]
- матрица коэффициентов уравнений Р[6,6]
- матрица стоимостей С[6,6]
- вектор-столбец правых частей уравнений Z[6]
- вектор-столбец тарифов Т[6]
- расширенная матрица исходных коэффициентов KEXP[7,6]
- расширенная матрица коэффициентов уравнений PEXP[7,6]
Использование специалистом по расчету себестоимости соответствующей таблицы (матрицы) определяется характером решаемой задачи. Например, для отражения первичных учетных данных удобнее использовать журнал хозяйственных операций, а для расчета себестоимости, а также для анализа и обсуждения результатов этого расчета удобнее использовать перечисленные выше матрицы.
Важно подчеркнуть, что использование рассмотренных видов матриц (таблиц), а также графической формы представления Графов затрат позволяет сделать максимально прозрачными и понятными не только процедуру расчета себестоимости, но и последующий анализ полученных результатов. Информация о себестоимости, наглядно представленная с помощью матриц и «нарисованных» Графов затрат, воспринимается пользователями модели значительно быстрее и проще, а также, что очень важно – понимается любыми пользователями одинаково. Довольно сложно «навести тень на плетень» при обсуждении процессов формирования себестоимости на предприятии, когда перед глазами всех участников обсуждения имеется расширенная матрица исходных коэффициентов и графическое изображение Графа затрат. В данном случае общими словами (да еще которые сложно проверить) отделаться уже не получится, теперь придется обсуждать конкретные вопросы – почему используются именно такие значения исходных коэффициентов, каким образом они рассчитываются или откуда берутся, почему выбрана именно такая структура (топология) Графа затрат и т.п.
Важное практическое значение имеет также тот факт, что подобные модели, например, легко передавать «по наследству» в случае ухода с предприятия специалиста по расчету себестоимости или использовать эти модели для обучения новых сотрудников, т.к. с помощью такой модели новому специалисту значительно легче будет разобраться в тонкостях распределения затрат на предприятии, особенно, если модель еще и будет должным образом задокументирована, например, с помощью системы внутренних стандартов предприятия.
И все-таки несколько слов в конце статьи надо сказать по поводу методов решения СЛАУ, составляемых для Графов затрат. Конечно, данная тема может быть интересна не очень широкому кругу специалистов и скорее должна интересовать разработчиков автоматизированных систем, чем их пользователей. Как специалист в своей предметной области, пользователь должен решать свои профессиональные задачи, а для этого ему вполне достаточно иметь дело с «интерфейсной» частью модели, например, с расширенной матрицей исходных коэффициентов, матрицей стоимостей или с графическим изображением Графа затрат. Пользователя не должна особо интересовать «техника» формирования этих абстрактных объектов в автоматизированной системе, т.к. это является задачей разработчика.
Разработчикам же можно посоветовать использовать для решения СЛАУ методы, ориентированные на работу с сильно разреженными матрицами, т.к. наработанный на данный момент опыт работы с Графами затрат (да и здравый смысл) показывает, что расширенные матрицы исходных коэффициентов реальных Графов затрат действительно являются сильно разреженными, число ненулевых элементов в них исчисляется единицами процентов. Это вполне понятно, т.к. нет таких предприятий, в которых бы все подразделения обменивались бы вторичными затратами друг с другом. Поэтому ориентированные на работу с сильно разреженными матрицами методы могут давать выигрыш по времени решения СЛАУ для Графов затрат.
Кроме того, можно было бы рекомендовать разработчикам использовать математические библиотеки, содержащие несколько методов решения СЛАУ, т.к. пока еще нет достаточного опыта работы с Графами затрат, которым соответствуют плохо обусловленные матрицы, и в этих случаях некоторые методы могут быть численно неустойчивыми (как, например, метод Гаусса).
Также надо отметить, что математические библиотеки в современных автоматизированных системах учета должны включать в себя не только численные методы решения СЛАУ, но также и, например, алгоритмы решения задач на графах, поскольку составление и решение СЛАУ для расчета себестоимости является только одной из возможных (и далеко не самых сложных) задач на Графах затрат. Использование модели в виде Графа затрат, помимо задачи расчета себестоимости, позволяет решать и другие интересные задачи, например, определять маршруты движения потоков затрат для отдельных видов деятельности, проводить факторный анализ себестоимости, находить сценарии безубыточной работы предприятия и его отдельных видов деятельности и т.д. … и т.д. В следующей статье мы как раз и посмотрим, каким образом решение некоторых стандартных задач теории графов может оказаться полезным при работе с Графами затрат.
Вступайте в нашу телеграмм-группу Инфостарт