Совместная работа с: Владимиром Батуриным
Алгоритм раскроя построенный на симплекс-методе
На работе столкнулся с интересной задачей, нужно написать алгоритм, который из заготовочной пленки раскроит заказы клиентов с минимальным остатком. Если говорить более понятным языком, то имеем большой кусок плёнки определенной ширины и длинный, который нужно порезать на какое-то количество маленьких кусков определенной шириной и длинной, в своей статье хочу продемонстрировать свой алгоритм и услышать стороннее мнение(замечание) по нему, так как вошел в профессию недавно. Рассматривать будем на простом примере, когда у нас есть один тип пленки и из параметров только длинна и ширина(в реальных условиях могут добавляться разные параметры).
Постановка задачи:
На производстве по изготовлению пленки разработать функционал по оптимальному раскрою.
На входе имеем остатки изготовленной пленки с разными параметрами: ширина и количество(в км). И потребности клиентов с параметрами: количество(в км) и ширина.
Подробно с задачей оптимального раскроя можно ознакомиться по ссылке: https://ru.wikipedia.org/wiki/Задача_раскроя.
Решение задачи:
При разработке алгоритма раскроя принято решение воспользоваться алгоритмом решения оптимизационной задачи линейного программирования "Симплекс-метод". Подробный разбор симплекс метода можно изучить по ссылке: https://habr.com/ru/articles/474286/.
Для начала нам нужно подвести нашу задачу к каноничной форме задачи линейного программирования, для этого нам нужно создать матрицу с картами раскроя(переменная "Канон") и массив с остатками плёнки(Переменная "МассивФункции") для каждой карты раскроя. Здесь вместо кода объясню общий принцип алгоритма. К примеру имеем 2 остатка пленки и 3 потребности.
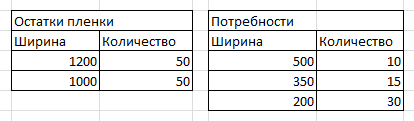
Составляем таблицу с вариантами карт раскроя(Так как при создании карт раскроя на каждом производстве свои отличия, вместо кода объясню принцип алгоритма). Для каждой пленки, из таблицы "Остатки пленки", нужно подобрать все вариации потребностей, при которых остаток для отхода не будет превышать ширину минимальной потребности.
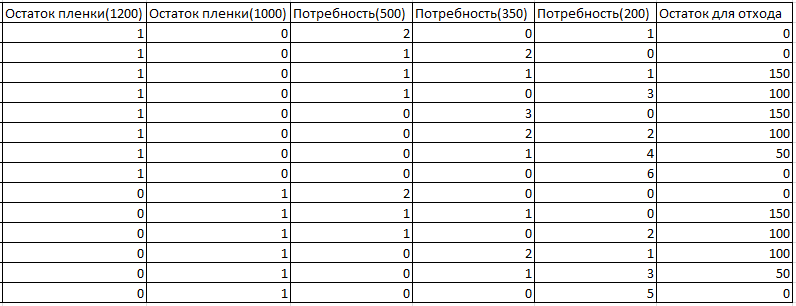
На примере первых строчек таблицы объясню заполнение. Сначала берем первый остаток(в нашем случае 1200), и начиная с большей потребности заполняем карту раскроя. В ширину 1200 вмещается две потребности по 500, тем самым остается остаток 200(1200-500*2=200). Проверяем, можем ли мы вместить еще какую-нибудь потребность, 350 не подходит, так как эта потребность больше остатка, а вот 200 нам подходит, добавляем её в нашу карту и получаем остаток 0. Переходим к следующей карте, теперь берем только одну 500, записываем её во вторую строку, в остаток у нас выходит 700. Берем следующую потребность 350, такой потребности вмещается 2 шт. Записываем в таблицу и в остаток записываем 0. Для третьей карты оставляем потребность 500, а 350 берем на 1 меньше и получаем в остатке 350(1200-500-350=350). В данный остаток вмещается только одна 200. В итоге в 3 строчке у нас имеется каждая потребность по одной штуке и остаток в 150(1200-500-350-200=150). И так пока последняя карта раскроя не будет состоять только из последней потребности(В нашем случае 200). Повторяем такой алгоритм для каждого остатка пленки.
Первые пять колонок таблицы с вариантами карт раскроя являются в моём решении переменной "Канон" и представляет собой матрицу, а шестая колонка с остатками является переменной "МассивФункции" и представляет собой массив.
Далее формируем каноничную матрицу, для этого транспонируем матрицу с картами раскроя с некоторыми изменениями:
//Переменная "Базис" вводится для заполнения последней колонки Матрицы, она показывает базисный элемент в строке(Базисный элемент всегда равен 1).
Базис = Канон.Количество() + 1;
//В алгоритме будем пользоваться методом искусственного базиса, который подразумевает добавление дополнительных ограничений, и чтобы они не вошли в наше оптимальное решение, для каждого нового ограничения добавляем в Массив Функции дополнительные элементы с большим значением(В моём примере 1000), чтобы оптимальное решение включало в себя все потребности(Ограничение типа "=");
Для индекс = 1 По Объект.ПотребностьРаскроя.Количество() Цикл
МассивФункции.Добавить(1000);
КонецЦикла;
//Так как Остатки не должны израсходоваться все, добавляем в Массив Функции дополнительные элементами со значением 0(Таким образом получаем ограничение для остатков типа "<=")
Для Каждого Остатка Из ТЗОстатки Цикл
МассивФункции.Добавить(0);
КонецЦикла;
//Формируем каноничную матрицу, в которой последняя колонка представляет собой базисные переменные(Номер строки карты раскроя из матрицы "Канон"), первая колонка представляет собой нужное количество определенной карты раскроя(на которую ссылается базис), для начального заполнения используем нужное количество потребностей(Для первой строки - количество первой потребности, для второй строки - количество второй потребности и так далее, как закончатся потребности заполняем количество Остатков)
//В последней строке матрицы Считаются дельты, начальным заполнением этой строки является Массив Функции, которую мы заполняли излишками от карт раскроя. Первое значение этой строки заполняется нулем(в дальнейшем при расчете это значение будет являться показателем целевой функции)
Для i = 0 По КолСтроки - 1 Цикл
Если i = КолСтроки - 1 Тогда
Матрица[i][0] = 0;
Матрица[i][КолКолонки - 1] = 0;
Для j = 1 По Канон.Количество() Цикл
Матрица[i][j] = МассивФункции[j];
КонецЦикла;
Иначе
Если i < Объект.ПотребностьРаскроя.Количество() Тогда
Если Объект.ПотребностьРаскроя[i].ДлинаНамотки.ДлинаНамотки = 1000 Тогда
Матрица[i][0] = Объект.ПотребностьРаскроя[i].Количество; //Было целое
Иначе
КоэфНамотки = Объект.ПотребностьРаскроя[i].ДлинаНамотки.ДлинаНамотки / 1000;
Матрица[i][0] = Объект.ПотребностьРаскроя[i].Количество / КоэфНамотки; //Было целое
КонецЕсли;
Матрица[i][КолКолонки - 1] = Базис;
Для j = 1 По Канон.Количество() Цикл
Матрица[i][j] = Канон[j - 1][i];
КонецЦикла;
Иначе
Матрица[i][0] = ТЗОстатки[i - КоличествоПотребностей].Количество; //Было целое
Матрица[i][КолКолонки - 1] = Базис;
Для j = 1 По Канон.Количество() Цикл
Матрица[i][j] = Канон[j - 1][i];
КонецЦикла;
КонецЕсли;
КонецЕсли;
Для j = Канон.Количество() + 1 По КолКолонки - 2 Цикл
Если j = Базис И i <> КолСтроки - 1 Тогда
Матрица[i][j] = 1;
Иначе
Матрица[i][j] = 0;
КонецЕсли;
КонецЦикла;
Базис = Базис + 1;
КонецЦикла;

Теперь у нас имеется готовая каноничная Матрица, каждая строка, кроме последней, является ограничением к каждой потребности и остатку. 1 строка является ограничением 1 потребности, 2 строка является ограничением 2 потребности, 3 строка является ограничением 3 потребности, 4 строка является ограничением 1 остатка и 5 строка является ограничением 2 остатка.Последняя строка заполнилась значениями из массива "МассивФункций", каждый элемент этой строки, начиная со второго, в симплекс-методе называется дельтой, а первый элемент показывает нам значение функции, с каждой итерацией симплекс-метода она должна уменьшаться, пока мы не найдем минимум функции.
Теперь можем приступать к алгоритму Симплекс-метода. Так как мы ищем оптимальные раскроя, нам нужен минимум функции, а значит у нас должны быть положительные ограничения и отрицательные дельты. Так как при формировании Матрицы у нас все ограничения получаются положительные, переходим к алгоритму, который проверяет дельты:
//Алгоритм будет работать пока все дельты не будут отрицательные, как только это случится, мы наёдем нужное решение
ЕстьПоложительныеЭлементы = Истина;
Пока ЕстьПоложительныеЭлементы Цикл
//Создаем новую матрицу в которой будем производить расчеты
Матрица2 = Новый Массив(КолСтроки, КолКолонки);
СтолбецБазиса = Неопределено;
СтрокаБазиса = 0;
СтрокаНайдена = Ложь;
//Среди элементов нижней строки матрицы выбираем максимальный положительный элемент . Столбец, в котором будет этот элемент объявляем ведущим (разрешающим).
Для j = 1 По КолКолонки - 2 Цикл
Если Окр(Матрица[КолСтроки - 1][j], 5) > 0 Тогда
МаксимальныйБазис = Матрица[КолСтроки - 1][j];
СтолбецБазиса = j;
Прервать;
КонецЕсли;
КонецЦикла;
Если НЕ СтолбецБазиса = Неопределено Тогда
Для j = СтолбецБазиса + 1 По КолКолонки - 2 Цикл
Если Окр(Матрица[КолСтроки - 1][j], 5) > Окр(МаксимальныйБазис) Тогда
МаксимальныйБазис = Матрица[КолСтроки - 1][j];
СтолбецБазиса = j;
КонецЕсли;
КонецЦикла;
КонецЕсли;
//Если Положительных элементов не оказалось, завершаем алгоритм
Если СтолбецБазиса = Неопределено Тогда
Прервать;
КонецЕсли;
//После того, как нашли максимальный положительный элемент, в этом столбце выбираем элемент, который будем превращать в базис
//Левый столбец почленно делится на ведущий столбец(который мы выбрали в прошлом шаге)
//Среди полученных значений выбирают минимальное положительное (отрицательные и нулевые ответы не рассматривают)
МинимальныйБазис = 0.001;
Для i = 0 По КолСтроки - 2 Цикл
Если Матрица[i][СтолбецБазиса] > 0 Тогда
Если СтрокаНайдена Тогда
Если Матрица[СтрокаБазиса][0] / МинимальныйБазис > Матрица[i][0] / Матрица[i][СтолбецБазиса]
И Матрица[i][0] / Матрица[i][СтолбецБазиса] > 0 Тогда
МинимальныйБазис = Матрица[i][СтолбецБазиса];
СтрокаБазиса = i;
КонецЕсли;
Иначе
Если 1 / МинимальныйБазис > Матрица[i][0] / Матрица[i][СтолбецБазиса]
И Матрица[i][0] / Матрица[i][СтолбецБазиса] > 0 Тогда
МинимальныйБазис = Матрица[i][СтолбецБазиса];
СтрокаБазиса = i;
СтрокаНайдена = Истина;
КонецЕсли;
КонецЕсли;
КонецЕсли;
КонецЦикла;
//Если при расчетах мы не нашли удовлетворяющий нам вариант, прекращаем алгоритм, так как решения нет
Если СтрокаНайдена = Ложь Тогда
Сообщить("С текущими входными данными оптимального решения нет!");
РешениеЕсть = Ложь;
Прервать;
КонецЕсли;
//Если мы нашли подходящую строку, объявляем ведущий элемент, который будем превращать в базис.
ВедущийЭлемент = Матрица[СтрокаБазиса][СтолбецБазиса];
//Всю строку делим на ведущий элемент, чтобы получить единицу
Для j = 0 По КолКолонки - 2 Цикл
Матрица2[СтрокаБазиса][j] = Окр(Матрица[СтрокаБазиса][j] / ВедущийЭлемент, 10);
КонецЦикла;
//Далее каждую строку нужно перерассчитать по формуле: ЭлементСтроки[n] - ЭлементСтроки[СтолбецБазиса] * ЭлементБазиснойСтроки[n]
Переменная2 = Матрица2[СтрокаБазиса];
Для i = 0 По КолСтроки - 2 Цикл
Переменная = Матрица[i][СтолбецБазиса];
Переменная3 = Матрица[i];
Если i = СтрокаБазиса Тогда
Продолжить;
Иначе
Для j = 0 По КолКолонки - 2 Цикл
Матрица2[i][j] = Окр(Переменная3[j] - Переменная * Переменная2[j], 10);
КонецЦикла;
Матрица2[i][КолКолонки - 1] = Матрица[i][КолКолонки - 1];
КонецЕсли;
КонецЦикла;
//Приравниваем последнему элементу в базисной строке индекс базисной переменной
Матрица2[СтрокаБазиса][КолКолонки - 1] = СтолбецБазиса;
Выгружаем наши расчеты в основную матрицу
сз = Новый СписокЗначений;
сз.ЗагрузитьЗначения(Матрица2);
Матрица = сз.ВыгрузитьЗначения();
//перерасчет дельт
Для j = 0 По МассивФункции.Количество() - 1 Цикл
Элемент = Матрица[0][КолКолонки - 1];
Переменная = МассивФункции[Элемент] * Матрица[0][j];
Для i = 1 По КолСтроки - 2 Цикл
Элемент = Матрица[i][КолКолонки - 1];
Переменная = Переменная + МассивФункции[Элемент] * Матрица[i][j];
КонецЦикла;
Матрица[КолСтроки - 1][j] = Окр(Переменная - МассивФункции[j], 1);;
КонецЦикла;
//после каждой итерации проверяем план на оптимальность, то-есть смотрим, чтобы не было отрицательных ограничений
ПроверкаНаПоложительныеОграничения(Матрица, КолСтроки, КолКолонки, МассивФункции, Канон);
КонецЦикла;
В процедуре ПроверкаНаПоложительныеОграничения() проверяем, чтобы в первой колонке матрицы не было отрицательных элементов, если такие элементы присутствуют перерассчитываем матрицу
//Переменная ПроверкаДельт нужна для проверки условия, если мы не нашли отрицательные элементы в колонке, то и пересчет дельт не нужен
ПроверкаДельт = Ложь;
Пока ЕстьОтрицательныеЭлементы Цикл
Матрица2 = Новый Массив(КолСтроки, КолКолонки);
МинимальныйБазис1 = Матрица[0][0];
СтрокаБазиса = 0;
СтолбецБазиса = 1;
//Циклом находим минимальный элемент в первой колонке
Для i = 1 По КолСтроки - 2 Цикл
Если МинимальныйБазис1 > Матрица[i][0] Тогда
МинимальныйБазис1 = Матрица[i][0];
СтрокаБазиса = i;
КонецЕсли
КонецЦикла;
//Если минимальный элемент положительны, прекращаем вычисления и возвращаемся к поиску положительных дельт
Если МинимальныйБазис1 >= 0 Тогда
Прервать;
КонецЕсли;
ПроверкаДельт = Истина;
//Если находим отрицательный элемент, проводим расчёты, для этого ищем подходящий минимальный элемент в найденной строке
МинимальныйБазис2 = Матрица[СтрокаБазиса][1];
Для j = 2 По КолКолонки - 2 Цикл
Если МинимальныйБазис2 > Матрица[СтрокаБазиса][j] Тогда
МинимальныйБазис2 = Матрица[СтрокаБазиса][j];
СтолбецБазиса = j;
КонецЕсли;
КонецЦикла;
//Как только находим нужный элемент, фиксируем его в переменной, и объявляем ведущим(Делаем из него базисный элемент)
ВедущийЭлемент = Матрица[СтрокаБазиса][СтолбецБазиса];
//Проводим такие-же вычисления как и в алгоритме по поиску положительных дельт
Для j = 0 По КолКолонки - 2 Цикл
Матрица2[СтрокаБазиса][j] = Окр(Матрица[СтрокаБазиса][j] / ВедущийЭлемент, 10);
КонецЦикла;
Для i = 0 По КолСтроки - 2 Цикл
Переменная = Матрица[i][СтолбецБазиса];
Если i = СтрокаБазиса Тогда
Продолжить;
Иначе
Для j = 0 По КолКолонки - 2 Цикл
Матрица2[i][j] = Окр(Матрица[i][j] - Переменная * Матрица2[СтрокаБазиса][j], 10);
КонецЦикла;
Матрица2[i][КолКолонки - 1] = Матрица[i][КолКолонки - 1];
КонецЕсли;
КонецЦикла;
Матрица2[СтрокаБазиса][КолКолонки - 1] = СтолбецБазиса;
сз = Новый СписокЗначений;
сз.ЗагрузитьЗначения(Матрица2);
Матрица = сз.ВыгрузитьЗначения();
КонецЦикла;
Если ПроверкаДельт = Истина Тогда
//перерасчет дельт
Для j = 0 По МассивФункции.Количество() - 1 Цикл
Элемент = Матрица[0][КолКолонки - 1];
Переменная = МассивФункции[Элемент] * Матрица[0][j];
Для i = 1 По КолСтроки - 2 Цикл
Элемент = Матрица[i][КолКолонки - 1];
Переменная = Переменная + МассивФункции[Элемент] * Матрица[i][j];
КонецЦикла;
Матрица[КолСтроки - 1][j] = Окр(Переменная - МассивФункции[j], 1);
КонецЦикла;
КонецЕсли;
Как только в матрице все дельты станут отрицательные, а ограничения положительные, значит алгоритм нашёл решение, но оно является нецелочисленным.

В последней колонке представлены номера карт раскроя, например в первой строке видим значение 1, значит это первая карта раскроя(0 индекс в массиве Канон), а в первой колонке представлено количество этих карт. На примере первой строки, получается, что нам нужно 1,25 первой карты раскроя. Также можем видеть, что в последней колонке есть значения 18 и 19, которые не входят в границы массива "Канон". Такие строки не учитываются в конечном решении.
Для преобразования решения в целочисленное, используем упрощённый вариант алгоритма округления:
Для Каждого СтрокаМатрицы Из Матрица Цикл
СтрокаМатрицы[0] = Окр(СтрокаМатрицы[0]);
КонецЦикла;
В итоге получаем 1 шт. первой карты раскроя, 8 шт. второй и 5 шт. восьмой

Вступайте в нашу телеграмм-группу Инфостарт