Беллман-Форд в 1С: Оптимизация с отрицательными весами
Статья посвящена реализации алгоритма Беллмана-Форда на платформе 1С 8.3. Рассматривается применение алгоритма для поиска кратчайших путей в графах с ребрами, имеющими отрицательный вес. Приведен пример кода и показаны практические сценарии использования.
В задачах оптимизации маршрутов часто требуется найти кратчайший путь между двумя точками. Для решения таких задач существует множество алгоритмов, одним из самых известных является алгоритм Дейкстры. Однако алгоритм Дейкстры не работает с графами, содержащими ребра с отрицательным весом. В таких случаях на помощь приходит алгоритм Беллмана-Форда. В данной статье мы рассмотрим реализацию алгоритма Беллмана-Форда на платформе 1С 8.3, покажем, как его можно использовать для решения практических задач, и приведем пример кода.
Что такое алгоритм Беллмана-Форда?
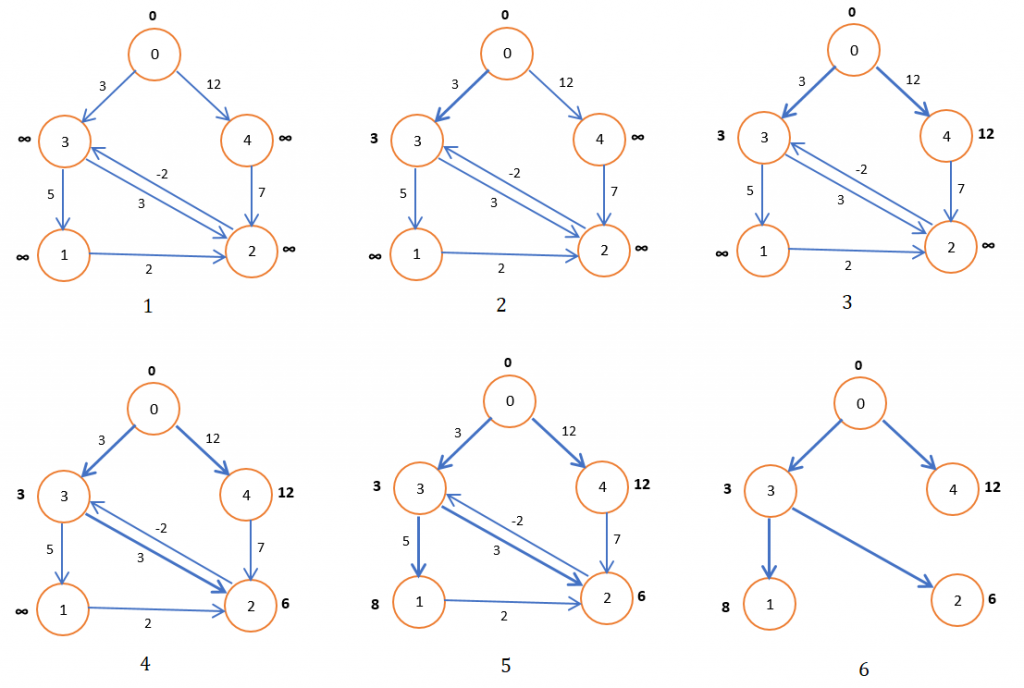
Алгоритм Беллмана-Форда – это алгоритм поиска кратчайшего пути во взвешенном графе. В отличие от алгоритма Дейкстры, он может работать с графами, содержащими ребра с отрицательным весом. Алгоритм также позволяет определить, есть ли в графе цикл отрицательного веса (цикл, сумма весов ребер которого отрицательна), наличие которого делает задачу поиска кратчайшего пути бессмысленной.
Алгоритм Беллмана-Форда работает путем последовательной релаксации ребер графа. Релаксация ребра – это процесс обновления оценки кратчайшего пути до конечной вершины ребра, если найден более короткий путь через начальную вершину ребра. Алгоритм выполняет |V| - 1 итераций (где |V| – количество вершин в графе), на каждой итерации релаксируя все ребра графа. После |V| - 1 итераций, если после очередной релаксации ребер расстояние до какой-либо вершины уменьшилось, значит, в графе есть цикл отрицательного веса.
Практическое применение алгоритма Беллмана-Форда:
Алгоритм Беллмана-Форда может быть использован для решения различных задач, в которых требуется найти кратчайший путь во взвешенном графе, содержащем ребра с отрицательным весом. Вот несколько примеров:
- Финансовый анализ: Поиск арбитражных возможностей на валютном рынке. В этом случае вершины графа представляют валюты, а ребра – обменные курсы. Отрицательный вес ребра может соответствовать комиссии за обмен.
- Оптимизация маршрутов с учетом скидок и штрафов: В задачах логистики и доставки отрицательный вес может представлять скидку на транспортировку между определенными пунктами.
- Анализ сетевых протоколов: Поиск кратчайших путей в сетях с переменной пропускной способностью, где отрицательный вес может представлять увеличение пропускной способности.
Ниже приведен пример реализации алгоритма Беллмана-Форда на платформе 1С 8.3. В данном примере граф задается программно в виде соответствия, где ключи – это вершины (города), а значения – другие соответствия, представляющие ребра, исходящие из данной вершины, и их веса (расстояния).
&НаСервере
Функция НайтиКратчайшийПутьБеллманаФорда(Граф, НачальныйГород, КонечныйГород, Бесконечность)
// 1. Инициализация
distances = Новый Соответствие();
previous = Новый Соответствие();
Для Каждого ЭлементГрафа Из Граф Цикл
город = ЭлементГрафа.Ключ;
distances.Вставить(город, Число(Бесконечность));
previous.Вставить(город, "");
КонецЦикла;
distances[НачальныйГород] = 0;
// 2. Основной цикл алгоритма (релаксация ребер)
Для Индекс = 1 По Граф.Количество() - 1 Цикл
Для Каждого ЭлементГрафа Из Граф Цикл
sourceCity = ЭлементГрафа.Ключ;
Для Каждого Сосед Из Граф[sourceCity] Цикл
destinationCity = Сосед.Ключ;
weight = Сосед.Значение;
Если distances[sourceCity] <> Число(Бесконечность) И distances[sourceCity] + weight < distances[destinationCity] Тогда
distances[destinationCity] = distances[sourceCity] + weight;
previous[destinationCity] = sourceCity;
КонецЕсли;
КонецЦикла;
КонецЦикла;
КонецЦикла;
// 3. Проверка наличия цикла отрицательного веса
Для Каждого ЭлементГрафа Из Граф Цикл
sourceCity = ЭлементГрафа.Ключ;
Для Каждого Сосед Из Граф[sourceCity] Цикл
destinationCity = Сосед.Ключ;
weight = Сосед.Значение;
Если distances[sourceCity] <> Число(Бесконечность) И distances[sourceCity] + weight < distances[destinationCity] Тогда
// Обнаружен цикл отрицательного веса
Возврат Неопределено;
КонецЕсли;
КонецЦикла;
КонецЦикла;
// 4. Восстановление пути
Путь = Новый Массив();
currentCity = КонечныйГород;
Пока currentCity <> "" Цикл
Путь.Вставить(1, currentCity);
currentCity = previous[currentCity];
КонецЦикла;
// 5. Формируем строку пути
СтрокаПути = СтрСоединить(Путь, " -> ");
// 6. Возвращаем результаты
Результаты = Новый Структура("Путь, Длина", СтрокаПути, distances[КонечныйГород]);
Возврат Результаты;
КонецФункции
Вспомогательный код для запуска алгоритма (процедура обработки команды на форме):
&НаСервере
Процедура ЗапуститьАлгоритмНаСервере()
// 0. Определяем константу "Бесконечность"
Бесконечность = 1000000; // или другое достаточно большое число
// 1. Задаем граф (программно)
Граф = Новый Соответствие();
// Добавляем вершины (города)
Граф.Вставить("Город1", Новый Соответствие());
Граф.Вставить("Город2", Новый Соответствие());
Граф.Вставить("Город3", Новый Соответствие());
Граф.Вставить("Город4", Новый Соответствие());
// Добавляем ребра (расстояния между городами)
// Внимание! Добавляем ребро с отрицательным весом!
Граф["Город1"].Вставить("Город2", 10);
Граф["Город1"].Вставить("Город3", 15);
Граф["Город2"].Вставить("Город1", 10);
Граф["Город2"].Вставить("Город3", 8);
Граф["Город2"].Вставить("Город4", 20);
Граф["Город3"].Вставить("Город1", 15);
Граф["Город3"].Вставить("Город2", 8);
Граф["Город3"].Вставить("Город4", 5);
Граф["Город4"].Вставить("Город2", 20);
Граф["Город4"].Вставить("Город3", -5); // Отрицательный вес!
// 2. Указываем начальный и конечный город
НачальныйГород = "Город1";
КонечныйГород = "Город4";
// 3. Запускаем алгоритм Беллмана-Форда
Результаты = НайтиКратчайшийПутьБеллманаФорда(Граф, НачальныйГород, КонечныйГород, Бесконечность);
// 4. Выводим результаты в окно сообщений
Если Результаты <> Неопределено Тогда
Сообщить("Кратчайший путь: " + Результаты.Путь);
Сообщить("Длина пути: " + Результаты.Длина);
Иначе
Сообщить("Путь из " + НачальныйГород + " в " + КонечныйГород + " не найден или обнаружен цикл отрицательного веса.");
КонецЕсли;
КонецПроцедуры
&НаКлиенте
Процедура ЗапуститьАлгоритм(Команда)
ЗапуститьАлгоритмНаСервере();
КонецПроцедуры
Описание кода:
- Функция НайтиКратчайшийПутьБеллманаФорда принимает на вход граф, начальный город, конечный город и значение “бесконечности”.
- Функция инициализирует расстояния до всех городов значением “бесконечности”, а расстояние до начального города – нулем.
- Основной цикл алгоритма выполняется |V| - 1 раз, где |V| – количество городов.
- Внутри цикла происходит релаксация всех ребер графа.
- После завершения основного цикла происходит проверка наличия цикла отрицательного веса.
- Если цикл отрицательного веса не обнаружен, функция восстанавливает кратчайший путь и возвращает его и его длину.
- Если цикл отрицательного веса обнаружен, функция возвращает Неопределено
Почему расстояние может быть -5?
Очень важный вопрос! Действительно, понятие “расстояние” в обычном понимании не может быть отрицательным. Расстояние – это физическая величина, характеризующая протяжённость между двумя точками, и она всегда неотрицательна.
Однако, в контексте алгоритма Беллмана-Форда, отрицательные веса ребер графа могут использоваться для моделирования различных ситуаций, не связанных напрямую с физическим расстоянием. Вот несколько примеров:
-
Прибыль/Убыток: В задачах финансового планирования, вес ребра может представлять не расстояние, а прибыль (положительное значение) или убыток (отрицательное значение) от перехода из одного состояния в другое. Алгоритм Беллмана-Форда в этом случае будет искать путь, максимизирующий прибыль (или минимизирующий убытки).
-
Скидки/Штрафы: В задачах логистики и доставки, отрицательный вес может представлять скидку на транспортировку между определенными пунктами, а положительный вес - штраф.
-
Моделирование изменений: Отрицательные веса можно использовать для моделирования изменений в системе. Например, если алгоритм используется для планирования производства, отрицательный вес может представлять уменьшение запасов сырья при переходе от одного этапа производства к другому.
-
Обнаружение арбитража: В финансовых приложениях, алгоритм Беллмана-Форда может использоваться для обнаружения возможностей арбитража на валютном рынке. Отрицательный цикл в графе будет указывать на возможность получить прибыль, конвертируя валюту по определенному кругу.
Важно помнить:
- Алгоритм Дейкстры не работает с отрицательными весами, так как он предполагает, что добавление новых ребер всегда увеличивает длину пути.
- Алгоритм Беллмана-Форда позволяет обрабатывать отрицательные веса, но он также способен обнаруживать циклы отрицательного веса (циклы в графе, сумма весов ребер которых отрицательна). Наличие такого цикла означает, что не существует кратчайшего пути (потому что можно бесконечно “наматывать” круги по этому циклу, каждый раз уменьшая длину пути).
В нашем примере с городами, отрицательное “расстояние” между городами 4 и 3 можно интерпретировать, например, как доплату за проезд по этому маршруту (вместо платы за проезд). То есть, если вы проедете из города 4 в город 3, вы получите 5 единиц (например, валюты) вместо того, чтобы платить. Это, конечно, не физическое расстояние, но вполне допустимая модель для алгоритма Беллмана-Форда.
Алгоритм Беллмана-Форда – это мощный инструмент для поиска кратчайших путей во взвешенном графе, который может работать с ребрами, имеющими отрицательный вес. В данной статье мы рассмотрели реализацию алгоритма Беллмана-Форда на платформе 1С 8.3 и показали, как его можно использовать для решения практических задач. Приведенный пример кода может быть использован в качестве основы для разработки более сложных и специализированных решений.
Тестирование и настройка:
Алгоритм Беллмана-Форда, представленный в этой статье, был протестирован на платформе 1С:Предприятие 8.3 (версия 8.3.23.1862). Для тестирования использовалась форма внешней обработки.
Настройка данных для тестирования:
Для изменения данных, используемых алгоритмом, необходимо внести изменения в процедуру ЗапуститьАлгоритмНаСервере(). В этой процедуре программно задается граф, начальный и конечный города.
- Изменение городов и расстояний: В разделе // 1. Задаем граф (программно) можно изменить список городов и расстояния между ними.
// Добавляем вершины (города) Граф.Вставить("Город1", Новый Соответствие()); Граф.Вставить("Город2", Новый Соответствие()); Граф.Вставить("Город3", Новый Соответствие()); Граф.Вставить("Город4", Новый Соответствие()); // Добавляем ребра (расстояния между городами) // Внимание! Добавляем ребро с отрицательным весом! Граф["Город1"].Вставить("Город2", 10); Граф["Город1"].Вставить("Город3", 15); Граф["Город2"].Вставить("Город1", 10); Граф["Город2"].Вставить("Город3", 8); Граф["Город2"].Вставить("Город4", 20); Граф["Город3"].Вставить("Город1", 15); Граф["Город3"].Вставить("Город2", 8); Граф["Город3"].Вставить("Город4", 5); Граф["Город4"].Вставить("Город2", 20); Граф["Город4"].Вставить("Город3", -5); // Отрицательный вес! - Для добавления нового города, добавьте строку Граф.Вставить("НовыйГород", Новый Соответствие());. Для добавления расстояния между городами, добавьте строку Граф["Город1"].Вставить("Город2", 25);, где "Город1" – начальный город, "Город2" – конечный город, а 25– расстояние между ними. Помните: расстояния надо указывать в обе стороны, если это необходимо.
- Изменение начального и конечного города: В разделе // 2. Указываем начальный и конечный город можно изменить начальный и конечный город для поиска кратчайшего пути.
// 2. Указываем начальный и конечный город НачальныйГород = "Город1"; КонечныйГород = "Город4";Просто измените значения переменных НачальныйГород и КонечныйГород на желаемые.
При изменении данных убедитесь, что все города, указанные в расстояниях, существуют в списке городов. В противном случае алгоритм может работать некорректно. Также, для наглядности, вы можете добавить вывод графа в окно сообщений перед запуском алгоритма.
Изменяя эти параметры, вы сможете протестировать алгоритм на различных сценариях и убедиться в его правильной работе.
Вступайте в нашу телеграмм-группу Инфостарт