Алгоритм Форда-Фалкерсона
Пример (упрощенная модель поставок между складами):
Допустим, у вас есть три склада: Центральный (источник), Склад 1 и Склад 2 (сток).
- Центральный -> Склад 1: пропускная способность 100 единиц товара
- Центральный -> Склад 2: пропускная способность 80 единиц товара
- Склад 1 -> Склад 2: пропускная способность 50 единиц товара
Алгоритм Форда-Фалкерсона поможет определить, как оптимально доставить товар со склада Центральный на склад Склад 2, учитывая ограничения пропускной способности.
Алгоритм Форда-Фалкерсона - это алгоритм для решения задачи о максимальном потоке в транспортной сети. Транспортная сеть - это граф (набор узлов, связанных ребрами), где каждому ребру приписана пропускная способность (максимальное количество “чего-то”, что может пройти по этому ребру). Задача состоит в том, чтобы определить, какое максимальное количество “чего-то” можно переправить из заданного узла-источника в заданный узел-сток, учитывая пропускные способности всех ребер сети.
Применение алгоритма Форда-Фалкерсона в 1С (возможные сценарии):
Хотя 1С и не является платформой для решения сложных математических задач, алгоритм Форда-Фалкерсона можно применить в некоторых специфических сценариях, где важна оптимизация потоков ресурсов:
-
Оптимизация поставок между складами (упрощенная модель):
Представьте, что у вас есть несколько складов (узлы графа) и каналы поставок между ними (ребра графа) с ограниченной пропускной способностью (например, максимальное количество машин в день). Нужно определить, как оптимально перераспределить товары с центрального склада (источник) на склад, где возник дефицит (сток), чтобы максимизировать объем поставки.
-
Распределение задач между сотрудниками (упрощенная модель):
Рассмотрим задачу распределения задач между сотрудниками отдела. У каждого сотрудника есть определенная "пропускная способность" - количество задач, которые он может выполнить за день. Каждая задача требует определенных навыков и может быть выполнена только определенными сотрудниками. Алгоритм Форда-Фалкерсона может помочь найти оптимальное распределение задач, чтобы максимизировать количество выполненных задач за день.
-
Оптимизация использования производственных мощностей (очень упрощенная модель):
Представьте, что у вас есть несколько производственных линий (узлы графа) и каналы передачи полуфабрикатов между ними (ребра графа) с ограниченной пропускной способностью. Нужно определить, как оптимально организовать передачу полуфабрикатов от одной линии к другой, чтобы максимизировать выпуск готовой продукции.
Важные моменты при реализации в 1С:
- Упрощение модели: В реальных задачах логистики или производства слишком много факторов, чтобы их учесть в простой модели транспортной сети. Поэтому нужно сильно упрощать модель, чтобы её можно было решить с помощью алгоритма Форда-Фалкерсона.
- Ограничения 1С: 1С не предназначена для сложных вычислений, поэтому алгоритм может работать медленно на больших графах.
- Визуализация: Важно визуализировать результаты работы алгоритма (например, на схеме складов или производственных линий), чтобы пользователи могли понять, как распределяются потоки ресурсов.
Алгоритм Форда-Фалкерсона может быть полезен в 1С для решения задач оптимизации потоков ресурсов, но его применение ограничено из-за упрощений, необходимых для моделирования реальных бизнес-процессов, и ограничений самой платформы 1С. Тем не менее, в некоторых специфических сценариях он может помочь найти оптимальное решение и повысить эффективность работы предприятия.
1. Постановка задачи и математическая модель (основные понятия):
- Что такое задача о максимальном потоке в транспортной сети (определение, примеры).
- Основные элементы: узлы (источник, сток, промежуточные), ребра, пропускная способность.
- Формальное определение задачи: максимизировать поток из источника в сток, не превышая пропускную способность ребер.
- Примеры бизнес-задач (поставки, распределение задач), с акцентом на упрощения для применимости в 1С.
2. Алгоритм Форда-Фалкерсона: пошаговое описание:
- Общая идея: поиск увеличивающих путей и увеличение потока.
- Этапы: инициализация, основной цикл (поиск пути, определение минимума, увеличение потока), критерий остановки.
- Алгоритм BFS для поиска увеличивающего пути. (О алгоритме с примером рабочей обработки для 1с v8.3 писал ранее в этой статье: Поиск пути на складе в 1С 8.3: реализация алгоритма волновой трассировки для управления логистикой )
3. Реализация алгоритма Форда-Фалкерсона в 1С (с подробным описанием кода):
- Представление графа (матрица смежности):
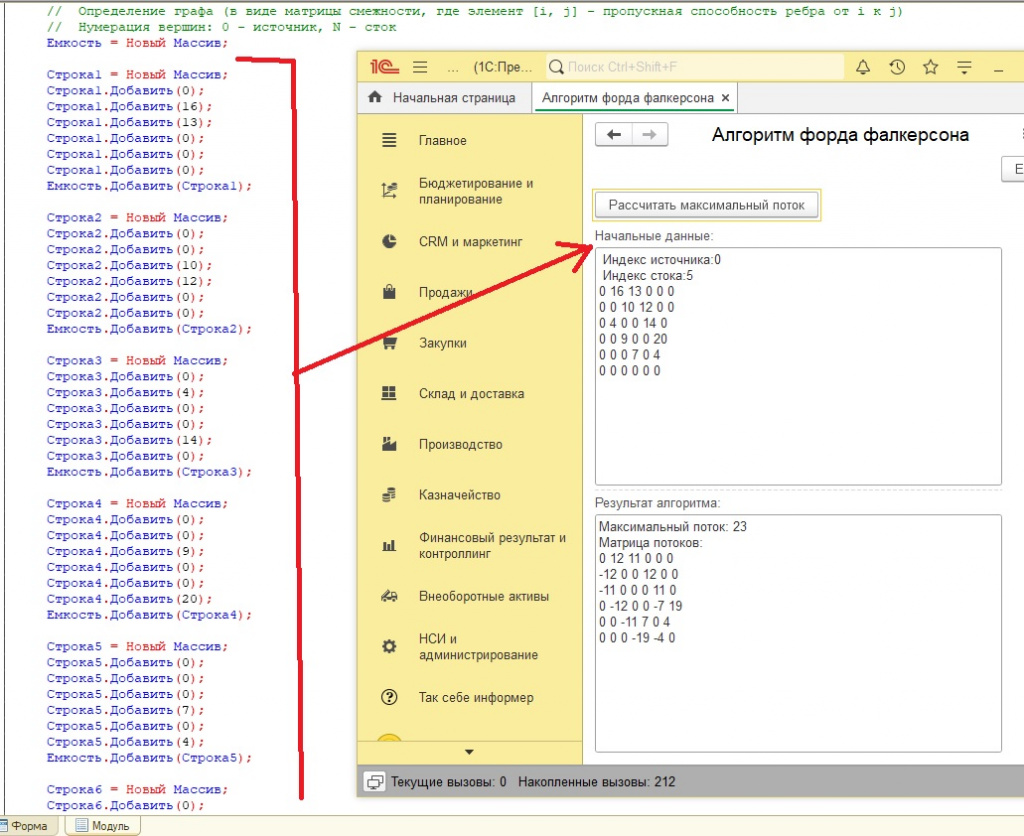
Емкость = Новый Массив; // (Далее идет код инициализации матрицы смежности)Описываем, что матрица смежности хранит пропускные способности ребер.
Строка1 = Новый Массив; Строка1.Добавить(0); Строка1.Добавить(16); Строка1.Добавить(13); Строка1.Добавить(0); Строка1.Добавить(0); Строка1.Добавить(0); Емкость.Добавить(Строка1); Строка2 = Новый Массив; Строка2.Добавить(0); Строка2.Добавить(0); Строка2.Добавить(10); Строка2.Добавить(12); Строка2.Добавить(0); Строка2.Добавить(0); Емкость.Добавить(Строка2); // и т.д. -
Функция НайтиУвеличивающийПуть(Емкость, Поток, Источник, Сток):
Важным этапом является поиск увеличивающего пути, то есть пути от источника к стоку, по которому можно "протолкнуть" дополнительный поток. Для этого в нашей реализации используется функция "НайтиУвеличивающийПуть(Емкость, Поток, Источник, Сток)". Эта функция реализует алгоритм поиска в ширину (BFS - Breadth-First Search), который позволяет найти кратчайший (в смысле количества ребер) путь между двумя узлами графа.
Алгоритм BFS работает следующим образом: он начинает поиск с исходного узла (источника) и постепенно расширяет область поиска, добавляя в очередь соседние узлы. При этом он отслеживает, какие узлы уже были посещены, чтобы избежать зацикливания. В нашей реализации эта информация хранится в массиве "Посещенные". Если элемент "Посещенные[i]" равен Истина, это означает, что узел с индексом "i" уже был посещен алгоритмом.
Для восстановления найденного пути используется массив "Предшественник". Этот массив хранит информацию о том, из какого узла мы пришли в текущий узел. Например, если "Предшественник[3] = 2", это означает, что мы попали в узел с индексом 3 из узла с индексом 2. Зная предшественника для каждого узла на пути от стока к источнику, мы можем легко восстановить весь путь, двигаясь в обратном направлении. Если "Предшественник[i] = Неопределено", это означает, что в узел "i" мы еще не пришли или он является источником.
// Функция поиска увеличивающего пути с помощью BFS
Функция НайтиУвеличивающийПуть(Емкость, Поток, Источник, Сток)
КоличествоВершин = Емкость.Количество();
Посещенные = Новый Массив;
Для i = 0 По КоличествоВершин - 1 Цикл
Посещенные.Добавить(Ложь);
КонецЦикла;
Очередь = Новый Массив;
Очередь.Добавить(Источник);
Посещенные[Источник] = Истина;
Предшественник = Новый Массив;
Для i = 0 По КоличествоВершин - 1 Цикл
Предшественник.Добавить(Неопределено);
КонецЦикла;
Пока Очередь.Количество() > 0 Цикл
Вершина = Очередь[0];
Очередь.Удалить(0);
Если Вершина = Сток Тогда
// Достигли стока, путь найден
Путь = Новый Массив;
ТекущаяВершина = Сток;
Пока ТекущаяВершина <> Неопределено Цикл
Путь.Вставить(0, ТекущаяВершина);
ТекущаяВершина = Предшественник[ТекущаяВершина];
КонецЦикла;
Возврат Путь;
КонецЕсли;
Для Сосед = 0 По КоличествоВершин - 1 Цикл
Если Не Посещенные[Сосед] И Емкость[Вершина][Сосед] - Поток[Вершина][Сосед] > 0 Тогда
Очередь.Добавить(Сосед);
Посещенные[Сосед] = Истина;
Предшественник[Сосед] = Вершина;
КонецЕсли;
КонецЦикла;
КонецЦикла;
// Не удалось найти путь
Возврат Неопределено;
КонецФункции
- Основной цикл алгоритма в процедуре РассчитатьМаксимальныйПоток(Команда):
Пока Истина Цикл УвеличивающийПуть = НайтиУвеличивающийПуть(Емкость, Поток, Источник, Сток); Если УвеличивающийПуть = Неопределено Тогда Прервать; // Нет путей, завершаем КонецЕсли; //(Код определения минимальной пропускной способности) //(Код увеличения потока) КонецЦикла;Основная работа алгоритма Форда-Фалкерсона происходит в цикле, который выполняется до тех пор, пока в транспортной сети существуют увеличивающие пути, то есть пути, по которым можно увеличить общий поток от источника к стоку. Логика цикла состоит из нескольких ключевых шагов:
1. Поиск увеличивающего пути: На каждом шаге цикла мы вызываем функцию "НайтиУвеличивающийПуть", которую описали ранее. Эта функция пытается найти путь от источника к стоку, используя алгоритм BFS. Если такой путь существует, функция возвращает массив узлов, составляющих этот путь. В противном случае функция возвращает "Неопределено", что сигнализирует о том, что больше увеличивающих путей нет.
2. Проверка наличия пути: После вызова функции "НайтиУвеличивающийПуть" мы проверяем, был ли найден путь. Если функция вернула "Неопределено", это означает, что мы достигли максимального потока и цикл можно завершить. В коде это выглядит так:
УвеличивающийПуть = НайтиУвеличивающийПуть(Емкость, Поток, Источник, Сток); Если УвеличивающийПуть = Неопределено Тогда Прервать; // Нет путей, завершаем КонецЕсли;3. Определение минимальной пропускной способности: Если путь был найден, следующим шагом является определение минимальной пропускной способности на этом пути. Это необходимо для того, чтобы определить, какое максимальное количество потока мы можем "протолкнуть" по этому пути, не превышая пропускную способность ни одного из ребер. Мы проходим по всем ребрам найденного пути и находим ребро с наименьшей пропускной способностью, учитывая текущий поток по этому ребру.
4. Увеличение потока вдоль пути: После того, как мы определили минимальную пропускную способность, мы увеличиваем поток по всем ребрам найденного пути на эту величину. Это означает, что мы увеличиваем значение "Поток[i][j]" для каждого ребра (i, j) на пути.
5. Обработка обратных ребер: Важным моментом в алгоритме Форда-Фалкерсона является обработка обратных ребер. Для каждого ребра (i, j) на найденном пути мы также уменьшаем поток в обратном направлении, то есть уменьшаем значение "Поток[j][i]" на ту же величину. Это позволяет алгоритму "отменять" ранее отправленный поток, если это необходимо для поиска оптимального решения. Обратные ребра позволяют алгоритму перераспределять поток по сети, чтобы найти максимальный поток. Например, если мы сначала отправили поток по не самому оптимальному пути, обратные ребра позволяют "вернуть" часть этого потока и направить его по более выгодному пути.
&НаКлиенте
Процедура РассчитатьМаксимальныйПоток(Команда)
Бесконечность = 100000;
// Определение графа (в виде матрицы смежности, где элемент [i, j] - пропускная способность ребра от i к j)
// Нумерация вершин: 0 - источник, N - сток
Емкость = Новый Массив;
Строка1 = Новый Массив;
Строка1.Добавить(0);
Строка1.Добавить(16);
Строка1.Добавить(13);
Строка1.Добавить(0);
Строка1.Добавить(0);
Строка1.Добавить(0);
Емкость.Добавить(Строка1);
Строка2 = Новый Массив;
Строка2.Добавить(0);
Строка2.Добавить(0);
Строка2.Добавить(10);
Строка2.Добавить(12);
Строка2.Добавить(0);
Строка2.Добавить(0);
Емкость.Добавить(Строка2);
Строка3 = Новый Массив;
Строка3.Добавить(0);
Строка3.Добавить(4);
Строка3.Добавить(0);
Строка3.Добавить(0);
Строка3.Добавить(14);
Строка3.Добавить(0);
Емкость.Добавить(Строка3);
Строка4 = Новый Массив;
Строка4.Добавить(0);
Строка4.Добавить(0);
Строка4.Добавить(9);
Строка4.Добавить(0);
Строка4.Добавить(0);
Строка4.Добавить(20);
Емкость.Добавить(Строка4);
Строка5 = Новый Массив;
Строка5.Добавить(0);
Строка5.Добавить(0);
Строка5.Добавить(0);
Строка5.Добавить(7);
Строка5.Добавить(0);
Строка5.Добавить(4);
Емкость.Добавить(Строка5);
Строка6 = Новый Массив;
Строка6.Добавить(0);
Строка6.Добавить(0);
Строка6.Добавить(0);
Строка6.Добавить(0);
Строка6.Добавить(0);
Строка6.Добавить(0);
Емкость.Добавить(Строка6);
Источник = 0; // Индекс источника
Сток = 5; // Индекс стока
Поток = Новый Массив; // Матрица потоков (изначально все нули)
Для i = 0 По Емкость.Количество() - 1 Цикл
Поток.Добавить(Новый Массив);
Для j = 0 По Емкость.Количество() - 1 Цикл
Поток[i].Добавить(0);
КонецЦикла;
КонецЦикла;
МаксимальныйПоток = 0;
Пока Истина Цикл
// 1. Поиск увеличивающего пути с помощью BFS
УвеличивающийПуть = НайтиУвеличивающийПуть(Емкость, Поток, Источник, Сток);
Если УвеличивающийПуть = Неопределено Тогда
// Больше увеличивающих путей нет, завершаем
Прервать;
КонецЕсли;
// 2. Определение минимальной пропускной способности на пути
МинимальнаяПропускнаяСпособность = Бесконечность;
Для i = 0 По УвеличивающийПуть.Количество() - 2 Цикл
Откуда = УвеличивающийПуть[i];
Куда = УвеличивающийПуть[i + 1];
МинимальнаяПропускнаяСпособность = Мин(МинимальнаяПропускнаяСпособность, Емкость[Откуда][Куда] - Поток[Откуда][Куда]);
КонецЦикла;
// 3. Увеличение потока вдоль пути
Для i = 0 По УвеличивающийПуть.Количество() - 2 Цикл
Откуда = УвеличивающийПуть[i];
Куда = УвеличивающийПуть[i + 1];
Поток[Откуда][Куда] = Поток[Откуда][Куда] + МинимальнаяПропускнаяСпособность;
Поток[Куда][Откуда] = Поток[Куда][Откуда] - МинимальнаяПропускнаяСпособность; // Обратное направление для "отмены" потока
КонецЦикла;
МаксимальныйПоток = МаксимальныйПоток + МинимальнаяПропускнаяСпособность;
КонецЦикла;
Сообщить("Максимальный поток: " + МаксимальныйПоток);
// Вывод матрицы потоков (для отладки)
Для i = 0 По Емкость.Количество() - 1 Цикл
СтрокаВывода = "";
Для j = 0 По Емкость.Количество() - 1 Цикл
СтрокаВывода = СтрокаВывода + Строка(Поток[i][j]) + " ";
КонецЦикла;
Сообщить(СтрокаВывода);
КонецЦикла;
КонецПроцедуры
После завершения основного цикла, когда больше не остается увеличивающих путей, алгоритм Форда-Фалкерсона находит максимальный поток, который можно пропустить через транспортную сеть от источника к стоку. Результат работы алгоритма выводится в виде сообщения, содержащего значение максимального потока. В нашем коде это делается с помощью следующей строки:
Сообщить("Максимальный поток: " + МаксимальныйПоток);
Кроме того, для целей отладки и анализа работы алгоритма, мы также выводим матрицу потоков Поток. Эта матрица показывает, какое количество потока проходит по каждому ребру транспортной сети в конечном состоянии.
Пример вывода и его интерпретация:
Допустим, в результате работы алгоритма мы получили следующий вывод:
Максимальный поток: 23
0 12 11 0 0 0
-12 0 0 12 0 0
-11 0 0 0 11 0
0 -12 0 0 -7 19
0 0 -11 7 0 4
0 0 0 -19 -4 0
-
Максимальный поток: 23 - Это означает, что максимальное количество потока, которое можно пропустить через транспортную сеть от источника (узел 0) к стоку (узел 5), равно 23 единицам.
Матрица потоков: Каждая строка и столбец матрицы соответствует узлу транспортной сети. Значение Поток[i][j] показывает, какое количество потока проходит от узла i к узлу j. Отрицательное значение Поток[i][j] означает, что поток идет в обратном направлении, то есть от узла j к узлу i.
- Строка 0 (источник): 0 12 11 0 0 0 - Из источника (узел 0) 12 единиц потока идет к узлу 1, 11 единиц потока идет к узлу 2.
- Строка 1: -12 0 0 12 0 0 - 12 единиц потока идет от узла 1 к узлу 0 (обратное направление). 12 единиц потока идет от узла 1 к узлу 3.
- Строка 2: -11 0 0 0 11 0 - 11 единиц потока идет от узла 2 к узлу 0 (обратное направление). 11 единиц потока идет от узла 2 к узлу 4.
- Строка 3: 0 -12 0 0 -7 19 - 12 единиц потока идет от узла 3 к узлу 1 (обратное направление). 7 единиц потока идет от узла 3 к узлу 4 (обратное направление). 19 единиц потока идет от узла 3 к узлу 5 (стоку).
- Строка 4: 0 0 -11 7 0 4 - 11 единиц потока идет от узла 4 к узлу 2 (обратное направление). 7 единиц потока идет от узла 4 к узлу 3. 4 единицы потока идет от узла 4 к узлу 5 (стоку).
- Строка 5 (сток): 0 0 0 -19 -4 0 - В сток (узел 5) приходит 19 единиц потока от узла 3 и 4 единицы потока от узла 4.
Анализируя матрицу потоков, можно понять, как именно распределяется поток по транспортной сети и какие ребра являются наиболее загруженными.
Реализация алгоритма Форда-Фалкерсона в среде 1С, как и любой другой алгоритм, имеет свои особенности и ограничения, которые необходимо учитывать при его применении в реальных задачах. Производительность: Одним из основных ограничений является производительность. 1С не является платформой, предназначенной для выполнения сложных математических вычислений. Алгоритм Форда-Фалкерсона, особенно при использовании BFS для поиска увеличивающих путей, может потребовать значительных вычислительных ресурсов, особенно для графов с большим количеством узлов и ребер. Это может привести к тому, что время выполнения алгоритма станет неприемлемо большим, особенно при работе с большими объемами данных. Представление графа: Выбор способа представления графа также влияет на производительность. Мы использовали матрицу смежности, которая удобна для небольших графов, но требует много памяти для больших и разреженных графов. Альтернативой могут быть списки смежности, но это усложняет реализацию и требует дополнительных усилий по оптимизации доступа к данным. Применимость: Алгоритм Форда-Фалкерсона, как мы уже отмечали, подходит только для задач, которые можно упростить и представить в виде транспортной сети. При моделировании реальных бизнес-процессов с использованием алгоритма Форда-Фалкерсона необходимо тщательно проанализировать задачу и убедиться, что упрощенная модель достаточно адекватно отражает реальность. Альтернативные подходы: Для решения более сложных задач оптимизации в 1С можно использовать альтернативные подходы, такие как: Внешние компоненты: Использование внешних компонент, написанных на других языках программирования (например, C++ или Java), которые более эффективно выполняют математические вычисления. Специализированные библиотеки: Использование специализированных библиотек оптимизации, которые предоставляют готовые алгоритмы и функции для решения различных задач. Эвристические алгоритмы: Использование эвристических алгоритмов, которые не гарантируют нахождение оптимального решения, но могут быстро найти достаточно хорошее решение для сложных задач. В заключение, реализация алгоритма Форда-Фалкерсона в 1С требует тщательного рассмотрения ограничений платформы и всестороннего анализа решаемой задачи. Хотя он может быть полезен для определенных упрощенных сценариев, важно осознавать его ограничения и рассматривать альтернативные подходы для более сложных задач оптимизации.
Визуализация результатов работы алгоритма Форда-Фалкерсона может значительно упростить анализ и понимание полученных данных. Хотя 1С не обладает развитыми средствами визуализации, существуют различные способы представления результатов, которые могут быть полезны для пользователей.
Одним из самых простых способов является представление матрицы потоков в виде таблицы. Это позволяет увидеть, какое количество потока проходит по каждому ребру графа. Однако, для больших графов такая таблица может быть сложной для восприятия.
Более наглядным способом является использование диаграмм. Например, можно построить столбчатую диаграмму, показывающую количество потока, входящего и выходящего из каждого узла. Это позволяет быстро выявить узлы, которые являются основными потребителями или поставщиками потока.
Для визуализации транспортной сети можно использовать графические схемы. На такой схеме узлы представляются в виде кругов или прямоугольников, а ребра - в виде стрелок. Толщина стрелок может соответствовать величине потока, проходящего по данному ребру. Это позволяет наглядно увидеть распределение потока по сети и выявить "узкие места", которые ограничивают пропускную способность.
Примеры визуализации:
- Таблица: Отображение матрицы "Поток" в виде таблицы, где строки и столбцы соответствуют узлам графа, а значения ячеек - величине потока между узлами.
- Диаграмма: Столбчатая диаграмма, показывающая входящий и исходящий поток для каждого узла.
- Графическая схема: Схема транспортной сети с узлами и ребрами, где толщина ребер пропорциональна величине потока.
- Для реализации визуализации в 1С можно использовать различные инструменты, такие как:
- Табличный документ: Для отображения табличных данных.
- Диаграмма: Для построения различных типов диаграмм.
- Схема: Для создания графических схем.
Выбор способа визуализации зависит от конкретной задачи и требований пользователя. Важно, чтобы визуализация была понятной, наглядной и помогала пользователю принимать обоснованные решения на основе полученных данных.
Данная статья предназначена для следующих категорий пользователей 1С:
- Программисты 1С: Разработчики, занимающиеся решением задач оптимизации и распределения ресурсов в среде 1С. Статья будет полезна тем, кто ищет способы применения математических алгоритмов, таких как алгоритм Форда-Фалкерсона, для решения реальных бизнес-задач.
- Консультанты 1С: Специалисты, занимающиеся внедрением и настройкой системы 1С для клиентов. Статья поможет консультантам понять, как можно использовать алгоритм Форда-Фалкерсона для оптимизации логистических процессов, управления запасами и распределения задач между сотрудниками.
- Аналитики 1С: Специалисты, занимающиеся анализом данных и разработкой отчетов в системе 1С. Статья предоставит аналитикам информацию о том, как можно использовать алгоритм Форда-Фалкерсона для выявления узких мест в бизнес-процессах и повышения эффективности использования ресурсов.
- Студенты и начинающие специалисты 1С: Статья может быть полезна студентам и начинающим специалистам, которые изучают программирование в среде 1С и интересуются применением математических алгоритмов для решения практических задач.
Статья предполагает, что читатель обладает базовыми знаниями программирования в среде 1С и понимает основные принципы работы с массивами, циклами и функциями. Также желательно знакомство с основами теории графов и алгоритмов.
Основная цель статьи - показать, как можно адаптировать алгоритм Форда-Фалкерсона для использования в среде 1С, учитывая ее ограничения и особенности. Статья содержит примеры кода и подробные объяснения, которые помогут читателям самостоятельно реализовать алгоритм и использовать его для решения своих задач.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.16.97
Вступайте в нашу телеграмм-группу Инфостарт