Расчет финансовых показателей в 1С 8.3: Сложные проценты, аннуитеты и модель Блэка-Шоулза

Расчет финансовых показателей в 1С 8.3: Сложные проценты, аннуитеты и модель Блэка-Шоулза

Финансовые расчеты являются неотъемлемой частью автоматизации бизнес-процессов на предприятиях любого масштаба. От точного расчета сложных процентов по кредитам до оценки стоимости сложных финансовых инструментов, таких как опционы, зависит принятие обоснованных инвестиционных и управленческих решений. Платформа 1С:Предприятие 8.3, благодаря своей гибкости и широким возможностям, позволяет реализовать широкий спектр финансовых расчетов и моделей.

Однако, для эффективного использования платформы 1С в финансовых расчетах необходимо учитывать ряд особенностей и ограничений. В частности, отсутствие встроенных математических функций, таких как натуральный логарифм и квадратный корень, требует использования альтернативных подходов. Кроме того, для реализации более сложных финансовых моделей, таких как модель Блэка-Шоулза, необходимо уметь адаптировать численные методы и алгоритмы для работы в среде 1С.

В данной статье мы рассмотрим реализацию расчета сложных процентов, аннуитетных платежей и модели Блэка-Шоулза для оценки стоимости опционов в 1С 8.3.

2. Расчет сложных процентов и аннуитетов в 1С

В данном разделе мы рассмотрим реализацию двух базовых финансовых расчетов: сложных процентов и аннуитетных платежей. Эти расчеты широко используются в задачах кредитования, инвестирования и финансового планирования.

2.1. Сложные проценты

Сложные проценты представляют собой способ начисления процентов, при котором процент за каждый период начисляется не только на основную сумму, но и на ранее начисленные проценты. Формула расчета сложных процентов выглядит следующим образом:

FV = PV * (1 + r)^n

Где:

• FV - будущая стоимость (Future Value)
• PV- текущая стоимость (Present Value) или начальный капитал
• r- процентная ставка за период (в долях единицы)
• n - количество периодов

Пример применения: Расчет будущей стоимости инвестиции.

Предположим, мы инвестируем 10 000 рублей под 10% годовых на 5 лет. Какова будет будущая стоимость инвестиции?

PV = 10000
r = 0.10
n = 5
FV = 10000 * (1 + 0.10)^5 = 16105.10 рублей

2.2. Аннуитетные платежи

Аннуитет - это серия равных платежей, производимых через равные промежутки времени. Аннуитетные платежи часто используются при погашении кредитов и займов. Формула расчета аннуитетного платежа выглядит следующим образом:

PMT = PV * (r * (1 + r)^n) / ((1 + r)^n - 1)

Где:

• PMT - аннуитетный платеж (Payment)
• PV - текущая стоимость (Present Value) или сумма кредита
• r - процентная ставка за период (в долях единицы)
• n - количество периодов

Пример применения: Расчет ежемесячного платежа по кредиту.

Предположим, мы берем кредит в размере 500 000 рублей под 12% годовых (1% в месяц) на 5 лет (60 месяцев). Каков будет ежемесячный платеж?

PV = 500000
r = 0.01
n = 60
PMT = 500000 * (0.01 * (1 + 0.01)^60) / ((1 + 0.01)^60 - 1) = 11122.24 рублей

2.3. Реализация в 1С

Для реализации расчетов сложных процентов и аннуитетных платежей в 1С можно использовать следующие фрагменты кода:

&НаКлиенте
Процедура РассчитатьНажатие(Команда)

    // **Формирование строки с начальными данными**
    НачальныеДанныеСтрока = "";

    // **Расчет сложных процентов**
    НачальныйКапитал = 10000;       // Начальная сумма
    ПроцентнаяСтавка = 0.10;        // Годовая процентная ставка (10%)
    КоличествоПериодов = 5;        // Количество лет

    НачальныеДанныеСтрока = НачальныеДанныеСтрока + "Начальный капитал: " + Строка(НачальныйКапитал) + Символы.ПС;
    НачальныеДанныеСтрока = НачальныеДанныеСтрока + "Процентная ставка: " + Строка(ПроцентнаяСтавка) + Символы.ПС;
    НачальныеДанныеСтрока = НачальныеДанныеСтрока + "Количество периодов: " + Строка(КоличествоПериодов) + Символы.ПС;
    НачальныеДанныеСтрока = НачальныеДанныеСтрока + Символы.ПС; // Разделитель

    // **Расчет аннуитета (пример)**
    СуммаКредита = 500000;
    ПроцентнаяСтавкаМесячная = 0.01; // 1% в месяц
    СрокКредитаВМесяцах = 60;

    НачальныеДанныеСтрока = НачальныеДанныеСтрока + "Сумма кредита: " + Строка(СуммаКредита) + Символы.ПС;
    НачальныеДанныеСтрока = НачальныеДанныеСтрока + "Процентная ставка месячная: " + Строка(ПроцентнаяСтавкаМесячная) + Символы.ПС;
    НачальныеДанныеСтрока = НачальныеДанныеСтрока + "Срок кредита в месяцах: " + Строка(СрокКредитаВМесяцах) + Символы.ПС;
    НачальныеДанныеСтрока = НачальныеДанныеСтрока + Символы.ПС; // Разделитель

    // **Оценка стоимости опциона (модель Блэка-Шоулза)**
    ЦенаАкции = 100;
    ЦенаИсполнения = 110;
    ВремяДоИсполнения = 1;      // 1 год
    БезрисковаяСтавка = 0.05;
    Волатильность = 0.20;

    НачальныеДанныеСтрока = НачальныеДанныеСтрока + "Цена акции: " + Строка(ЦенаАкции) + Символы.ПС;
    НачальныеДанныеСтрока = НачальныеДанныеСтрока + "Цена исполнения: " + Строка(ЦенаИсполнения) + Символы.ПС;
    НачальныеДанныеСтрока = НачальныеДанныеСтрока + "Время до исполнения: " + Строка(ВремяДоИсполнения) + Символы.ПС;
    НачальныеДанныеСтрока = НачальныеДанныеСтрока + "Безрисковая ставка: " + Строка(БезрисковаяСтавка) + Символы.ПС;
    НачальныеДанныеСтрока = НачальныеДанныеСтрока + "Волатильность: " + Строка(Волатильность) + Символы.ПС;
    НачальныеДанныеСтрока = НачальныеДанныеСтрока + Символы.ПС; // Разделитель

    // **Вывод начальных данных в реквизит формы**
    Объект.НачальныеДанные = НачальныеДанныеСтрока;

    // **Вычисления на сервере**
    Результаты = РассчитатьНаСервере(ЦенаАкции, ЦенаИсполнения, ВремяДоИсполнения, БезрисковаяСтавка, Волатильность);

    // **Вывод результатов в реквизит формы**
    Объект.РезультатМодели = Результаты;

КонецПроцедуры

Функция Pow(x, y) используется для возведения числа x в степень y.

Функция Формат(Число, СтрокаФормата) используется для форматирования числового значения при выводе (два знака после запятой, разделитель - точка).

Описание функции НормальноеРаспределение(X):

&НаСервере
Функция НормальноеРаспределение(X)

    // Аппроксимация кумулятивной функции нормального распределения
    // по методу Абтрамовица и Стигуна.

    Если X >= 0 Тогда
        T = 1 / (1 + 0.2316419 * X);
        Результат = 1 - 0.3989423 * Exp(-X * X / 2) * (0.3193815 * T - 0.3565638 * Pow(T, 2) + 1.781478 * Pow(T, 3) - 1.821256 * Pow(T, 4) + 1.330274 * Pow(T, 5));
    Иначе
        Результат = 1 - НормальноеРаспределение(-X);
    КонецЕсли;

    Возврат Результат;

КонецФункции

Функция предназначена для аппроксимации значения кумулятивной функции стандартного нормального распределения (cumulative distribution function, CDF) для заданного значения аргумента X. Кумулятивная функция нормального распределения возвращает вероятность того, что случайная величина, имеющая стандартное нормальное распределение, примет значение, меньшее или равное X.

Параметры:

• X (Число) - Значение аргумента, для которого необходимо вычислить кумулятивную функцию нормального распределения.

Возвращаемое значение:

• (Число) - Приблизительное значение кумулятивной функции стандартного нормального распределения для аргумента X. Значение находится в диапазоне от 0 до 1.

Реализация:

Функция использует метод аппроксимации Абтрамовица и Стигуна (Abramowitz and Stegun), который представляет собой полиномиальную аппроксимацию кумулятивной функции нормального распределения. Этот метод обеспечивает достаточно высокую точность при относительно простой реализации.

Алгоритм:

1. Обработка отрицательных значений: Если аргумент X отрицательный, функция рекурсивно вызывает себя с аргументом -X и возвращает 1 - НормальноеРаспределение(-X). Это использует свойство симметрии стандартного нормального распределения.
2. Расчет вспомогательной переменной T: Вычисляется вспомогательная переменная T по формуле T = 1 / (1 + 0.2316419 * X).
3. Полиномиальная аппроксимация: Вычисляется аппроксимация кумулятивной функции нормального распределения с использованием полинома от T и констант, взятых из метода Абтрамовица и Стигуна.
4. Возврат результата: Функция возвращает вычисленное приближенное значение кумулятивной функции нормального распределения.

Метод аппроксимации имеет определенную погрешность. Если требуется высокая точность, рекомендуется использовать внешнюю компоненту или другой, более точный метод.

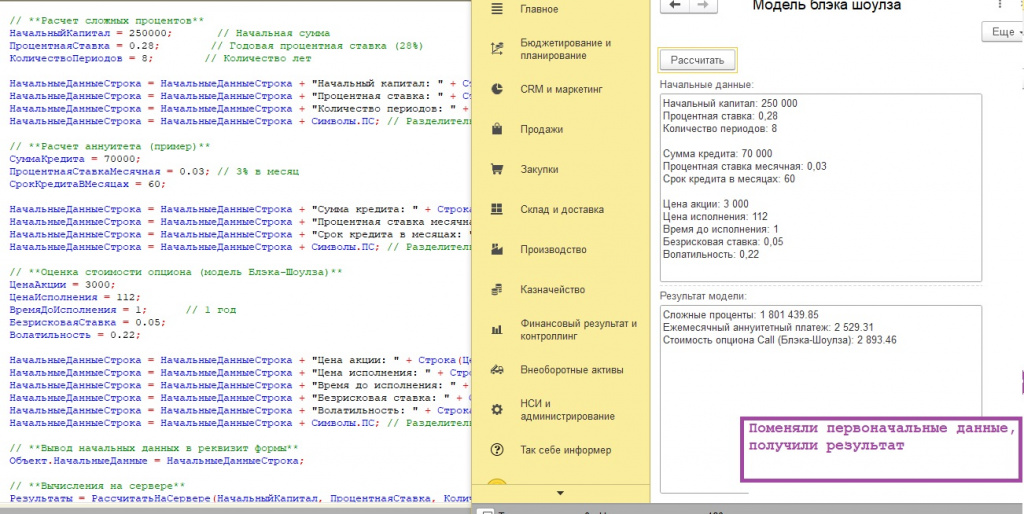
Код 1с мы применили, и посмотрим на результат (выполнение алгоритма см.скриншоты).

Входные данные для расчетов включают в себя параметры, необходимые для вычисления сложных процентов, аннуитетных платежей и стоимости опциона Call по модели Блэка-Шоулза.

1. Расчет сложных процентов:

• Начальный капитал: 10 000 рублей - сумма, которая инвестируется или кладется на счет в начале периода.
• Процентная ставка: 0,1 (10%) - годовая процентная ставка, используемая для начисления процентов. Выражается в долях единицы.
• Количество периодов: 5 лет - срок, на который инвестируется капитал или начисляются проценты.

2. Расчет аннуитетных платежей:

• Сумма кредита: 500 000 рублей - общая сумма кредита, которую необходимо выплатить.
• Процентная ставка месячная: 0,01 (1%) - месячная процентная ставка по кредиту. Выражается в долях единицы.
• Срок кредита в месяцах: 60 месяцев - срок, в течение которого необходимо погасить кредит.

3. Оценка стоимости опциона Call (модель Блэка-Шоулза):

• Цена акции: 100 рублей - текущая рыночная цена базовой акции, на которую выпущен опцион.
• Цена исполнения: 110 рублей - цена, по которой владелец опциона имеет право купить акцию в будущем.
• Время до исполнения: 1 год - срок, оставшийся до даты истечения опциона (экспирации). Выражается в годах.
• Безрисковая ставка: 0,05 (5%) - процентная ставка по безрисковому активу, например, государственным облигациям, с аналогичным сроком погашения, что и опцион. Выражается в долях единицы.
• Волатильность: 0,2 (20%) - мера изменчивости цены акции. Выражается как стандартное отклонение доходности акции в год.

Результаты выполнения:

После выполнения расчетов с использованием указанных входных данных были получены следующие результаты:

• Сложные проценты: 16 105.10 рублей - будущая стоимость инвестиции в размере 10 000 рублей под 10% годовых на 5 лет.
• Ежемесячный аннуитетный платеж: 11 122.22 рублей - сумма ежемесячного платежа, необходимая для погашения кредита в размере 500 000 рублей под 1% в месяц на 60 месяцев.
• Стоимость опциона Call (Блэка-Шоулза): 6.04 рублей - теоретическая стоимость опциона Call, рассчитанная по модели Блэка-Шоулза с использованием заданных входных параметров.

Эти результаты демонстрируют работу реализованных алгоритмов и позволяют оценить их применимость для решения различных финансовых задач. Важно отметить, что модель Блэка-Шоулза имеет ряд ограничений и предполагает определенные допущения, поэтому полученная стоимость опциона является лишь приблизительной оценкой.

В данной статье мы рассмотрели реализацию расчета сложных процентов, аннуитетных платежей и модели Блэка-Шоулза для оценки стоимости опционов в среде 1С 8.3. Мы показали, как адаптировать математические формулы и алгоритмы для работы на платформе 1С, учитывая ее особенности и ограничения.

Реализация финансовых расчетов в 1С позволяет автоматизировать рутинные операции, повысить точность вычислений и интегрировать их в существующие бизнес-процессы предприятия. Рассмотренные примеры демонстрируют возможность использования 1С для решения широкого круга задач, связанных с финансовым анализом и моделированием.

В то же время, важно помнить об ограничениях платформы 1С. Отсутствие встроенных математических функций требует использования альтернативных подходов, таких как реализация собственных функций (например, Sqrt и аппроксимация кумулятивнойлями системы 1С.

Рекомендации:

• Тщательно тестируйте реализованные финансовые расчеты и модели.
• Сравнивайте результаты с другими инструментами и источниками данных.
• Учитывайте ограничения платформы 1С и выбирайте оптимальные подходы для решения конкретных задач.
• Изучайте новые возможности платформы 1С и используйте их для улучшения и расширения функциональности финансовых расчетов.

Надеемся, что данная статья будет полезна программистам, консультантам и финансовым аналитикам, использующим 1С для автоматизации финансовых расчетов и моделирования.