В современном бизнесе все больные решения для малых и средних предприятий. В таких случаях возникает необходимость использования имеющихся инструментов, таких как 1С:Предприятие 8.3.
Платформа 1С широко используется для автоматизации бизнес-процессов, и, несмотря на ее специализацию, она предоставляет возможности для реализации базовых алгоритмов машинного обучения. В частности, алгоритм K-ближайших соседей (KNN), благодаря своей простоте и интуитивности, может быть успешно реализован в 1С для решения задач классификации.
Алгоритм K-ближайших соседей (KNN) — это простой и интуитивно понятный алгоритм машинного обучения, который используется для задач классификации и регрессии. В основе KNN лежит принцип "похожее на похожее". Алгоритм предполагает, что новые данные будут классифицированы на основе близости к имеющимся данным.
Математические основы:
-
Пространство признаков (Feature Space): Каждый объект (запись данных) представляется точкой в многомерном пространстве, где каждая размерность соответствует признаку (переменной). Например, если у нас есть объекты, описываемые двумя признаками (рост и вес), то каждый объект будет точкой на плоскости.
-
Метрика расстояния (Distance Metric): Ключевым элементом KNN является метрика расстояния, которая определяет, насколько "близки" друг к другу два объекта в пространстве признаков. Наиболее распространенной метрикой является Евклидово расстояние (Euclidean Distance):
d(x, y) = √( Σ (xi - yi)2 )
где:
- x и y – два объекта (точки в пространстве признаков).
- xi и yi – значения i-го признака для объектов x и y соответственно.
- Σ – сумма по всем признакам.
Другие метрики расстояния:
-
Манхэттенское расстояние (Manhattan Distance): Сумма абсолютных разностей между значениями признаков. d(x, y) = Σ |xi - yi|
-
Расстояние Чебышева (Chebyshev Distance): Максимальная разница по любому из признаков. d(x, y) = max(|xi - yi|)
Выбор метрики расстояния зависит от типа данных и специфики задачи.
-
Параметр K (Number of Neighbors): Это гиперпараметр, который определяет, сколько ближайших соседей будут учитываться при классификации. Выбор оптимального значения K – важная задача, которая влияет на производительность алгоритма.
-
Классификация:
- Для задачи классификации: Алгоритм KNN определяет класс нового объекта путем “голосования” среди K ближайших соседей. Класс, который чаще всего встречается среди K соседей, присваивается новому объекту.
- Если k=1, то класс присваивается ближайшему соседу.
- Если k=3, то алгоритм выбирает 3 ближайших соседа и присваивает классу объекта класс, который чаще всего встречается среди этих трёх.
- Для задачи регрессии: Предсказанное значение – это среднее значение целевой переменной (например, цены) среди K ближайших соседей.
- Для задачи классификации: Алгоритм KNN определяет класс нового объекта путем “голосования” среди K ближайших соседей. Класс, который чаще всего встречается среди K соседей, присваивается новому объекту.
-
Алгоритм работы:
- Обучение (Training): Алгоритм KNN не требует обучения в явном виде. Просто хранятся данные обучающей выборки.
- Классификация нового объекта:
- Вычисляется расстояние от нового объекта до каждого объекта в обучающей выборке.
- На основе выбранной метрики расстояния выбираются K ближайших соседей.
- Определяется класс нового объекта на основе большинства классов среди K соседей (для классификации) или вычисляется среднее значение целевой переменной (для регрессии).
Преимущества KNN:
- Простота реализации: Легко понять и реализовать.
- Отсутствие этапа обучения: Нет необходимости в обучении модели.
- Гибкость: Может использоваться как для классификации, так и для регрессии.
Недостатки KNN:
- Высокая вычислительная сложность: Вычисление расстояний до всех объектов обучающей выборки может быть ресурсоемким, особенно для больших наборов данных.
- Чувствительность к масштабу признаков: Признаки с большим диапазоном значений могут доминировать над признаками с меньшим диапазоном. Необходима нормализация данных.
- Выбор K: Оптимальное значение K не всегда очевидно и требует настройки.
- Проблемы с несбалансированными классами: Алгоритм может быть предвзятым по отношению к классам с большим количеством представителей.
Значимость и применение KNN в 1С:
Несмотря на то, что 1С не является платформой для углубленного машинного обучения, реализация KNN может быть полезна в следующих сценариях:
- Простая классификация данных: KNN может быть использован для классификации клиентов по группам, определения категорий товаров, выявления подозрительных операций и других задач, где требуется отнесение объектов к определенному классу на основе их признаков.
- Быстрая прототипизация: KNN легко реализовать и настроить, что позволяет быстро создать прототип решения и оценить его применимость для конкретной задачи.
- Обучение и демонстрация: KNN является отличным алгоритмом для изучения основ машинного обучения и демонстрации принципов классификации данных.
- Интеграция с бизнес-процессами: KNN, реализованный в 1С, может быть легко интегрирован в существующие бизнес-процессы предприятия, что позволяет автоматизировать принятие решений на основе анализа данных.
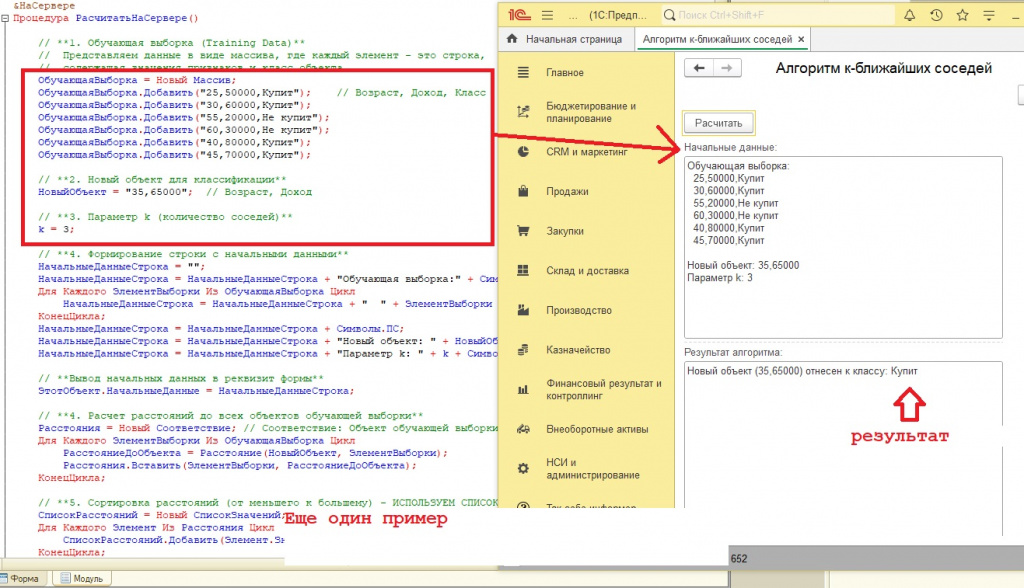
Применение на практике (с использованием кода):
В данном разделе мы рассмотрим практическую реализацию алгоритма KNN в 1С 8.3 без использования реквизитов формы. Это позволит нам сосредоточиться на основных принципах работы алгоритма и упростить его понимание.
&НаСервере
Процедура РасчитатьНаСервере()
// **1. Обучающая выборка**
// Представляем данные в виде массива, где каждый элемент - это строка,
// содержащая значения признаков и класс объекта.
ОбучающаяВыборка = Новый Массив;
ОбучающаяВыборка.Добавить("1,2,Красный"); // Признак1, Признак2, Класс
ОбучающаяВыборка.Добавить("2,1,Красный");
ОбучающаяВыборка.Добавить("5,6,Синий");
ОбучающаяВыборка.Добавить("6,5,Синий");
ОбучающаяВыборка.Добавить("7,8,Зеленый");
ОбучающаяВыборка.Добавить("8,7,Зеленый");
// **2. Новый объект для классификации**
НовыйОбъект = "3,3"; // Признак1, Признак2
// **3. Параметр k (количество соседей)**
k = 3;
// **4. Формирование строки с начальными данными**
НачальныеДанныеСтрока = "";
НачальныеДанныеСтрока = НачальныеДанныеСтрока + "Обучающая выборка:" + Символы.ПС;
Для Каждого ЭлементВыборки Из ОбучающаяВыборка Цикл
НачальныеДанныеСтрока = НачальныеДанныеСтрока + " " + ЭлементВыборки + Символы.ПС;
КонецЦикла;
НачальныеДанныеСтрока = НачальныеДанныеСтрока + Символы.ПС;
НачальныеДанныеСтрока = НачальныеДанныеСтрока + "Новый объект: " + НовыйОбъект + Символы.ПС;
НачальныеДанныеСтрока = НачальныеДанныеСтрока + "Параметр k: " + k + Символы.ПС;
// **Вывод начальных данных в реквизит формы**
ЭтотОбъект.НачальныеДанные = НачальныеДанныеСтрока;
// **4. Расчет расстояний до всех объектов обучающей выборки**
Расстояния = Новый Соответствие; // Соответствие: Объект обучающей выборки -> Расстояние
Для Каждого ЭлементВыборки Из ОбучающаяВыборка Цикл
РасстояниеДоОбъекта = Расстояние(НовыйОбъект, ЭлементВыборки);
Расстояния.Вставить(ЭлементВыборки, РасстояниеДоОбъекта);
КонецЦикла;
// **5. Сортировка расстояний (от меньшего к большему) - ИСПОЛЬЗУЕМ СПИСОК ЗНАЧЕНИЙ**
СписокРасстояний = Новый СписокЗначений;
Для Каждого Элемент Из Расстояния Цикл
СписокРасстояний.Добавить(Элемент.Значение, Элемент.Ключ); // Значение (расстояние) - ключ для сортировки
КонецЦикла;
СписокРасстояний.СортироватьПоЗначению(НаправлениеСортировки.Возр);
// **6. Выбор k ближайших соседей**
БлижайшиеСоседи = Новый Массив;
Для Индекс = 0 По k - 1 Цикл
БлижайшиеСоседи.Добавить(СписокРасстояний[Индекс].Представление); // Представление - это наш объект обучающей выборки
КонецЦикла;
// **7. Определение класса нового объекта (голосование)**
СчетчикКлассов = Новый Соответствие; // Соответствие: Класс -> Количество голосов
Для Каждого Сосед Из БлижайшиеСоседи Цикл
МассивСоседа = СтрРазделить(Сосед, ",", Ложь);
КлассСоседа = МассивСоседа[2]; // Класс находится в третьем элементе строки
КоличествоГолосов = СчетчикКлассов.Получить(КлассСоседа);
Если КоличествоГолосов = Неопределено Тогда
СчетчикКлассов.Вставить(КлассСоседа, 1);
Иначе
СчетчикКлассов[КлассСоседа] = КоличествоГолосов + 1;
КонецЕсли;
КонецЦикла;
// **8. Определение класса с наибольшим количеством голосов**
НаиболееВероятныйКласс = "";
МаксимальноеКоличествоГолосов = 0;
Для Каждого ЭлементСчетчика Из СчетчикКлассов Цикл
Если ЭлементСчетчика.Значение > МаксимальноеКоличествоГолосов Тогда
НаиболееВероятныйКласс = ЭлементСчетчика.Ключ;
МаксимальноеКоличествоГолосов = ЭлементСчетчика.Значение;
КонецЕсли;
КонецЦикла;
// **9. Формирование строки с результатом**
РезультатАлгоритмаСтрока = "Новый объект (" + НовыйОбъект + ") отнесен к классу: " + НаиболееВероятныйКласс;
// **Вывод результата в реквизит формы**
ЭтотОбъект.РезультатАлгоритма = РезультатАлгоритмаСтрока;
КонецПроцедуры
Описание кода:
- Обучающая выборка: Задаются данные для обучения алгоритма. Каждый объект представлен строкой в формате "Признак1,Признак2,Класс".
- Новый объект: Объект, который необходимо классифицировать.
- Параметр K: Определяет количество ближайших соседей, участвующих в голосовании.
- Функция Расстояние: Вычисляет Евклидово расстояние между двумя объектами.
- Расчет расстояний: Вычисляются расстояния от нового объекта до всех объектов обучающей выборки и сохраняются в Соответствие.
- Сортировка расстояний: Расстояния сортируются по возрастанию с использованием СпискаЗначений.
- Выбор K ближайших соседей: Выбираются K объектов с наименьшими расстояниями.
- Определение класса: Класс нового объекта определяется голосованием среди K ближайших соседей. Класс, получивший наибольшее количество голосов, считается наиболее вероятным.
- Вывод результатов: Результаты выводятся в строковые реквизиты формы "НачальныеДанные" и "РезультатАлгоритма".
Дополнительные процедуры и функции:
&НаСервере
Функция Расстояние(Объект1, Объект2)
Массив1 = СтрРазделить(Объект1, ",", Ложь);
Массив2 = СтрРазделить(Объект2, ",", Ложь);
Признак1_1 = Число(Массив1[0]);
Признак1_2 = Число(Массив1[1]);
Признак2_1 = Число(Массив2[0]);
Признак2_2 = Число(Массив2[1]);
Результат = SSqrt(Pow((Признак1_1 - Признак2_1), 2) + Pow((Признак1_2 - Признак2_2), 2));
Возврат Результат;
КонецФункции
&НаСервере
Функция SSqrt(Значение)
Возврат Pow(Значение, 0.5);
КонецФункции
Выбор правильной метрики расстояния является критически важным шагом в применении алгоритма K-ближайших соседей (KNN). Метрика определяет, как алгоритм измеряет близость между объектами в пространстве признаков, и, следовательно, напрямую влияет на результаты классификации. Неправильный выбор метрики может привести к неточным результатам и снижению производительности алгоритма.
Рассмотрим наиболее распространенные метрики расстояния и их особенности:
-
Евклидово расстояние (Euclidean Distance):
- Описание: Как мы уже говорили, это наиболее распространенная метрика, которая вычисляет прямолинейное расстояние между двумя точками в евклидовом пространстве. Она измеряет “расстояние по прямой” между объектами.
- Формула: d(x, y) = √( Σ (xi - yi)2 )
- Применение: Подходит для данных, где признаки имеют одинаковый масштаб и распределены примерно нормально. Хорошо работает с непрерывными числовыми признаками.
- Влияние на результаты: Если признаки имеют разные масштабы, Евклидово расстояние может быть искажено, так как признаки с большими значениями будут вносить больший вклад в расчет расстояния. Необходимо масштабирование данных.
-
Манхэттенское расстояние (Manhattan Distance) / L1-норма:
- Описание: Вычисляет расстояние между точками, измеряя сумму абсолютных разностей между координатами точек вдоль осей. Можно представить как путь по сетке улиц города.
- Формула: d(x, y) = Σ |xi - yi|
- Применение: Может быть более устойчивой к выбросам (outliers) в данных, чем Евклидово расстояние, поскольку не возводит разницу в квадрат. Часто используется, когда признаки представляют собой различные категории или ранги.
- Влияние на результаты: Меньше чувствительно к выбросам, но может быть менее точным, чем Евклидово расстояние, если данные имеют сложную структуру.
-
Расстояние Чебышева (Chebyshev Distance) / L∞-норма:
- Описание: Определяет расстояние как максимальную разницу между значениями по любой из размерностей. Рассматривает только самое большое отклонение по любому из признаков.
- Формула: d(x, y) = max(|xi - yi|)
- Применение: Полезно, когда важны выбросы, или когда необходимо минимизировать максимальное отклонение по какому-либо признаку. Пример: для хранения предметов в контейнере, где важна длина самого длинного предмета.
- Влияние на результаты: Чрезвычайно чувствительно к выбросам и может не подходить для большинства задач классификации.
-
Расстояние Минковского (Minkowski Distance):
- Описание: Общее обобщение Евклидова, Манхэттенского и Чебышевского расстояний.
- Формула: d(x, y) = (Σ |xi - yi|p)1/p, где p - параметр, определяющий порядок нормы.
- При p = 1, это Манхэттенское расстояние.
- При p = 2, это Евклидово расстояние.
- При p → ∞, это Чебышевское расстояние.
- Применение: Позволяет гибко выбирать метрику, настраивая параметр p.
- Влияние на результаты: Требует подбора параметра p, который зависит от структуры данных.
-
Расстояние Махаланобиса (Mahalanobis Distance):
- Описание: Учитывает ковариацию между признаками. Нормализует данные с учетом их распределения. Учитывает корреляцию между признаками.
- Формула: d(x, y) = √((x - y)T S-1 (x - y)) где S-1 - обратная ковариационная матрица.
- Применение: Подходит для данных с разными масштабами и ковариацией между признаками. Эффективна при наличии корреляции между признаками и для выявления выбросов.
- Влияние на результаты: Обеспечивает более точную классификацию, чем Евклидово расстояние, когда признаки коррелированы.
-
Косинусное расстояние (Cosine Distance):
- Описание: Измеряет косинус угла между двумя векторами. Оценивает сходство по направлению векторов, игнорируя их величину. Используется, когда важна ориентация, а не абсолютные значения признаков.
- Формула: cos θ = (x · y) / (||x|| ||y||) где:
- x · y – скалярное произведение векторов x и y.
- ||x|| и ||y|| – нормы (длины) векторов x и y.
- Применение: Часто используется в анализе текста, рекомендательных системах и обработке изображений.
- Влияние на результаты: Нечувствительно к масштабу данных. Может быть полезно, когда важна относительная частота признаков, а не их абсолютные значения.
Как выбрать подходящую метрику:
- Тип данных:
- Для непрерывных числовых признаков (с одинаковым масштабом): Евклидово расстояние, возможно, Манхэттенское.
- Для признаков с разным масштабом: Евклидово расстояние после нормализации (например, масштабирование к единичному интервалу или стандартизация). Расстояние Махаланобиса.
- Для категориальных признаков: Необходимо использовать специфические метрики для категориальных данных (например, расстояние Хэмминга, если категории закодированы в бинарном виде).
- Для данных с коррелированными признаками: Расстояние Махаланобиса.
- Для текста или данных, где важна ориентация: Косинусное расстояние.
- Предварительный анализ данных (EDA): Визуализация данных и изучение распределения признаков поможет определить подходящую метрику.
- Эксперименты: Попробуйте разные метрики и оцените качество классификации (например, с использованием перекрестной проверки).
- Знание предметной области: Учитывайте особенности предметной области, которые могут влиять на выбор метрики.
Важно:
- Нормализация данных (Data Scaling): Если признаки имеют разные диапазоны значений, необходимо выполнить масштабирование данных (например, стандартизацию или масштабирование к единичному интервалу) перед использованием Евклидова, Манхэттенского или других метрик, чувствительных к масштабу.
- Перекрестная проверка (Cross-Validation): Используйте перекрестную проверку для оценки производительности алгоритма с разными метриками.
- Подбор параметров: Помните, что выбор метрики часто связан с необходимостью подбора других параметров, таких как K, а также с предобработкой данных.
Выбор метрики расстояния — это важный этап, который требует понимания свойств ваших данных и того, как разные метрики измеряют сходство между объектами. В большинстве случаев, необходимо экспериментировать с разными метриками, чтобы найти ту, которая обеспечивает наилучшую производительность для вашей задачи.
Рассмотрение способов выбора оптимального значения K:
Выбор оптимального значения K (количества ближайших соседей) является ключевым для достижения высокой точности классификации в алгоритме K-ближайших соседей (KNN). Слишком маленькое значение K может привести к переобучению (overfitting), когда модель слишком сильно адаптируется к шуму в обучающей выборке и плохо обобщает на новые данные. Слишком большое значение K может привести к недообучению (underfitting), когда модель становится слишком простой и неспособной уловить сложные закономерности в данных.
Вот несколько способов выбора оптимального значения K:
-
Метод перекрестной проверки (Cross-Validation):
Разделили данные на 5 частей.
Итерация 1: обучаемся на частях 2,3,4,5; проверяем на части 1. Итерация 2: обучаемся на частях 1,3,4,5; проверяем на части 2. Итерация 3: обучаемся на частях 1,2,4,5; проверяем на части 3. Итерация 4: обучаемся на частях 1,2,3,5; проверяем на части 4. Итерация 5: обучаемся на частях 1,2,3,4; проверяем на части 5.Затем, усредняем результаты по всем 5 итерациям.
-
Описание: Это один из самых надежных и распространенных методов выбора гиперпараметров, включая K. Перекрестная проверка позволяет оценить производительность модели на разных подмножествах данных, не используя тестовую выборку для обучения.
-
Алгоритм:
- Разделите исходный набор данных на K равных частей (фолдов).
- Для каждого значения K (например, от 1 до 20 или больше):
- Для каждого фолда:
- Обучите модель KNN на всех остальных K-1 фолдах.
- Проверьте модель на текущем фолде и измерьте ее производительность (например, точность, полнота, F1-мера).
- Вычислите среднюю производительность для данного значения K по всем фолдам.
- Для каждого фолда:
- Выберите значение K, которое дало наилучшую среднюю производительность.
-
Преимущества: Дает надежную оценку производительности модели на новых данных.
-
Недостатки: Вычислительно затратен, особенно для больших наборов данных и большого диапазона значений K.
-
Пример 5-fold cross-validation:
-
-
Метод hold-out (Validation Set):
- Описание: Разделите исходный набор данных на три части: обучающую выборку, проверочную выборку (validation set) и тестовую выборку. Обучите модель KNN на обучающей выборке для разных значений K и измерьте ее производительность на проверочной выборке. Выберите значение K, которое дало наилучшую производительность на проверочной выборке. Наконец, оцените производительность выбранной модели на тестовой выборке.
- Алгоритм:
- Разделите данные на обучающий набор (обычно 70-80%), проверочный набор (10-15%) и тестовый набор (10-15%).
- Обучите KNN с разными значениями K на обучающем наборе.
- Оцените производительность каждой модели на проверочном наборе.
- Выберите K, которое дает лучшую производительность на проверочном наборе.
- Оцените финальную модель на тестовом наборе для получения оценки обобщающей способности.
- Преимущества: Проще и быстрее, чем перекрестная проверка.
- Недостатки: Менее надежна, чем перекрестная проверка, так как производительность модели зависит от конкретного разбиения данных на обучающую, проверочную и тестовую выборки.
- Как выбрать между Cross-validation и Hold-out?
- Если у вас большой объем данных, то hold-out вполне подходит.
- Если у вас мало данных, то используйте cross-validation.
- Использование кривой обучения (Learning Curve):
Алгоритм:
- Обучите KNN с разными значениями K на подмножествах обучающего набора, увеличивая размер подмножества.
- Оцените производительность каждой модели на проверочном наборе.
- Постройте график, показывающий зависимость производительности от размера обучающего набора для каждого значения K.
- Выберите K, которое дает наилучшую производительность на достаточно большом обучающем наборе и демонстрирует стабильную кривую обучения.
- Преимущества: Помогает понять, как размер обучающей выборки влияет на производительность модели и выбрать оптимальное значение K.
- Недостатки: Требует больше вычислительных ресурсов, чем hold-out.
-
Правило “квадратного корня”:
- Описание: Простое эмпирическое правило, которое рекомендует выбирать K равным квадратному корню из количества объектов в обучающей выборке: K ≈ √N, где N — количество объектов в обучающей выборке.
- Алгоритм:
- Вычислите квадратный корень из размера обучающего набора.
- Округлите результат до ближайшего целого числа.
- Используйте полученное значение в качестве K.
- Преимущества: Очень простой и быстрый способ выбора K.
- Недостатки: Не учитывает особенности данных и может не давать оптимальных результатов.
-
Правило "большого числа":
- Описание: Обычно рекомендуют брать нечетное число, чтобы избежать ничьих при голосовании (но это не всегда необходимо).
-
Визуализация принятия решений
- Для небольших размерностей (2-3 признака) можно визуализировать, как меняется граница принятия решений при разных k.
Рекомендации:
- Начните с малого диапазона значений K: Обычно, значения K от 1 до 20 достаточно для большинства задач.
- Используйте перекрестную проверку, если это возможно: Это наиболее надежный метод выбора K.
- Учитывайте размер обучающей выборки: Для больших наборов данных можно использовать большие значения K.
- Не забывайте о других гиперпараметрах: Выбор K может быть связан с выбором других гиперпараметров, таких как метрика расстояния.
- Проверяйте значения K на тестовой выборке: После того, как вы выбрали оптимальное значение K с помощью перекрестной проверки или других методов, оцените производительность модели с этим значением K на тестовой выборке, чтобы убедиться, что модель хорошо обобщает на новые данные.
Выбор оптимального значения K — это важная задача, которая требует тщательного анализа данных и экспериментов. Используйте один из описанных выше методов или их комбинацию, чтобы найти значение K, которое обеспечивает наилучшую производительность для вашей задачи.
Сравнение KNN с другими алгоритмами классификации:
Алгоритм K-ближайших соседей (KNN) является лишь одним из множества алгоритмов классификации, доступных в машинном обучении. Важно понимать сильные и слабые стороны KNN в сравнении с другими популярными алгоритмами, чтобы выбрать наиболее подходящий метод для конкретной задачи.
1. KNN vs. Логистическая регрессия (Logistic Regression):
- KNN:
- Тип алгоритма: Непараметрический, “ленивый” (lazy learner). Не строит явную модель в процессе обучения.
- Принцип работы: Классифицирует объекты на основе расстояния до ближайших соседей.
- Преимущества: Простота реализации, не требует этапа обучения.
- Недостатки: Высокая вычислительная сложность во время классификации, чувствительность к масштабу признаков, требует выбора K.
- Подходит для: Задач с нелинейными границами классов, когда важна простота и скорость прототипирования.
- Логистическая регрессия:
- Тип алгоритма: Параметрический, линейный. Строит линейную модель, описывающую вероятность принадлежности к классу.
- Принцип работы: Предсказывает вероятность принадлежности к классу на основе линейной комбинации признаков, преобразованной логистической функцией.
- Преимущества: Высокая скорость обучения и классификации, интерпретируемость (можно оценить вклад каждого признака).
- Недостатки: Предполагает линейную зависимость между признаками и целевой переменной, плохо работает с нелинейными данными.
- Подходит для: Задач с линейными границами классов, когда важна скорость и интерпретируемость модели.
2. KNN vs. Деревья решений (Decision Trees) и Случайный лес (Random Forest):
- KNN: (Описание см. выше)
- Деревья решений:
- Тип алгоритма: Непараметрический. Строит древовидную структуру, разбивающую пространство признаков на области, соответствующие разным классам.
- Принцип работы: Разбивает данные на основе последовательности вопросов, каждый из которых соответствует проверке значения одного из признаков.
- Преимущества: Интерпретируемость, способность обрабатывать категориальные и числовые признаки, устойчивость к масштабу признаков.
- Недостатки: Склонность к переобучению, нестабильность (небольшие изменения в данных могут привести к большим изменениям в структуре дерева).
- Случайный лес:
- Тип алгоритма: Ансамблевый метод, основанный на деревьях решений. Строит множество деревьев решений на случайных подмножествах данных и признаков, и объединяет их прогнозы.
- Принцип работы: Уменьшает переобучение и повышает стабильность за счет усреднения прогнозов множества деревьев.
- Преимущества: Высокая точность, устойчивость к переобучению, способность оценивать важность признаков.
- Недостатки: Меньшая интерпретируемость, чем у отдельных деревьев решений.
- Подходит для: Задач с сложными нелинейными зависимостями, когда важна высокая точность и устойчивость.
3. KNN vs. Метод опорных векторов (Support Vector Machines, SVM):
- KNN: (Описание см. выше)
- SVM:
- Тип алгоритма: Параметрический. Строит оптимальную гиперплоскость, разделяющую классы в пространстве признаков, максимизируя зазор (margin) между классами.
- Принцип работы: Находит опорные векторы (наиболее важные объекты, определяющие гиперплоскость) и строит гиперплоскость, наилучшим образом разделяющую классы.
- Преимущества: Высокая точность, эффективность в многомерном пространстве, возможность использования различных ядер (kernel functions) для обработки нелинейных данных.
- Недостатки: Сложность выбора ядра и параметров, высокая вычислительная сложность для больших наборов данных, меньшая интерпретируемость, чем у деревьев решений.
- Подходит для: Задач с высокой размерностью, когда важна высокая точность и способность обрабатывать нелинейные данные.
4. KNN vs. Наивный Байесовский классификатор (Naive Bayes):
- KNN: (Описание см. выше)
- Naive Bayes:
- Тип алгоритма: Параметрический, вероятностный. Применяет теорему Байеса с предположением о независимости признаков.
- Принцип работы: Основывается на вычислении апостериорной вероятности класса при условии заданных признаков, используя теорему Байеса и предположение о независимости признаков.
- Преимущества: Быстрая работа, простота реализации, хорошо работает с категориальными данными и небольшими объемами данных.
- Недостатки: Предположение о независимости признаков часто не выполняется на практике, что может снижать точность.
- Подходит для: Задач, где важна скорость работы и простота, особенно при работе с текстом и категориальными данными.
Таблица сравнения:
| Характеристика | KNN | Логистическая регрессия | Деревья решений | Случайный лес | SVM | Наивный Байес |
|---|---|---|---|---|---|---|
| Тип алгоритма | Непараметрический | Параметрический | Непараметрический | Ансамблевый | Параметрический | Параметрический |
| Этап обучения | Отсутствует | Присутствует | Присутствует | Присутствует | Присутствует | Присутствует |
| Сложность классификации | Высокая | Низкая | Средняя | Средняя | Высокая | Низкая |
| Интерпретируемость | Низкая | Высокая | Высокая | Средняя | Низкая | Средняя |
| Чувствительность к масштабу | Высокая | Низкая | Низкая | Низкая | Высокая (зависит от ядра) | Низкая |
| Обработка нелинейности | Хорошо | Плохо | Хорошо | Хорошо | Хорошо (с ядрами) | Плохо (предположение о независимости) |
| Переобучение | Высокая (при малом K) | Низкая | Высокая | Низкая | Зависит от параметров | Зависит от данных |
Выбор алгоритма классификации зависит от конкретной задачи, характеристик данных и требований к модели. KNN хорошо подходит для задач с нелинейными границами классов, когда важна простота и скорость прототипирования. Однако, для достижения высокой точности и устойчивости, часто более предпочтительными являются другие алгоритмы, такие как Случайный лес, SVM или логистическая регрессия (в зависимости от данных). Всегда необходимо экспериментировать с разными алгоритмами и оценивать их производительность на ваших данных, чтобы выбрать наиболее подходящий метод.
Примеры реальных задач, которые можно решить с помощью KNN в 1С:
Хотя 1С не является специализированной платформой для машинного обучения, алгоритм K-ближайших соседей (KNN) может найти применение для решения некоторых бизнес-задач непосредственно в среде 1С. Рассмотрим несколько примеров:
-
Классификация клиентов по сегментам:
- Задача: Сегментировать клиентскую базу на основе характеристик клиентов (например, история покупок, регион, тип компании) для проведения таргетированных маркетинговых кампаний.
- Признаки: Сумма покупок за период, частота покупок, средний чек, регион (кодированный числом), тип компании (кодированный числом).
- Классы: "VIP-клиенты", "Постоянные клиенты", "Новые клиенты", "Уходящие клиенты".
- Применение KNN в 1С: Реализовать KNN для автоматического отнесения новых клиентов к одному из сегментов на основе их характеристик.
-
Определение кредитоспособности заемщиков:
- Задача: Оценить риск невозврата кредита для потенциальных заемщиков.
- Признаки: Возраст, доход, кредитная история (количество просрочек, общая сумма кредитов), семейное положение, наличие имущества.
- Классы: "Кредитоспособен", "Ненадежен".
- Применение KNN в 1С: Использовать KNN для классификации заемщиков на основе их признаков и решения о выдаче кредита.
-
Прогнозирование спроса на товары:
-
Задача: Предсказать объем продаж определенного товара в следующем периоде.
-
Признаки: Объем продаж в предыдущие периоды, сезонность, цена товара, маркетинговые активности, экономические показатели.
-
Классы: (В данном случае, это задача регрессии, но KNN можно использовать для аппроксимации числового значения) Вместо классов, предсказывается само числовое значение спроса.
-
Применение KNN в 1С: Использовать KNN (для регрессии, вычисляя среднее значение у соседей) для прогнозирования спроса на основе исторических данных.
-
-
Классификация обращений в службу поддержки:
- Задача: Автоматически отнести обращения клиентов в службу поддержки к определенной категории (например, "Техническая проблема", "Вопрос по оплате", "Жалоба") для маршрутизации запросов к соответствующим специалистам.
- Признаки: Текст обращения (представленный в виде вектора слов или фраз с использованием методов обработки естественного языка, например, TF-IDF).
- Классы: "Техническая проблема", "Вопрос по оплате", "Жалоба", "Предложение".
- Применение KNN в 1С: Реализовать KNN для автоматической классификации обращений на основе их текстового содержания.
-
Выявление мошеннических операций:
- Задача: Определить подозрительные транзакции.
- Признаки: Сумма транзакции, время транзакции, географическое местоположение, IP-адрес, история транзакций пользователя.
- Классы: "Мошенническая операция", "Нормальная операция".
- Применение KNN в 1С: Использовать KNN для классификации транзакций и выявления подозрительных операций, которые отклоняются от нормального поведения.
-
Автоматическое заполнение свойств номенклатуры:
- Задача: Упростить ввод новой номенклатуры.
- Признаки: Наименование, описание (если есть)
- Классы: Значения для реквизитов (например, "Цвет", "Материал", "Размер")
- Применение KNN в 1С: На основе анализа существующих позиций номенклатуры предлагать варианты значений для свойств новой номенклатурной позиции.
-
Рекомендательные системы:
- Задача: Предлагать клиентам товары, которые они вероятно захотят приобрести.
- Признаки: Информация о прошлых покупках, просмотренные товары, демографические данные.
- Классы: Товары, которые могут быть рекомендованы.
- Применение KNN в 1С: На основе истории покупок других клиентов, предлагать текущему клиенту товары, которые приобрели "похожие" клиенты.
Важные замечания:
- Предобработка данных: Важным этапом перед применением KNN является предобработка данных, включающая очистку данных, обработку пропущенных значений, масштабирование признаков и кодирование категориальных признаков.
- Ограничения 1С: Реализация KNN в 1С может быть ограничена вычислительной мощностью платформы и отсутствием специализированных библиотек для машинного обучения. Для решения сложных задач с большими объемами данных может потребоваться использование внешних инструментов и интеграция с 1С.
- Альтернативы: В некоторых случаях, для решения тех же задач, можно использовать другие механизмы 1С, такие как правила обмена данными, бизнес-процессы и отчеты.
Алгоритм KNN может быть полезным инструментом для решения ряда бизнес-задач в 1С, особенно когда требуется простая и быстрая классификация данных. Однако, важно учитывать ограничения платформы и тщательно подходить к предобработке данных и выбору параметров алгоритма.
Рекомендации по улучшению производительности алгоритма:
Реализация алгоритма K-ближайших соседей (KNN) в 1С, как мы уже отмечали, может столкнуться с проблемами производительности, особенно при работе с большими объемами данных. Вот несколько рекомендаций по улучшению производительности:
-
Оптимизация вычисления расстояний:
- Минимизация операций: Избегайте избыточных вычислений. Например, если требуется только относительное сравнение расстояний, можно опустить вычисление квадратного корня в Евклидовом расстоянии, если он не влияет на порядок сортировки.
- Использование встроенных функций (если возможно): По возможности используйте встроенные функции 1С для математических вычислений (например, Pow() для возведения в степень).
- Кэширование вычислений: Если вычисление расстояний повторяется, рассмотрите возможность кэширования результатов, чтобы избежать повторных вычислений.
-
Эффективная структура данных:
- Выбор типа данных: Используйте наиболее эффективные типы данных для хранения данных, учитывая особенности платформы 1С. Например, если у вас много числовых данных, убедитесь, что используете правильный тип (число) с оптимальной точностью.
- Использование соответствий (Dictionaries): Используйте соответствия (Dictionaries) для быстрого поиска и доступа к данным.
- Преобразование данных: Преобразование данных в удобный для работы формат до запуска алгоритма (например, предобработка).
-
Оптимизация поиска ближайших соседей:
- Ограничение диапазона поиска: Если это возможно, ограничьте область поиска ближайших соседей. Например, если данные имеют пространственное представление (например, геолокация), можно использовать пространственные индексы для поиска ближайших точек.
- Сортировка перед выборкой: Если у вас большой массив, сортируйте только те элементы, которые нужны, а не весь массив.
-
Предварительная обработка данных:
- Масштабирование признаков (Feature Scaling): Перед вычислением расстояний масштабируйте признаки. Это особенно важно, если признаки имеют разные диапазоны значений. Используйте нормализацию (приведение значений к диапазону от 0 до 1) или стандартизацию (приведение к среднему значению 0 и стандартному отклонению 1).
- Выбор подмножества признаков (Feature Selection): Если у вас много признаков, проанализируйте их вклад в классификацию. Удалите те признаки, которые не влияют на результаты или вносят мало информации.
- Уменьшение размерности (Dimensionality Reduction): Если у вас много признаков, рассмотрите возможность уменьшения размерности данных с использованием методов, таких как метод главных компонент (PCA), чтобы сократить количество вычислений.
-
Оптимизация кода 1С:
- Избегайте циклов внутри циклов: Постарайтесь оптимизировать логику, чтобы избежать вложенных циклов, которые могут существенно замедлить выполнение кода.
- Используйте временные переменные: Используйте временные переменные для хранения промежуточных результатов, чтобы уменьшить количество обращений к данным.
- Профилирование кода: Используйте инструменты профилирования 1С для выявления узких мест в коде и оптимизации критических участков.
- Оптимизация запросов (если данные в базе): Если данные хранятся в базе данных, оптимизируйте запросы для извлечения необходимых данных. Используйте индексы, чтобы ускорить поиск.
- Разбиение на этапы: Разбейте процесс на логические этапы, чтобы было проще анализировать и оптимизировать каждый из них.
-
Использование внешних компонент (advanced):
- Внешние библиотеки: Если производительность критична, рассмотрите возможность использования внешних компонент (например, написанных на C# или C++), которые могут выполнять вычисления значительно быстрее, чем код 1С. Внешняя компонента может быть разработана для выполнения сложных математических операций, таких как вычисление расстояний или сортировка данных.
-
Кэширование результатов (Caching):
- Если обучающая выборка не меняется часто, можно кэшировать результаты вычислений (например, расстояния между объектами) для ускорения последующих классификаций.
-
Параллелизация (Parallelization) - (advanced):
- Если у вас много ядер процессора, можно рассмотреть возможность распараллеливания вычислений, например, вычисление расстояний для разных объектов обучающей выборки. Это может существенно ускорить процесс, но требует более сложной реализации. В 1С это может быть сложной задачей из-за ограничений платформы.
Выбор стратегии оптимизации:
- Простые улучшения: Начните с оптимизации вычисления расстояний и использования эффективных структур данных.
- Более сложные улучшения: Если производительность все еще недостаточна, перейдите к масштабированию признаков, выбору подмножества признаков и использованию кэширования.
- Радикальные меры: Если производительность критична, рассмотрите возможность использования внешних компонент или распараллеливания вычислений.
Важно помнить, что оптимизация производительности - это итеративный процесс. Начните с простых шагов, измерьте производительность, внесите изменения, измерьте снова и продолжайте этот цикл до тех пор, пока производительность не будет соответствовать вашим требованиям.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.17.128
Вступайте в нашу телеграмм-группу Инфостарт