Динамическая оптимизация маршрутов в 1С для поиска кратчайшего пути. Введение в Алгоритм D*-Lite

Готовая рабочая обработка для 1С 8.3 прилагается.      

В современном мире, где логистика и планирование подвержены постоянным изменениям, потребность в адаптивных алгоритмах маршрутизации становится все более актуальной. Алгоритм D*-Lite (Dynamic A* Lite) - это инкрементальный алгоритм поиска кратчайшего пути, разработанный для динамических сред, где граф маршрутов может меняться в реальном времени. В отличие от статических алгоритмов, которые требуют полного пересчета маршрута при любом изменении, D*-Lite позволяет быстро и эффективно адаптироваться к новым условиям, минимизируя вычислительные затраты.

Примеры из жизни, которые можно реализовать в 1С с помощью D-Lite:*

1. Динамическая доставка товаров: Представьте себе службу доставки, использующую 1С для управления логистикой. Маршруты доставки изначально планируются на основе текущей дорожной обстановки и доступности товаров. Однако, в течение дня могут возникать различные ситуации: пробки на дорогах, закрытие улиц из-за ремонтных работ, срочная доставка нового заказа. D*-Lite позволяет автоматически пересчитывать маршруты в реальном времени, учитывая новые условия и обеспечивая своевременную доставку.
2. Управление складской техникой: На большом складе 1С может использоваться для управления перемещением погрузчиков и других транспортных средств. Если на складе появляются временные препятствия (например, размещение новых товаров, проведение уборки), D*-Lite может помочь быстро перестроить маршруты техники, минимизируя время простоя и обеспечивая эффективное выполнение задач.
3. Оптимизация перемещения персонала: Компания имеет несколько офисов, и сотрудникам часто приходится перемещаться между ними. В 1С можно вести учет местоположения сотрудников и задач, которые им необходимо выполнить. D*-Lite может помочь оптимально спланировать маршруты сотрудников, учитывая пробки на дорогах, расписание общественного транспорта и приоритет задач. При возникновении непредвиденных обстоятельств (например, отмена встречи) маршрут может быть оперативно скорректирован.
4. Управление мобильными сотрудниками: Компания, оказывающая услуги на выезде (например, ремонт оборудования, установка программного обеспечения), использует 1С для управления мобильными бригадами. D*-Lite может помочь динамически распределять задачи между бригадами, учитывая их текущее местоположение, загруженность, пробки на дорогах и приоритет заявок. При появлении новых заявок или изменении дорожной обстановки маршруты бригад могут быть оперативно пересчитаны.

Основные принципы работы алгоритма D*-Lite

Алгоритм D*-Lite является эффективной реализацией концепции "Incremental A*", оптимизированной для динамических сред. Для понимания работы алгоритма необходимо рассмотреть несколько ключевых понятий:

1. Представление графа: Граф представляется в виде набора вершин (узлов) и ребер (связей) между ними. Каждое ребро имеет стоимость, представляющую собой, например, расстояние, время или стоимость перехода между двумя вершинами. В контексте 1С граф может быть представлен в виде массивов, таблиц значений, или других структур данных, отражающих связи между объектами и их характеристики.

2. Функция оценки стоимости (Эвристика): Как и в алгоритме A*, D*-Lite использует эвристическую функцию для оценки расстояния от текущей вершины до цели. Эвристика должна быть допустимой, то есть никогда не переоценивать фактическое расстояние до цели. Правильно подобранная эвристика позволяет алгоритму быстрее находить оптимальный путь. В 1С в качестве эвристики может использоваться, например, "евклидово расстояние" между географическими координатами, если известны координаты объектов.

3. Ключи (Keys): Каждая вершина имеет два ключа: k1 и k2. Эти ключи используются для определения приоритета вершины в очереди приоритетов. k1 отражает оценку стоимости пути от начальной вершины до цели через данную вершину, а k2 используется для разрешения конфликтов между вершинами с одинаковым k1.

4. Правая часть стоимости (rhs): Для каждой вершины вычисляется "правая часть стоимости" (rhs), представляющая собой оценку стоимости достижения цели из этой вершины, основанную на стоимости ее соседей и стоимости перехода к этим соседям.

5. Локальная согласованность (Local Consistency): Вершина считается "локально согласованной", если ее g-значение (оценка стоимости достижения вершины из начальной вершины) равно ее rhs-значению. Если вершина не локально согласованна, она помещается в очередь приоритетов для обновления.

6. Главный цикл алгоритма: Алгоритм D*-Lite работает в цикле, в котором он последовательно извлекает вершины из очереди приоритетов и обновляет их g-значения и rhs-значения. Если стоимость ребер изменяется, алгоритм обновляет rhs-значения затронутых вершин и помещает их в очередь приоритетов для пересчета.

7. Обработка изменений стоимости ребер: Ключевой особенностью D*-Lite является его способность эффективно обрабатывать изменения стоимости ребер. Когда стоимость ребра изменяется, алгоритм не пересчитывает все g-значения и rhs-значения с нуля, а только обновляет значения для тех вершин, на которые повлияло изменение. Это значительно ускоряет процесс пересчета маршрута.

8. Инкрементальность: Алгоритм D*-Lite является инкрементальным, то есть он использует результаты предыдущих вычислений для ускорения текущего поиска. При изменении графа алгоритм не пересчитывает все с нуля, а только корректирует существующее решение.

Упрощенная реализации D*-Lite в 1С:

1. Определение и инициализация графа:

&НаСервере
Процедура РассчитатьНаСервере()

    // **1. Определение графа**
    //  Представляем граф в виде массива массивов.
    //  Каждый элемент - вершина. Внутренний массив содержит связи с другими вершинами и стоимость перехода.
    Граф = Новый Массив;

    // Вершина 0
    Граф.Добавить(Новый Массив);
    Граф[0].Добавить(1);   // Связь с вершиной 1
    Граф[0].Добавить(10);  // Стоимость перехода от 0 к 1
    Граф[0].Добавить(2);   // Связь с вершиной 2
    Граф[0].Добавить(15);  // Стоимость перехода от 0 к 2

    // ... (Определение остальных вершин и связей) ...

    // Вершина 9 (Конечная)
    Граф.Добавить(Новый Массив);

    // **2. Начальная и конечная вершины**
    НачальнаяВершина = 0;
    КонечнаяВершина = 9;

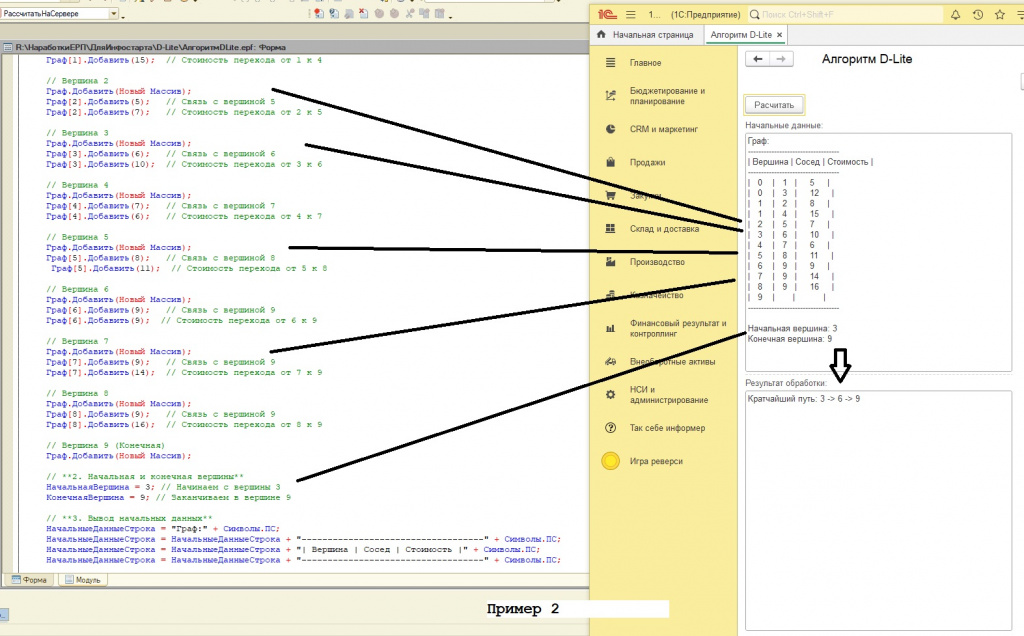
В этом блоке кода происходит определение структуры графа, который представляет собой карту маршрутов. Граф представлен в виде массива массивов. Каждый элемент внешнего массива соответствует вершине графа (например, пункту доставки, складу). Внутренний массив содержит информацию о связях этой вершины с другими вершинами, а также стоимость перехода (например, расстояние, время) между ними.

• Граф = Новый Массив; : Создается пустой массив для хранения информации о графе.
• Граф.Добавить(Новый Массив); : Добавляется новая вершина в граф.
• Граф[0].Добавить(1); Граф[0].Добавить(10); : Добавляется связь от вершины 0 к вершине 1 со стоимостью перехода 10.

Также в этом блоке определяются начальная и конечная вершины, для которых необходимо найти кратчайший путь.

2. Формирование наглядного представления графа:

    // **3. Вывод начальных данных**
    НачальныеДанныеСтрока = "Граф:" + Символы.ПС;
    НачальныеДанныеСтрока = НачальныеДанныеСтрока + "-----------------------------------" + Символы.ПС;
    НачальныеДанныеСтрока = НачальныеДанныеСтрока + "| Вершина | Сосед | Стоимость |" + Символы.ПС;
    НачальныеДанныеСтрока = НачальныеДанныеСтрока + "-----------------------------------" + Символы.ПС;

    Для i = 0 По Граф.Количество() - 1 Цикл
        Если Граф[i].Количество() = 0 Тогда
            НачальныеДанныеСтрока = НачальныеДанныеСтрока + "|   " + i + "    |       |           |" + Символы.ПС;
        Иначе
            Для j = 0 По Граф[i].Количество() - 1 Цикл
                Если j % 2 = 0 Тогда
                  НачальныеДанныеСтрока = НачальныеДанныеСтрока + "|   " + i + "    |   " + Граф[i][j] + "   |     " + Граф[i][j+1] + "     |" + Символы.ПС;
                КонецЕсли;
            КонецЦикла;
        КонецЕсли;

    КонецЦикла;
    НачальныеДанныеСтрока = НачальныеДанныеСтрока + "-----------------------------------" + Символы.ПС;
    НачальныеДанныеСтрока = НачальныеДанныеСтрока + Символы.ПС + "Начальная вершина: " + НачальнаяВершина + Символы.ПС;
    НачальныеДанныеСтрока = НачальныеДанныеСтрока + "Конечная вершина: " + КонечнаяВершина;
    ЭтотОбъект.НачальныеДанные = НачальныеДанныеСтрока;  // Заполняем реквизит формы

Этот блок кода формирует текстовое представление графа в виде таблицы для отображения в реквизите формы “НачальныеДанные”. Цель - сделать структуру графа максимально понятной для пользователя.

• НачальныеДанныеСтрока = ... : Формируется строка, содержащая заголовок таблицы, разделители и информацию о каждой вершине и ее связях.
• ЭтотОбъект.НачальныеДанные = НачальныеДанныеСтрока; : Сформированная строка присваивается реквизиту формы, чтобы пользователь мог увидеть структуру графа.

3. Реализация функции расчета расстояния:

&НаСервере
Функция Расстояние(Вершина1, Вершина2, Граф)

    Для i = 0 По Граф[Вершина1].Количество() - 1 Цикл
        Если i % 2 = 0 Тогда // Проверяем, что индекс четный (связь с вершиной)
            Если Граф[Вершина1][i] = Вершина2 Тогда
                Возврат Граф[Вершина1][i + 1]; // Возвращаем расстояние до Вершины2
            КонецЕсли;
        КонецЕсли;
    КонецЦикла;

    // Если нет прямой связи, возвращаем бесконечность (очень большое число)
    Возврат 999999;

КонецФункции

Функция Расстояние() определяет стоимость перехода между двумя заданными вершинами в графе. Она просматривает список соседей первой вершины и возвращает стоимость перехода к указанному соседу. Если прямой связи между вершинами нет, функция возвращает большое число (999999), которое интерпретируется как "бесконечность".

• Функция принимает три параметра: Вершина1 (начальная вершина), Вершина2 (конечная вершина), Граф (представление графа).
• Цикл Для i = 0 По Граф[Вершина1].Количество() - 1 Цикл: Перебирает соседей вершины Вершина1.
• Если Граф[Вершина1][i] = Вершина2 Тогда : Проверяет, является ли текущий сосед вершиной Вершина2.
• Возврат Граф[Вершина1][i + 1]; : Если сосед найден, возвращает стоимость перехода.
• Возврат 999999; : Если сосед не найден, возвращает "бесконечность".

4. Реализация упрощенного алгоритма поиска пути:

&НаСервере
Функция ВычислитьКратчайшийПуть(НачальнаяВершина, КонечнаяВершина, Граф)

    //  ВНИМАНИЕ: Это ОЧЕНЬ упрощенная версия.
    //  Реальный D*-Lite гораздо сложнее.

    //  Используем упрощенный алгоритм (что-то вроде A* без эвристики)
    ОткрытыйСписок = Новый Массив;
    ОткрытыйСписок.Добавить(НачальнаяВершина);

    Приоритеты = Новый Соответствие; // Соответствие: Вершина -> Приоритет
    Приоритеты.Вставить(НачальнаяВершина, 0);

    Предшественники = Новый Соответствие; // Соответствие: Вершина -> Предыдущая вершина на пути

    Пока ОткрытыйСписок.Количество() > 0 Цикл

        // Находим вершину с наименьшим приоритетом в ОткрытомСписке
        ТекущаяВершина = Неопределено;
        МинПриоритет = 999999;

        Для Каждого Вершина Из ОткрытыйСписок Цикл
            Если Приоритеты.Получить(Вершина) < МинПриоритет Тогда
                МинПриоритет = Приоритеты.Получить(Вершина);
                ТекущаяВершина = Вершина;
            КонецЕсли;
        КонецЦикла;

        Если ТекущаяВершина = Неопределено Тогда
            Прервать; // Нет доступных вершин
        КонецЕсли;

        // Если достигли конечной вершины, восстанавливаем путь
        Если ТекущаяВершина = КонечнаяВершина Тогда
            Путь = "";
            Вершина = КонечнаяВершина;

            Пока Вершина <> Неопределено Цикл
                Путь = Строка(Вершина) + " -> " + Путь; // Явное преобразование числа в строку
                Вершина = Предшественники.Получить(Вершина);
            КонецЦикла;

            Возврат Лев(Путь, СтрДлина(Путь) - 4); // Удаляем " -> " в конце
        КонецЕсли;

        // Удаляем текущую вершину из ОткрытогоСписке
        ИндексУдаляемойВершины = ОткрытыйСписок.Найти(ТекущаяВершина);

        Если ИндексУдаляемойВершины <> Неопределено Тогда
           ОткрытыйСписок.Удалить(ИндексУдаляемойВершины);
        КонецЕсли;

        // Просматриваем соседей текущей вершины
        Для i = 0 По Граф[ТекущаяВершина].Количество() - 1 Цикл
            Если i % 2 = 0 Тогда // Проверяем, что индекс четный (связь с вершиной)
                Сосед = Граф[ТекущаяВершина][i];
                РасстояниеДоСоседа = Расстояние(ТекущаяВершина, Сосед, Граф);

                Если Приоритеты.Получить(Сосед) = Неопределено Тогда
                    ПриоритетСоседа = 999999; // Бесконечность
                Иначе
                    ПриоритетСоседа = Приоритеты.Получить(Сосед);
                КонецЕсли;

                НовыйПриоритет = МинПриоритет + РасстояниеДоСоседа;

                Если НовыйПриоритет < ПриоритетСоседа Тогда
                    Приоритеты.Вставить(Сосед, НовыйПриоритет);
                    Предшественники.Вставить(Сосед, ТекущаяВершина);

                    Если ОткрытыйСписок.Найти(Сосед) = Неопределено Тогда
                        ОткрытыйСписок.Добавить(Сосед);
                    КонецЕсли;
                КонецЕсли;
            КонецЕсли;
        КонецЦикла;
    КонецЦикла;

    Возврат "Путь не найден";

КонецФункции

Функция ВычислитьКратчайшийПуть() реализует упрощенную версию алгоритма поиска кратчайшего пути, напоминающую A*, но без эвристики и с упрощенной логикой обновления. Она использует следующие структуры данных:

• ОткрытыйСписок : Массив вершин, которые необходимо посетить.
• Приоритеты : Соответствие, которое хранит приоритет каждой вершины (оценку стоимости достижения цели через эту вершину).
• Предшественники : Соответствие, которое хранит информацию о предыдущей вершине на пути к каждой вершине.

Алгоритм итеративно выбирает вершину с наименьшим приоритетом из открытого списка, просматривает ее соседей и обновляет их приоритеты и предшественников. Цикл продолжается до тех пор, пока не будет достигнута конечная вершина или открытый список не станет пустым.

5. Завершение процедуры РассчитатьНаСервере():

    // **3. Вычисление кратчайшего пути**
    Путь = ВычислитьКратчайшийПуть(НачальнаяВершина, КонечнаяВершина, Граф);

    // **4. Вывод результата**
    РезультатОбработкиСтрока = "Кратчайший путь: " + Путь;
    ЭтотОбъект.РезультатОбработки = РезультатОбработкиСтрока; // Заполняем реквизит формы

КонецПроцедуры

В заключительной части процедуры РассчитатьНаСервере() вызывается функция ВычислитьКратчайшийПуть() для нахождения кратчайшего пути. Результат, полученный от функции, присваивается реквизиту формы "РезультатОбработки", чтобы пользователь мог увидеть найденный маршрут.

Представленный код реализует упрощенный алгоритм поиска пути на графе. Основная цель - продемонстрировать базовые принципы работы алгоритмов поиска пути в контексте 1С. Однако, он не обладает ключевыми особенностями алгоритма D*-Lite, такими как инкрементальное обновление и адаптация к динамическим изменениям в графе. В следующих шагах мы обсудим, как можно развить этот пример в сторону более полноценной реализации D*-Lite.

Дальнейшее развитие и оптимизация

Представленный пример является лишь отправной точкой для реализации алгоритма D*-Lite в 1С. Для создания полноценного решения, пригодного для практического применения, необходимо реализовать ряд улучшений и оптимизаций.

1. Реализация инкрементального обновления:

Ключевой особенностью D*-Lite является возможность быстрого пересчета маршрутов при изменении графа. Для этого необходимо реализовать следующие шаги:

• Отслеживание изменений в графе: Необходимо реализовать механизм, позволяющий отслеживать изменения в стоимости ребер (например, изменение времени доставки, появление новых препятствий). В 1С это можно сделать, используя подписки на события.
• Обновление rhs-значений: При изменении стоимости ребра необходимо обновить rhs-значения вершин, которые зависят от этого ребра.
• Помещение вершин в очередь приоритетов: Вершины, rhs-значения которых были изменены, необходимо поместить в очередь приоритетов для пересчета g-значений.
• Пересчет g-значений: В цикле алгоритма необходимо пересчитывать g-значения вершин, извлеченных из очереди приоритетов, и распространять изменения на их соседей.

2. Использование более эффективных структур данных:

Массивы, использованные в примере, могут быть неэффективны для работы с большими графами. Рекомендуется рассмотреть возможность использования других структур данных, таких как:

• Таблица значений: Позволяет хранить данные в табличном виде и использовать индексы для быстрого поиска.
• Коллекции (Соответствие, Список): Предоставляют более гибкие возможности для хранения и манипулирования данными, чем массивы.

При выборе структуры данных необходимо учитывать особенности задачи и требования к производительности.

3. Оптимизация алгоритма поиска:

• Эвристическая функция: Добавление эвристической функции позволяет значительно ускорить поиск кратчайшего пути. Эвристическая функция должна оценивать расстояние от текущей вершины до цели и быть допустимой (никогда не переоценивать фактическое расстояние).
• Эффективная очередь приоритетов: Использование эффективной реализации очереди приоритетов (например, на основе бинарной кучи) позволяет быстро извлекать вершину с наименьшим приоритетом.

4. Масштабирование:

При работе с большими графами необходимо учитывать ограничения 1С и принимать меры для повышения производительности:

• Разделение графа: Можно разбить большой граф на несколько меньших графов и обрабатывать их параллельно.
• Использование внешних компонент: Для выполнения ресурсоемких операций можно использовать внешние компоненты, разработанные на других языках программирования (например, C++).

5. Визуализация:

Для упрощения отладки и мониторинга работы алгоритма рекомендуется реализовать визуализацию графа и процесса поиска пути. В 1С это можно сделать с помощью графической схемы или внешних инструментов визуализации.

В заключение:

В данной статье мы рассмотрели возможность применения алгоритма D*-Lite для решения задач динамической маршрутизации в 1С. Несмотря на то, что 1С не является платформой, изначально ориентированной на сложные вычислительные алгоритмы, продемонстрирована принципиальная возможность реализации базовых элементов D*-Lite. Представленный упрощенный пример показывает, как можно представить граф, реализовать функцию расчета расстояния и использовать алгоритм поиска пути для нахождения оптимального маршрута.

Ключевое преимущество D-Lite перед другими алгоритмами поиска маршрута, такими как A или алгоритм Дейкстры, заключается в его способности эффективно работать в динамически меняющихся средах. В то время как A* и Дейкстра требуют полного пересчета маршрута при каждом изменении графа (например, при появлении новых препятствий или изменении стоимости дорог), D*-Lite пересчитывает только часть графа, затронутую изменениями. Это делает его значительно более эффективным в ситуациях, когда маршрут необходимо оперативно корректировать в реальном времени. Например, при изменении дорожной обстановки (пробки, аварии) или при появлении новых заказов на доставку, D*-Lite позволяет быстро адаптировать маршруты, минимизируя задержки и повышая эффективность логистики.**

Реализация полноценного D*-Lite в 1С потребует значительных усилий по оптимизации кода, выбору эффективных структур данных и разработке механизмов обработки динамических изменений в графе. Однако, в ряде бизнес-сценариев, где важна адаптация к изменяющимся условиям, применение D*-Lite может принести значительную пользу, повышая эффективность логистики, управления транспортом и перемещения персонала.

Дальнейшие направления развития данной темы включают:

• Изучение и реализация продвинутых техник оптимизации кода 1С.
• Исследование возможности использования внешних компонент или интеграции с внешними сервисами для реализации вычислительно-интенсивных частей алгоритма.
• Разработка специализированных пользовательских интерфейсов для визуализации графа маршрутов и управления параметрами алгоритма.

Несмотря на сложности, связанные с реализацией D*-Lite в 1С, перспективы его применения для решения задач динамической маршрутизации остаются весьма интересными и заслуживают дальнейшего изучения.

P.S. 

• Другие алгоритмы поиска оптимального маршрута в моем профиле (с примерами и рабочими обработками)
• См. скриншоты к статье: в них результаты работы обработки и места ввода начальных данных для тестирования с вашими данными.