Треугольник Паскаля, эта геометрическая фигура, столь простая в своем построении и одновременно поражающая глубиной заложенных в ней математических закономерностей, на протяжении веков привлекает внимание ученых, математиков и просто любителей прекрасного. Его история уходит корнями в древние цивилизации, а свойства находят применение в самых разнообразных областях науки и техники, от теории вероятностей до информатики. Изучение треугольника Паскаля – это не просто знакомство с математическим объектом, это погружение в мир удивительных связей и гармонии, царящих в мире чисел.
Первые упоминания о структурах, аналогичных треугольнику Паскаля, встречаются в трудах древних индийских математиков, живших задолго до рождения Блеза Паскаля. Так, еще в X веке индийский математик Хайяма изучал числовые закономерности, которые можно представить в виде треугольной таблицы. Однако систематическое изучение свойств и широкое распространение эта структура получила благодаря работам именно Блеза Паскаля, французского математика, физика, философа и писателя XVII века. В своем “Трактате об арифметическом треугольнике”, опубликованном в 1654 году, Паскаль подробно описал свойства этой фигуры и продемонстрировал ее применение в решении различных задач, в частности, в теории вероятностей. Именно поэтому за этой структурой прочно закрепилось название "треугольник Паскаля", хотя справедливо было бы отметить вклад и других ученых в его изучение.
Построение треугольника Паскаля осуществляется по очень простому правилу. На вершине треугольника располагается единица. Каждая последующая строка начинается и заканчивается единицей, а остальные элементы строки вычисляются как сумма двух элементов, расположенных непосредственно над ними в предыдущей строке. Таким образом, каждый элемент треугольника представляет собой биномиальный коэффициент, который обозначается как C(n, k), где n – номер строки (начиная с 0), а k – номер элемента в строке (тоже начиная с 0). Биномиальный коэффициент C(n, k) показывает количество способов выбора k элементов из множества, состоящего из n элементов. Это число также называют сочетанием из n по k.
Математически биномиальный коэффициент C(n, k) можно выразить следующей формулой:
C(n, k) = n! / (k! * (n - k)!)
где n! (читается "n факториал") – это произведение всех натуральных чисел от 1 до n. Например, 5! = 1 * 2 * 3 * 4 * 5 = 120. Эта формула позволяет вычислить любой элемент треугольника Паскаля, не прибегая к его построению.
Треугольник Паскаля обладает множеством удивительных свойств. Сумма элементов в каждой строке равна 2 в степени n, где n – номер строки. Например, в строке с номером 3 (1 3 3 1) сумма элементов равна 1 + 3 + 3 + 1 = 8 = 2^3. Элементы, расположенные симметрично относительно середины строки, равны друг другу. Это свойство является следствием того, что C(n, k) = C(n, n - k). Если из каждого элемента треугольника Паскаля вычесть единицу, то полученные числа будут соответствовать коэффициентам разложения многочлена (x + 1)^n. Диагонали треугольника Паскаля также содержат интересные числовые последовательности. Первая диагональ состоит из единиц, вторая – из натуральных чисел, третья – из треугольных чисел (1, 3, 6, 10, 15 и т.д.), четвертая – из тетраэдральных чисел (1, 4, 10, 20, 35 и т.д.) и так далее.
Треугольник Паскаля тесно связан с теорией вероятностей. Как уже упоминалось, его элементы представляют собой биномиальные коэффициенты, которые используются для вычисления вероятностей в схеме Бернулли. Схема Бернулли описывает последовательность независимых испытаний, в каждом из которых может произойти либо успех, либо неудача. Вероятность успеха во всех испытаниях одинакова. Биномиальный коэффициент C(n, k) позволяет вычислить вероятность того, что в n испытаниях произойдет ровно k успехов. Например, если мы подбрасываем монету 5 раз, то вероятность выпадения ровно 2 орлов можно вычислить как C(5, 2) * (1/2)^2 * (1/2)^3 = 10 * (1/4) * (1/8) = 5/16.
В информатике треугольник Паскаля находит применение в различных алгоритмах и структурах данных. Например, его можно использовать для быстрого вычисления биномиальных коэффициентов, необходимых во многих комбинаторных задачах. Кроме того, треугольник Паскаля можно использовать для реализации алгоритмов сжатия данных, а также для построения фрактальных изображений, таких как треугольник Серпинского.
Одним из конкурентов треугольника Паскаля в плане вычисления биномиальных коэффициентов являются рекурсивные алгоритмы. Рекурсивный алгоритм вычисления C(n, k) основан на следующем соотношении:
C(n, k) = C(n - 1, k - 1) + C(n - 1, k)
Этот алгоритм очень прост в реализации, однако он обладает существенным недостатком – высокой вычислительной сложностью. Дело в том, что при каждом рекурсивном вызове происходит многократное пересчитывание одних и тех же значений, что приводит к экспоненциальному росту времени выполнения. В отличие от рекурсивного алгоритма, построение треугольника Паскаля позволяет вычислить все биномиальные коэффициенты до заданного значения n за время O(n^2), что значительно быстрее. Еще одним конкурентом является непосредственное вычисление по формуле с факториалами. Однако вычисление факториалов для больших чисел может приводить к переполнению и требует использования специальных библиотек для работы с длинной арифметикой. В этом плане, треугольник Паскаля также является более предпочтительным, так как значения его элементов растут не так быстро, как факториалы.
Треугольник Паскаля остается актуальным и в наши дни. Он продолжает использоваться в различных областях науки и техники, а также является прекрасным инструментом для обучения математике. Его простота и наглядность позволяют легко понять основные принципы комбинаторики и теории вероятностей, а также развивают логическое мышление и умение видеть закономерности. Изучение треугольника Паскаля – это не только полезно, но и увлекательно, ведь он открывает перед нами удивительный мир математики, полный загадок и красоты.
Прежде всего, стоит обратить внимание на удивительную связь треугольника Паскаля с числами Фибоначчи. Если аккуратно просуммировать элементы треугольника Паскаля, расположенные вдоль диагоналей, идущих слева направо снизу вверх, то мы получим последовательность чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13 и так далее. Эта последовательность, где каждое последующее число является суммой двух предыдущих, встречается в самых неожиданных местах, от биологии (расположение листьев на стебле) до искусства (пропорции золотого сечения). Само существование столь тесной связи между треугольником Паскаля и числами Фибоначчи свидетельствует о глубокой внутренней гармонии математики.
Связь между треугольником Паскаля и числами Каталана проявляется в том, что числа Каталана могут быть выражены через биномиальные коэффициенты, которые, как известно, составляют элементы треугольника Паскаля. Это еще раз подчеркивает универсальность и взаимосвязанность математических объектов.
Однако, не стоит ограничиваться только комбинаторными объектами. Треугольник Паскаля также имеет неожиданные связи с аналитической теорией чисел, в частности, с дзета-функцией Римана. Дзета-функция Римана, определяемая как бесконечная сумма обратных степеней натуральных чисел, является одним из самых загадочных объектов в математике. Ее нули, согласно гипотезе Римана, определяют распределение простых чисел, а значит, и структуру всей арифметики. Связь между треугольником Паскаля и дзета-функцией Римана проявляется в том, что некоторые значения дзета-функции могут быть выражены через биномиальные коэффициенты, составляющие элементы треугольника Паскаля. Эта связь пока не до конца изучена, но она открывает захватывающие перспективы для дальнейших исследований.
Помимо изучения связей треугольника Паскаля с другими математическими объектами, интересно рассмотреть его обобщения на случай многочленов с большим числом переменных. Классический треугольник Паскаля соответствует разложению бинома (a + b)^n, где n - натуральное число. Однако, можно рассмотреть разложение тринома (a + b + c)^n, тетранома (a + b + c + d)^n и так далее. В этих случаях вместо треугольника получается многомерная пирамида, элементы которой также являются обобщенными биномиальными коэффициентами. Изучение свойств этих многомерных пирамид представляет собой интересную задачу комбинаторной геометрии.
Еще одним направлением исследований является обобщение треугольника Паскаля на случай бесконечных треугольников. В классическом треугольнике Паскаля каждая строка имеет конечное число элементов. Однако, можно рассмотреть бесконечные треугольники, где каждая строка имеет бесконечное число элементов. Элементы таких треугольников могут быть определены с помощью различных рекуррентных соотношений, аналогичных тому, которое используется для построения классического треугольника Паскаля. Изучение свойств этих бесконечных треугольников представляет собой интересную задачу теории разностных уравнений.
Наконец, стоит отметить, что треугольник Паскаля имеет многочисленные приложения в различных областях науки и техники. В комбинаторике он используется для вычисления вероятностей в задачах теории вероятностей и статистики. В информатике он используется для построения эффективных алгоритмов сортировки и поиска. В физике он которое может привести к новым открытиям и приложениям в различных областях науки и техники. Связь треугольника Паскаля с числами Фибоначчи, числами Каталана и дзета-функцией Римана подчеркивает его фундаментальную роль в математике. Обобщения треугольника Паскаля на случай многочленов с большим числом переменных и на случай бесконечных треугольников открывают новые возможности для исследований в комбинаторике, геометрии и теории разностных уравнений. Наконец, многочисленные приложения треугольника Паскаля в различных областях науки и техники свидетельствуют о его практической значимости.
Продолжая углубляться в математические дебри, окружающие треугольник Паскаля, нельзя не затронуть тему его связи с теорией вероятностей. Именно благодаря работам Паскаля, изучавшего азартные игры, и возник этот замечательный треугольник. Каждый элемент треугольника, как мы уже знаем, представляет собой биномиальный коэффициент, который, в свою очередь, позволяет вычислять вероятности различных событий в схеме Бернулли. Представьте себе, что мы многократно подбрасываем монету. Какова вероятность того, что из n бросков ровно k раз выпадет орёл? Ответ на этот вопрос даёт соответствующий биномиальный коэффициент, расположенный в треугольнике Паскаля. Эта связь делает треугольник Паскаля незаменимым инструментом в статистическом анализе и моделировании случайных процессов.
Более того, треугольник Паскаля тесно связан с понятием нормального распределения, одного из самых важных распределений в статистике. Если мы построим гистограмму, отображающую распределение биномиальных коэффициентов в строке треугольника Паскаля, то при увеличении номера строки эта гистограмма будет всё больше и больше напоминать колоколообразную кривую нормального распределения. Этот факт, известный как теорема Муавра-Лапласа, демонстрирует глубокую связь между дискретными и непрерывными математическими объектами.
Помимо вероятности и статистики, треугольник Паскаля находит применение в теории кодирования, науке, занимающейся разработкой методов надежной передачи информации по зашумлённым каналам связи. В частности, коды Рида-Маллера, используемые в различных приложениях, от космической связи до хранения данных на компакт-дисках, тесно связаны с биномиальными коэффициентами и, следовательно, с треугольником Паскаля. Эти коды обладают способностью исправлять ошибки, возникающие при передаче информации, и их эффективность во многом определяется математическими свойствами треугольника Паскаля.
Интересным направлением исследований является изучение q-аналогов треугольника Паскаля. Q-аналоги — это обобщения математических объектов, зависящие от параметра q, и переходящие в исходные объекты при q, стремящемся к 1. Q-аналоги треугольника Паскаля возникают в различных областях математики, от комбинаторики до теории представлений, и их изучение позволяет получить новые insights в структуру классического треугольника Паскаля.
Также стоит упомянуть о связи треугольника Паскаля с фракталами, математическими объектами, обладающими свойством самоподобия. Если в треугольнике Паскаля закрасить все элементы, делящиеся на 2, то получится фрактал, известный как треугольник Серпинского. Этот треугольник, обладающий бесконечной детализацией, демонстрирует ещё одну неожиданную связь треугольника Паскаля с другими областями математики.
Более глубокое изучение может быть направлено на изучение его применения в численном анализе, в частности, при построении интерполяционных многочленов. Формула Ньютона для интерполяции, использующая конечные разности, тесно связана с биномиальными коэффициентами и, следовательно, с треугольником Паскаля. Эта связь позволяет строить эффективные алгоритмы для приближенного вычисления значений функций.
В заключение, треугольник Паскаля — это удивительный математический объект, который продолжает вдохновлять исследователей на новые открытия и обобщения.
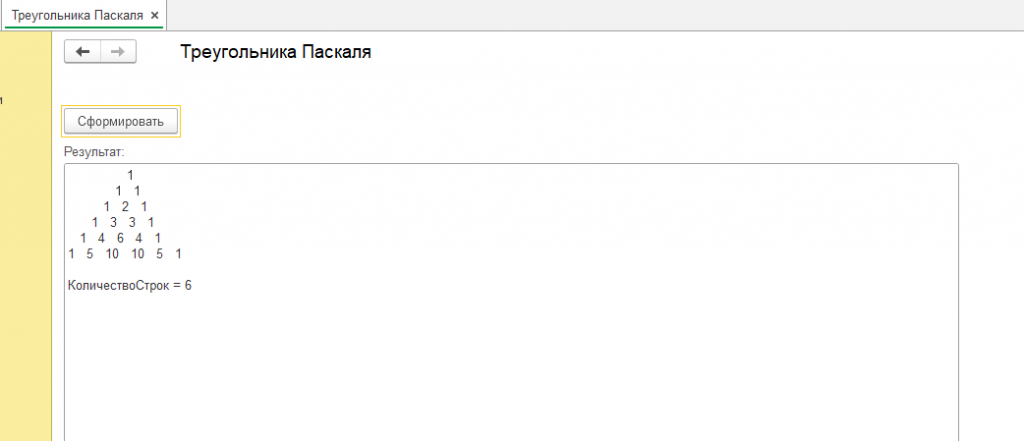
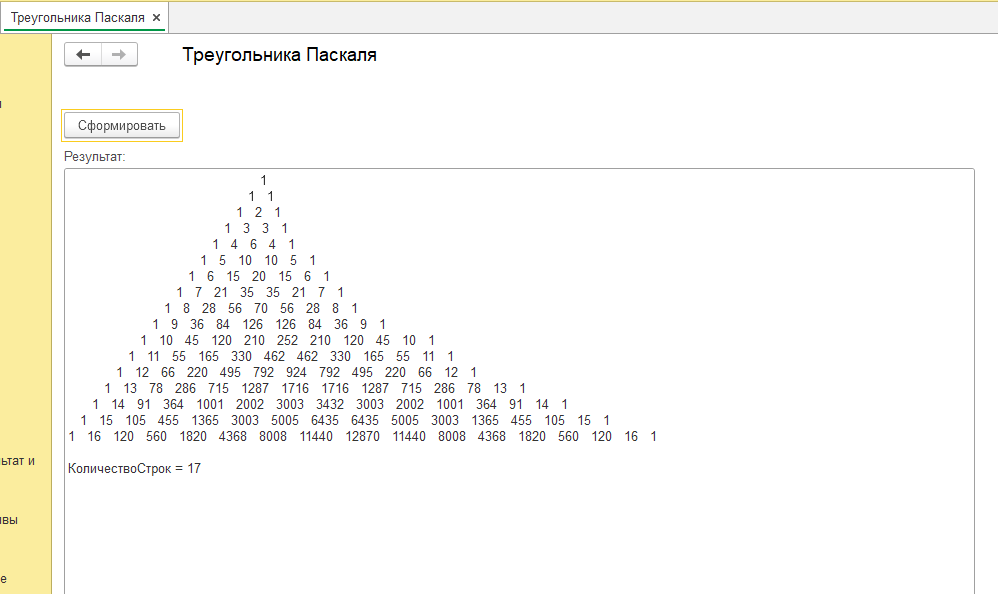
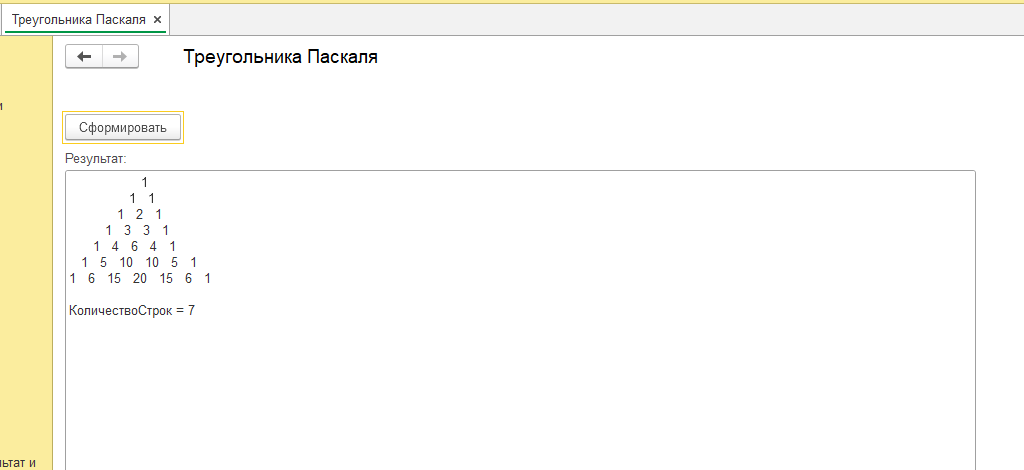
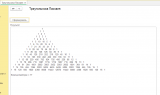
Для наглядности прилагаю обработку для 1с 8.3, которая будет работать во всех 1С 8.3 на управляемых формах, будет интересна как обычному пользователю, так и начинающему программисту. Обработка строит Треугольник Паскаля.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.13.82
Вступайте в нашу телеграмм-группу Инфостарт