Статья для начинающих программистов, реализуем три варианта выполнения Бинома Ньютона в 1С 8.3.
Бином Ньютона – это фундаментальная теорема в алгебре, описывающая разложение бинома (суммы двух слагаемых, возведенной в целую неотрицательную степень) в сумму одночленов. Его элегантность и практическая значимость сделали его неотъемлемой частью математического аппарата, применяемого во многих областях науки и техники. Формула, открытая еще в XVII веке, носящая имя великого английского математика Исаака Ньютона, позволяет избежать громоздких вычислений при возведении бинома в высокую степень, предоставляя эффективный метод вычисления каждого члена разложения. Разложение бинома по формуле Ньютона является результатом многовековых усилий математиков, начавшихся еще с работ древнегреческих ученых, занимавшихся изучением арифметических и геометрических прогрессий, которые лежат в основе комбинаторных свойств биномиальных коэффициентов. Исследование биномиальных коэффициентов и их связей с комбинаторными задачами – это отдельная, обширная область математики, тесно переплетающаяся с теорией вероятностей и другими разделами дискретной математики.
Разложение бинома по формуле Ньютона не ограничивается только целыми неотрицательными степенями. С помощью методов математического анализа, в частности, использования рядов Тейлора, формула может быть обобщена на произвольные вещественные, а в некоторых случаях и комплексные показатели степени. Это открывает возможности для применения бинома Ньютона в задачах, выходящих далеко за рамки элементарной алгебры. Например, в математическом анализе бином Ньютона играет важную роль при вычислении производных и интегралов, а также в теории дифференциальных уравнений. Его использование в этих областях позволяет упростить сложные вычисления и получить компактные аналитические выражения для решения задач. Зачастую, знание биномиального разложения позволяет эффективно приближать сложные функции с помощью полиномов, что является основой для многих численных методов.
В теории вероятностей биномиальное распределение, основанное на биномиальной теореме, используется для моделирования вероятности наступления события в серии независимых испытаний. Биномиальный коэффициент в этом контексте интерпретируется как число способов выбора k успешных исходов из n испытаний. Понимание биномиального распределения и его свойств является ключом к решению многих задач в статистике, особенно при анализе данных, полученных в результате экспериментов с дискретными случайными величинами. Биномиальное распределение является фундаментальной моделью для описания случайных явлений во многих областях, от медицины и биологии до экономики и финансов. Его применимость обусловлена его простотой и наглядностью, позволяющей легко интерпретировать результаты.
Биномиальная теорема тесно связана с понятием комбинаторных чисел, или чисел сочетаний. Биномиальный коэффициент "n по k" (обозначается как C(n, k) или nCk) показывает количество способов выбора k элементов из множества, содержащего n элементов. Эти числа обладают множеством замечательных свойств, которые активно используются в комбинаторике и теории вероятностей. Например, биномиальный коэффициент симметричен, то есть C(n, k) = C(n, n-k), что отражает интуитивно понятное свойство: количество способов выбрать k элементов равно количеству способов выбрать оставшиеся n-k элементов. Это свойство часто используется для упрощения вычислений. Паскальев треугольник, наглядно представляющий биномиальные коэффициенты, является одним из самых известных и красивых геометрических представлений биномиальной теоремы. Его структура демонстрирует рекуррентные соотношения между биномиальными коэффициентами.
Паскалев треугольник, названный в честь французского математика Блеза Паскаля, хотя и известный задолго до него, представляет собой бесконечный треугольник, элементами которого являются биномиальные коэффициенты. Каждый элемент треугольника является суммой двух соседних элементов в предыдущей строке, что отражает рекуррентное соотношение C(n, k) = C(n-1, k-1) + C(n-1, k). Эта рекурсия позволяет эффективно вычислять биномиальные коэффициенты для больших значений n и k, избегая необходимости использования формулы факториалов. Паскалев треугольник обладает множеством замечательных свойств и симметрий, что делает его объектом изучения не только в математике, но и в искусстве и архитектуре. Его элементы часто появляются в различных комбинаторных задачах, что делает его универсальным инструментом для решения таких задач. Изучение Паскалева треугольника позволяет наглядно понять свойства биномиальных коэффициентов и их взаимосвязь.
В основе биномиальной теоремы лежат комбинаторные принципы, позволяющие подсчитывать количество различных комбинаций элементов. При возведении бинома (a+b)^n в степень n, каждый член разложения представляет собой произведение степеней a и b, умноженное на соответствующий биномиальный коэффициент. Этот коэффициент показывает количество способов выбрать определенное число элементов a из n элементов, причем порядок выбора не имеет значения. Именно поэтому биномиальные коэффициенты являются ключевыми элементами формулы Ньютона. Они представляют собой количество способов, которыми можно выбрать k успехов из n независимых испытаний Бернулли, что делает их фундаментальными для теории вероятностей. Использование комбинаторных принципов позволяет получить не только формулу Ньютона, но и понять её интуитивное значение и применимость.
В отличие от приближенных методов, бином Ньютона дает точное разложение бинома. Это делает его незаменимым инструментом в задачах, где требуется точность вычислений. Однако, для высоких степеней n вычисления могут стать громоздкими, хотя и значительно менее громоздкими, чем прямой расчет. В таких случаях могут применяться приближенные методы, такие как асимптотические разложения или использование приближенных формул для биномиальных коэффициентов. Эти приближенные методы, хотя и не обеспечивают абсолютной точности, позволяют получить достаточно точный результат за меньшее время. Выбор между точным и приближенным методом зависит от требуемой точности и вычислительных ресурсов.
Биномиальная теорема нашла широкое применение в различных областях науки и техники. Она используется в физике для вычисления вероятности распределения частиц, в химии для описания вероятностей химических реакций, в экономике для моделирования финансовых процессов, в информатике для анализа алгоритмов и структур данных. В каждой из этих областей бином Ньютона позволяет упростить вычисления и получить компактные аналитические выражения. Его универсальность и эффективность сделали его одним из самых важных инструментов математического анализа. Возможности его применения постоянно расширяются с развитием новых областей науки и техники.
Одним из важных обобщений бинома Ньютона является многочленное разложение, которое позволяет разложить в ряд сумму более чем двух слагаемых, возведенных в целую неотрицательную степень. Это разложение, хотя и более сложное, также основано на комбинаторных принципах и использует многомерные биномиальные коэффициенты. Многочленное разложение играет важную роль в многомерном математическом анализе и теории вероятностей, позволяя эффективно работать с многомерными случайными величинами. Использование многочленного разложения позволяет упростить вычисления и получить компактные аналитические выражения для решения многомерных задач.
В контексте многочленного разложения, биномиальный коэффициент обобщается на многомерный биномиальный коэффициент. Этот коэффициент показывает количество способов разложить целое число n на сумму k целых неотрицательных слагаемых. Многомерные биномиальные коэффициенты имеют широкое применение в задачах теории вероятностей, статистики и комбинаторики, особенно при работе с многомерными распределениями. Их свойства и взаимосвязи изучаются в рамках многомерного комбинаторного анализа. Понимание многомерных биномиальных коэффициентов важно для решения сложных комбинаторных задач.
Аппроксимация функций с помощью биномиального разложения - важная область применения данного метода. В тех случаях, где точное вычисление значения функции затруднительно, бином Ньютона позволяет получить достаточно точное приближение функции с помощью полиномиальных функций. Точность аппроксимации зависит от степени полинома и свойств приближаемой функции. Метод находит широкое применение в численном анализе, особенно в задачах решения дифференциальных уравнений и интегральных уравнений. Этот подход позволяет заменять сложные вычисления на более простые и быстрые.
Связь бинома Ньютона с другими математическими объектами, такими как числа Фибоначчи, является ещё одним интересным аспектом его изучения. Числа Фибоначчи, определяемые рекуррентным соотношением, также проявляются в различных комбинаторных задачах и имеют неожиданные связи с биномиальными коэффициентами. Исследование этих связей помогает глубже понять как структуру биномиального разложения, так и свойства чисел Фибоначчи. Это приводит к новым открытиям и обобщениям в обоих направлениях.
Биномиальное разложение применяется в вычислительной математике для построения различных численных методов. Например, метод Ньютона-Рафсона для нахождения корней уравнений основан на биномиальном приближении функции в окрестности точки. Это позволяет эффективно приближаться к корню уравнения итеративным путем. Использование биномиального разложения в численных методах позволяет повысить их эффективность и точность. Различные модификации и обобщения биномиального разложения используются в разных областях вычислительной математики.
Применимость бинома Ньютона в задачах анализа данных и машинного обучения обусловлена его способностью приближать сложные функции с помощью полиномов. Полиномиальные аппроксимации используются в различных алгоритмах машинного обучения для построения моделей и прогнозирования. Бином Ньютона, будучи фундаментальной основой для таких аппроксимаций, способствует развитию и улучшению этих алгоритмов. Этот аспект его применения активно развивается с ростом возможностей вычислительной техники и появлением новых алгоритмов машинного обучения.
В финансовой математике бином Ньютона используется для моделирования и оценки опционов. Биномиальная модель опционов - один из наиболее простых и наглядных методов оценки опционов, основанных на дискретном времени. Эта модель позволяет определить справедливую цену опциона, учитывая вероятность изменения цены базового актива в будущем. Биномиальная модель опционов используется как для обучения, так и для практического применения в финансовых учреждениях.
Актуальность применения бинома Ньютона в программировании связана с необходимостью обработки больших объемов данных и эффективного решения сложных вычислительных задач. В частности, биномиальные коэффициенты широко применяются в алгоритмах, связанных с комбинаторикой и теорией вероятностей. Понимание биномиальной теоремы помогает разработчикам создавать более эффективные и оптимизированные алгоритмы. Оптимизация вычислений биномиальных коэффициентов является важной задачей в программировании, позволяющая ускорить работу приложений.
Ограничения применения бинома Ньютона связаны с его сложностью для высоких степеней и необходимостью точного вычисления факториалов. Для больших значений n и k, вычисление биномиальных коэффициентов может занимать значительное время и вычислительные ресурсы. В таких случаях, как уже упоминалось, применяются приближенные методы, которые позволяют получить достаточно точный результат за меньшее время. Выбор метода зависит от конкретной задачи и требований к точности.
Подводя итог, можно сказать, что бином Ньютона — это мощный математический инструмент, его значение выходит далеко за рамки элементарной алгебры. Его применение в самых разных областях науки и техники постоянно расширяется, отражая его фундаментальную роль в математическом аппарате. Несмотря на определенные ограничения в вычислениях для высоких степеней, его точность и элегантность делают его незаменимым для решения широкого круга задач. Понимание биномиальной теоремы и её обобщений является неотъемлемой частью математической подготовки во многих областях, и его изучение способствует развитию математического мышления и способности к решению сложных проблем.
P.S.
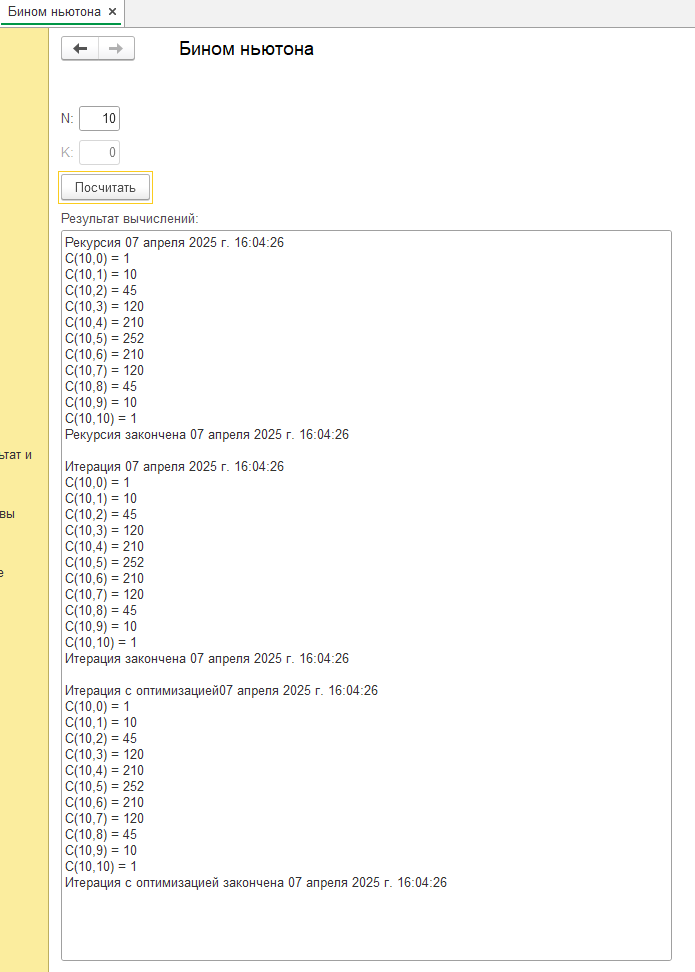
- Обработку приложил к статье. Выполняет три метода реализации Бинома Ньютона (см. скриншоты). Нужно выставить n в обработке и нажать "посчитать"
- Про треугольник Паскаля писал в предыдущей статье
Метод рекурсивный:
Функция БиномНьютонаРекурсия(n, k)
Если k = 0 Тогда
Возврат 1;
ИначеЕсли k = n Тогда
Возврат 1;
ИначеЕсли k > n Тогда
Возврат 0;
Иначе
Возврат БиномНьютонаРекурсия(n - 1, k - 1) + БиномНьютонаРекурсия(n - 1, k);
КонецЕсли;
КонецФункции
Итеративный метод:
//////////////////
Функция Факториал(n)
Результат = 1;
Если n > 1 Тогда
Для i = 2 По n Цикл
Результат = Результат * i;
КонецЦикла;
КонецЕсли;
Возврат Результат;
КонецФункции
Функция БиномНьютонаИтерация(n, k)
Если k < 0 Или k > n Тогда
Возврат 0;
ИначеЕсли k = 0 Или k = n Тогда
Возврат 1;
Иначе
Возврат Факториал(n) / (Факториал(k) * Факториал(n - k));
КонецЕсли;
КонецФункции
//////////////////
Метод оптимизированный: в обработке.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.13.82
Вступайте в нашу телеграмм-группу Инфостарт