Алгоритм сортировки, предложенный Дональдом Кнутом, представляет собой элегантный и эффективный метод упорядочивания данных, занимающий достойное место в обширном мире алгоритмов. В отличие от многих других алгоритмов сортировки, которые базируются на прямом сравнении элементов и обмене их местами, подход Кнута основан на построении специальной структуры данных, позволяющей эффективно находить место для каждого нового элемента в уже упорядоченной последовательности. Этот алгоритм, получивший название "сортировка деревом", использует двоичное дерево поиска в качестве основного инструмента для достижения поставленной цели. Двоичное дерево поиска – это древовидная структура данных, в которой каждый узел имеет не более двух потомков, называемых левым и правым поддеревьями. При этом, для каждого узла дерева выполняется важное свойство: все значения в левом поддереве меньше значения в узле, а все значения в правом поддереве больше значения в узле. Благодаря этому свойству, поиск элемента в двоичном дереве поиска может быть выполнен очень быстро, поскольку на каждом шаге поиска мы можем отбросить половину дерева, в которой заведомо не может находиться искомый элемент.. Существует несколько способов обхода двоичного дерева, но наиболее подходящим для сортировки деревом является так называемый "inorder" обход. При inorder обходе сначала рекурсивно обходится левое поддерево, затем посещается сам узел, а затем рекурсивно обходится правое поддерево. В результате такого обхода, элементы дерева посещаются в порядке возрастания, что и дает нам отсортированную последовательность.
Дональд Эрвин Кнут, чье имя неразрывно связано с этим алгоритмом, является выдающейся фигурой в мире информатики, оказавшим огромное влияние на развитие этой науки. Его фундаментальный труд "Искусство программирования" (The Art of Computer Programming) является настольной книгой для многих поколений программистов и исследователей, а его вклад в разработку алгоритмов и теорию вычислительной сложности трудно переоценить. Кнут родился 10 января 1938 года в Милуоки, штат Висконсин. Уже в школьные годы он проявил необычайные способности к математике и музыке. В 1963 году он получил степень доктора философии по математике в Калифорнийском технологическом институте, а затем начал свою преподавательскую деятельность в этом же университете. В 1968 году Кнут перешел в Стэнфордский университет, где и проработал профессором информатики до выхода на пенсию в 1993 году. Однако, и после выхода на пенсию, Кнут продолжает активно заниматься научной деятельностью, оставаясь одним из самых авторитетных и уважаемых ученых в своей области. Помимо "Искусства программирования", Кнут является автором множества научных статей и других книг, посвященных различным аспектам информатики. Он также известен своим вниманием к деталям и стремлением к совершенству, что проявляется во всех его работах. В частности, Кнут разработал собственную систему типографии TeX, которая стала стандартом де-факто для набора научных текстов, особенно в области математики и информатики. TeX позволяет создавать документы с высоким качеством оформления, что особенно важно для сложных математических выражений и формул. Любовь Кнута к деталям и стремление к совершенству проявляется и в его отношении к собственному труду "Искусство программирования". Он постоянно вносит исправления и дополнения в текст книги, стремясь сделать ее еще более полной и точной. Кнут даже учредил специальный денежный приз для тех, кто обнаружит ошибки в его книгах, что свидетельствует о его высочайшей ответственности перед читателями.
История возникновения алгоритма сортировки деревом тесно связана с развитием теории деревьев поиска и необходимостью эффективной организации данных. Идея использования двоичного дерева поиска для сортировки данных возникла достаточно давно, и ее корни можно проследить до работ, посвященных построению и анализу деревьев поиска. Однако, Дональд Кнут внес значительный вклад в популяризацию и анализ этого алгоритма, подробно описав его в своем фундаментальном труде "Искусство программирования". Кнут не только представил алгоритм сортировки деревом, но и провел его тщательный анализ, оценив его временную и пространственную сложность, а также сравнив его с другими алгоритмами сортировки. Благодаря его работе, сортировка деревом получила широкое распространение и стала одним из основных инструментов в арсенале программистов. Важно отметить, что Кнут рассматривал сортировку деревом не только как самостоятельный алгоритм, но и как иллюстрацию общих принципов построения и анализа алгоритмов. Он подчеркивал важность понимания основных концепций, лежащих в основе алгоритма, а не просто запоминания его кода. Такой подход позволяет программистам адаптировать алгоритм к конкретным задачам и эффективно использовать его в различных ситуациях. Кроме того, Кнут обращал внимание на практические аспекты реализации алгоритма, рассматривая различные способы представления деревьев поиска и методы оптимизации кода. Его рекомендации по реализации сортировки деревом до сих пор остаются актуальными и полезными для программистов, стремящихся к созданию эффективного и надежного программного обеспечения. Сортировка деревом, благодаря своим свойствам, нашла широкое применение в различных областях информатики. Она используется для организации данных в базах данных, для построения индексов, для реализации алгоритмов поиска и для решения других задач, требующих эффективного упорядочивания информации.
Дональд Кнут является автором множества других алгоритмов и концепций, оказавших значительное влияние на развитие информатики. Одним из наиболее известных его изобретений является алгоритм Кнута-Морриса-Пратта (KMP), который представляет собой эффективный алгоритм поиска подстроки в строке. В отличие от наивного алгоритма поиска, который сравнивает подстроку с каждым возможным положением в строке, алгоритм KMP использует информацию о структуре подстроки, чтобы избежать повторных сравнений. Это позволяет значительно ускорить процесс поиска, особенно в случаях, когда подстрока содержит повторяющиеся фрагменты. Алгоритм KMP широко используется в текстовых редакторах, поисковых системах и других приложениях, работающих с текстом. Еще одним важным вкладом Кнута является разработка системы LR-анализаторов, используемых для синтаксического анализа языков программирования. LR-анализаторы позволяют эффективно проверять, соответствует ли программа грамматике языка, и строить синтаксическое дерево программы. Эта технология является основой для многих компиляторов и интерпретаторов языков программирования. Кроме того, Кнут внес значительный вклад в теорию вычислительной сложности, занимаясь исследованием асимптотического поведения алгоритмов и развития этой науки, а также биографиям выдающихся ученых, внесших вклад в ее развитие. Его интерес к истории позволяет ему видеть современные проблемы в более широком контексте и находить решения, основанные на опыте прошлых поколений. В целом, вклад Дональда Кнута в информатику огромен и многогранен. Он является не только талантливым ученым и изобретателем, но и выдающимся педагогом и популяризатором науки. Его работы оказали огромное влияние на развитие информатики и продолжают вдохновлять новые поколения программистов и исследователей.
Логика основной процедуры. Для каждого элемента выполняется поиск места в дереве, куда его необходимо вставить. Поиск начинается с корня дерева и продолжается до тех пор, пока не будет найден подходящий пустой узел. Если значение текущего элемента меньше значения узла, то поиск продолжается в левом поддереве, в противном случае – в правом поддереве. Когда достигнут пустой узел, новый элемент вставляется в этот узел. Важно отметить, что при вставке элемента в дерево, необходимо поддерживать свойство двоичного дерева поиска, чтобы обеспечить правильность работы алгоритма. Это означает, что все элементы в левом поддереве должны быть меньше значения узла, а все элементы в правом поддереве должны быть больше значения узла. После того, как все элементы входной последовательности вставлены в дерево, необходимо выполнить обход дерева для получения отсортированной последовательности. Как уже упоминалось, наиболее подходящим способом обхода для сортировки деревом является inorder обход. При inorder обходе сначала рекурсивно обходится левое поддерево, затем посещается сам узел, а затем рекурсивно обходится правое поддерево. В результате такого обхода, элементы дерева посещаются в порядке возрастания, что и дает нам отсортированную последовательность. Для более глубокого понимания логики работы алгоритма, рассмотрим пример его работы на конкретной входной последовательности. Предположим, что нам необходимо отсортировать следующую последовательность чисел: 5, 2, 8, 1, 9, 4, 6, 3, 7. Сначала создается пустое двоичное дерево поиска. Затем последовательно обрабатываются элементы входной последовательности. Первый элемент – 5 – вставляется в корень дерева. Второй элемент – 2 – меньше 5, поэтому он вставляется в левое поддерево. Третий элемент – 8 – больше 5, поэтому он вставляется в правое поддерево. Четвертый элемент – 1 – меньше 5 и меньше 2, поэтому он вставляется в левое поддерево узла 2. И так далее. После вставки всех элементов, дерево будет иметь определенную структуру, отражающую упорядоченность элементов. Затем выполняется inorder обход полученного дерева. В результате обхода, элементы дерева будут посещены в следующем порядке: 1, 2, 3, 4, 5, 6, 7, 8, 9, что и является отсортированной последовательностью. Таким образом, алгоритм сортировки деревом позволяет эффективно упорядочивать данные, используя двоичное дерево поиска в качестве основной структуры данных. Простота логики и эффективность работы делают этот алгоритм одним из наиболее популярных и востребованных в различных областях информатики.
Напишем две реализации сортировки Кнута на 1С 8.3 :
1.
&НаСервере
Функция СортировкаКнута(МассивДляСортировки)
// Создаем копию массива, чтобы не изменять исходный
МассивДляСортировкиКопия = Новый Массив;
Для каждого Элемент из МассивДляСортировки Цикл
МассивДляСортировкиКопия.Добавить(Элемент);
КонецЦикла;
РазмерМассива = МассивДляСортировкиКопия.Количество();
// 1. Инициализация шага (фактор уменьшения = 1.2473309501)
Шаг = РазмерМассива;
ФакторУменьшения = 1.2473309501;
// 2. Пока шаг больше 1 или массив не отсортирован
Отсортировано = Ложь; // <--- Определяем переменную Отсортировано
Пока Шаг > 1 или Отсортировано = Ложь Цикл
// 3. Уменьшаем шаг
Шаг = Цел(Шаг / ФакторУменьшения);
Если Шаг < 1 Тогда
Шаг = 1;
КонецЕсли;
// Предполагаем, что массив отсортирован на этой итерации
Отсортировано = Истина;
// 4. Проходим по массиву с текущим шагом
Для Индекс = 0 По РазмерМассива - Шаг - 1 Цикл
// 5. Сравниваем элементы, отстоящие друг от друга на величину шага
Если МассивДляСортировкиКопия[Индекс] > МассивДляСортировкиКопия[Индекс + Шаг] Тогда
// 6. Меняем элементы местами
ВременнаяПеременная = МассивДляСортировкиКопия[Индекс];
МассивДляСортировкиКопия[Индекс] = МассивДляСортировкиКопия[Индекс + Шаг];
МассивДляСортировкиКопия[Индекс + Шаг] = ВременнаяПеременная;
// Если была перестановка, то массив не отсортирован
Отсортировано = Ложь;
КонецЕсли;
КонецЦикла;
КонецЦикла;
Возврат МассивДляСортировкиКопия;
КонецФункции
Данный программный фрагмент реализует алгоритм сортировки, предназначенный для упорядочивания элементов в массиве. Этот алгоритм является усовершенствованной версией классической сортировки обменами, стремящейся повысить её эффективность за счет уменьшения количества сравнений и перемещений элементов.
В начале работы создается копия исходного массива, что позволяет избежать изменения порядка элементов в оригинальной структуре данных. Это обеспечивает сохранность исходной информации и позволяет использовать функцию сортировки без опасений о её побочных эффектах. Далее определяется количество элементов в массиве, что необходимо для организации циклов и управления процессом сортировки.
Ключевой особенностью алгоритма является использование переменного шага, который постепенно уменьшается в процессе работы. Изначально шаг устанавливается равным размеру массива, что позволяет сравнивать элементы, находящиеся на значительном расстоянии друг от друга. Затем шаг уменьшается с использованием специального коэффициента, который, как считается, обеспечивает оптимальную скорость сходимости алгоритма. Уменьшение шага продолжается до тех пор, пока он не станет равен единице.
Основной цикл алгоритма выполняется до тех пор, пока шаг больше единицы или пока не будет установлено, что массив полностью отсортирован. На каждой итерации цикла шаг уменьшается, и выполняется проход по массиву с текущим значением шага. В процессе прохода сравниваются элементы, отстоящие друг от друга на величину шага. Если оказывается, что элементы расположены в неправильном порядке, они меняются местами.
Факт перестановки элементов является индикатором того, что массив еще не отсортирован. Если на какой-либо итерации цикла не было выполнено ни одной перестановки, это означает, что все элементы, отстоящие друг от друга на текущий шаг, расположены в правильном порядке. В этом случае можно предположить, что массив близок к отсортированному состоянию, и алгоритм может завершить свою работу.
После завершения основного цикла алгоритма возвращается отсортированная копия массива. Использование копии, как уже отмечалось, гарантирует неизменность исходных данных и повышает гибкость применения функции сортировки в различных программных контекстах.
Эффективность данного алгоритма сортировки обусловлена несколькими факторами. Во-первых, использование переменного шага позволяет быстро перемещать элементы на большие расстояния, что особенно полезно для массивов, в которых элементы изначально сильно перемешаны. Во-вторых, адаптивный характер алгоритма, заключающийся в проверке отсортированности массива на каждой итерации, позволяет избежать лишних проходов и сократить общее время работы. В-третьих, сравнительно простой код алгоритма облегчает его понимание, отладку и модификацию.
2.
&НаСервере
Функция СортировкаШелла(МассивДляСортировки)
//Алгоритм Шелла (Кнута)
// Создаем копию массива, чтобы не изменять исходный
МассивДляСортировкиКопия = Новый Массив;
Для каждого Элемент из МассивДляСортировки Цикл
МассивДляСортировкиКопия.Добавить(Элемент);
КонецЦикла;
РазмерМассива = МассивДляСортировкиКопия.Количество();
// Шаг 1: Инициализация шага (gap)
Шаг = Цел(РазмерМассива / 2);
// Шаг 2: Цикл по шагам
Пока Шаг > 0 Цикл
// Шаг 3: Цикл по элементам внутри каждого шага
Для Индекс = Шаг По РазмерМассива - 1 Цикл
// Шаг 4: Вставка элемента в отсортированную подпоследовательность
Значение = МассивДляСортировкиКопия[Индекс];
ИндексВставки = Индекс;
// Шаг 5: Сдвигаем элементы, пока не найдем место для вставки
Пока ИндексВставки >= Шаг И МассивДляСортировкиКопия[ИндексВставки - Шаг] > Значение Цикл
МассивДляСортировкиКопия[ИндексВставки] = МассивДляСортировкиКопия[ИндексВставки - Шаг];
ИндексВставки = ИндексВставки - Шаг;
КонецЦикла;
// Шаг 6: Вставляем элемент
МассивДляСортировкиКопия[ИндексВставки] = Значение;
КонецЦикла;
// Шаг 7: Уменьшаем шаг
Шаг = Цел(Шаг / 2);
КонецЦикла;
Возврат МассивДляСортировкиКопия;
КонецФункции
В мире алгоритмов сортировки существует множество подходов, каждый из которых обладает своими уникальными характеристиками и эффективностью в различных сценариях. Одним из таких методов, заслуживающих внимания, является алгоритм Шелла, иногда называемый алгоритмом Кнута, названный в честь Дональда Кнута, внесшего значительный вклад в его анализ и оптимизацию. Этот алгоритм представляет собой усовершенствованную версию сортировки вставками, позволяющую значительно повысить её производительность за счет уменьшения количества перемещений элементов на большие расстояния.
Основная идея, лежащая в основе алгоритма Шелла, заключается в разделении исходного массива на несколько подмассивов, элементы которых отстоят друг от друга на определенное расстояние, называемое шагом. Каждый из этих подмассивов сортируется с использованием сортировки вставками. За счет этого, элементы, находящиеся далеко друг от друга в исходном массиве, могут быстрее переместиться на свои правильные позиции. По мере выполнения алгоритма, шаг постепенно уменьшается, и подмассивы становятся все более крупными, пока, наконец, не будет выполнен один проход сортировки вставками по всему массиву.
Разберем этот процесс более детально. Пер шаг не станет равным нулю.
Внутри основного цикла происходит итерация по элементам массива, начиная с позиции, равной шагу. Для каждого элемента выполняется вставка в отсортированную подпоследовательность, расположенную на расстоянии, кратном шагу. Это означает, что текущий элемент сравнивается с элементами, находящимися на расстоянии шага слева от него, и, если необходимо, перемещается на свою правильную позицию путем сдвига элементов вправо.
Процесс вставки элемента в отсортированную подпоследовательность аналогичен сортировке вставками. Текущий элемент сохраняется во временной переменной, а затем сравнивается с элементами, расположенными слева от него на расстоянии шага. Если текущий элемент меньше, чем элемент слева, то элемент слева сдвигается на одну позицию вправо, и процесс сравнения продолжается. Когда находится элемент, который меньше или равен текущему элементу, или когда достигается начало подпоследовательности, текущий элемент вставляется на освободившееся место.
После завершения цикла по элементам для текущего значения шага, значение шага уменьшается вдвое. Это приводит к тому, что на следующем проходе алгоритма будут сортироваться более крупные подмассивы, и элементы будут перемещаться на меньшие расстояния. Когда шаг становится равным единице, выполняется обычная сортировка вставками по всему массиву, что гарантирует полную сортировку массива.
Алгоритм Шелла является более эффективным, чем обычная сортировка вставками, особенно для массивов большого размера. Это связано с тем, что он позволяет элементам перемещаться на большие расстояния на ранних стадиях алгоритма, что значительно уменьшает количество перемещений, необходимых на поздних стадиях. Однако, алгоритм Шелла не является самым быстрым алгоритмом сортировки. Существуют более сложные алгоритмы, такие как сортировка слиянием и быстрая сортировка, которые обладают более высокой производительностью в среднем случае.
Одним из ключевых факторов, влияющих на производительность алгоритма Шелла, является выбор последовательности шагов. Различные последовательности шагов могут приводить к разной эффективности алгоритма. Последовательность, используемая в приведенном примере (деление шага пополам на каждом проходе), является достаточно простой, но не всегда оптимальной. Существуют более сложные последовательности шагов, которые могут улучшить производительность алгоритма.
Несмотря на то, что алгоритм Шелла не является самым быстрым алгоритмом сортировки, он обладает рядом преимуществ. Он относительно прост в реализации, не требует дополнительной памяти (в отличие от сортировки слиянием) и хорошо работает на массивах умеренного размера. Поэтому, алгоритм Шелла может быть полезным инструментом в тех случаях, когда требуется быстрая и простая реализация сортировки, а размер массива не слишком велик.
Таким образом, алгоритм Шелла представляет собой ценный инструмент в арсенале разработчика, предлагающий эффективный способ сортировки массивов с использованием принципа уменьшающегося шага. Его простота и относительная скорость делают его подходящим выбором для различных задач, особенно когда требуется компромисс между производительностью и легкостью реализации.
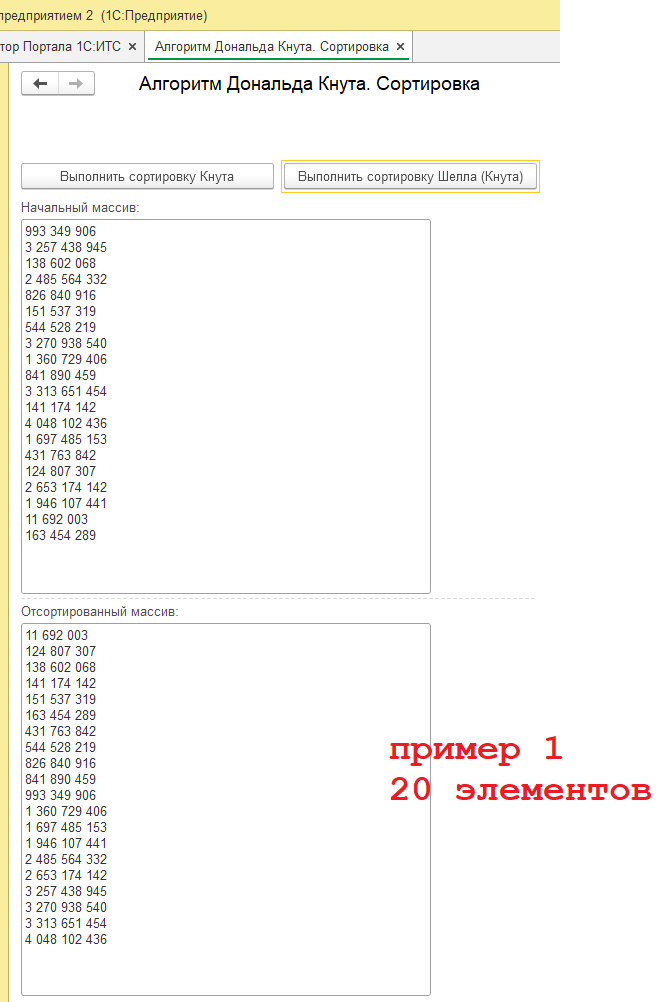
Итак, мы рассмотрели два примера сортировки. Приведенные коды работоспособны, и вы можете использовать их из статьи или воспользоваться готовой обработкой, демонстрирующей результаты работы этих алгоритмов сортировки. Описание и код рассчитаны для начинающих программистов, код обработки открыт.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.13.82
Вступайте в нашу телеграмм-группу Инфостарт