Хеш-поиск с использованием хеш-таблицы и разрешением коллизий методом цепочек: Глубокое погружение

Хеш-поиск с использованием хеш-таблицы и разрешением коллизий методом цепочек: Глубокое погружение

Часть 1: Зарождение концепции и определение хеш-поиска

       В бескрайнем океане информации, где каждый элемент стремится затеряться в хаотичном беспорядке, возникает насущная потребность в эффективных методах поиска. Представьте себе необъятную библиотеку, в которой книги расставлены без всякой системы, в случайном порядке. Поиск нужной книги в такой библиотеке превратится в кошмарную задачу, требующую колоссальных затрат времени и усилий. Именно в таких условиях рождается необходимость в структурах данных и алгоритмах, способных организовать информацию таким образом, чтобы поиск нужного элемента занимал минимальное время. Одним из таких выдающихся решений является хеш-поиск, метод, позволяющий находить элементы в огромных массивах данных практически мгновенно. Но как же устроен этот волшебный инструмент, позволяющий преодолевать кажущийся непреодолимым барьер сложности?

      Хеш-поиск, в своей сущности, представляет собой метод поиска данных, основанный на использовании хеш-функции для преобразования ключа поиска в индекс, указывающий на местоположение элемента в хеш-таблице. Хеш-таблица, в свою очередь, является структурой данных, реализующей интерфейс ассоциативного массива, то есть позволяющей хранить пары “ключ-значение” и осуществлять быстрый поиск значения по заданному ключу. Основная идея хеш-поиска заключается в том, чтобы, зная ключ, вычислить его хеш-код с помощью хеш-функции и использовать этот хеш-код в качестве индекса в хеш-таблице. В идеальном случае, каждому ключу соответствует уникальный индекс, и поиск нужного элемента сводится к простому обращению к ячейке таблицы по этому индексу. Однако, в реальном мире, добиться такой идеальной ситуации практически невозможно. Количество возможных ключей обычно значительно превосходит размер хеш-таблицы, что приводит к возникновению коллизий – ситуаций, когда разные ключи отображаются в один и тот же индекс.

       Разрешение коллизий является ключевым аспектом реализации хеш-поиска. Существует множество методов разрешения коллизий, каждый из которых имеет свои преимущества и недостатки. Одним из наиболее распространенных и элегантных методов является метод цепочек, также известный как раздельное связывание. В этом методе каждая ячейка хеш-таблицы содержит не отдельный элемент, а указатель на связный список, содержащий все элементы, ключи которых отображаются в данный индекс. Таким образом, при возникновении коллизии, новый элемент просто добавляется в соответствующий связный список. При поиске элемента сначала вычисляется его хеш-код, затем происходит переход к соответствующему связному списку, и, наконец, осуществляется последовательный поиск нужного элемента в этом списке.

      Хеш-поиск с использованием хеш-таблицы и разрешением коллизий методом цепочек представляет собой мощный и гибкий инструмент, сочетающий в себе простоту реализации и высокую производительность. Он позволяет достигать в среднем константного времени поиска, что делает его незаменимым во многих приложениях, требующих быстрого доступа к данным. Однако, эффективность хеш-поиска во многом зависит от выбора хеш-функции и от распределения ключей. Неудачный выбор хеш-функции может привести к неравномерному распределению ключей по хеш-таблице, что, в свою очередь, приведет к увеличению длины связных списков и снижению производительности поиска. В наихудшем случае, когда все ключи отображаются в один и тот же индекс, время поиска деградирует до линейного времени, как в обычном связном списке. Поэтому, при проектировании системы хеш-поиска необходимо уделять особое внимание выбору хеш-функции и методам борьбы с неравномерным распределением ключей.

Часть 2: Исторические корни и пионеры хеш-поиска

      История хеш-поиска уходит корнями в далекое прошлое, когда люди впервые столкнулись с необходимостью организации больших объемов информации. Хотя точное время и имя изобретателя хеш-таблиц установить невозможно, первые зачатки этой концепции можно увидеть в древних системах классификации и индексации. В частности, древние библиотеки и архивы использовали различные методы для организации книг и документов, позволяющие быстро находить нужную информацию. Эти методы, хотя и не использовали математические функции для вычисления индексов, концептуально предвосхищали идею хеш-поиска.

       В современном виде, хеш-поиск начал формироваться в середине XX века, с развитием компьютерной техники и появлением первых баз данных. Одним из пионеров в этой области был Ханс Питер Лун, сотрудник IBM, который в 1953 году предложил использовать хеш-функцию для быстрого поиска слов в текстовых документах. Его идея заключалась в том, чтобы преобразовать каждое слово в числовой код с помощью хеш-функции и использовать этот код в качестве индекса в таблице, содержащей указатели на соответствующие документы. Этот метод позволил значительно ускорить поиск информации в текстовых базах данных и стал одним из первых применений хеш-поиска в компьютерной сфере.

      Другим важным вкладом в развитие хеш-поиска стала работа Арнольда Думи в 1956 году. Думи предложил использовать хеш-таблицы для реализации символьных таблиц в компиляторах. Символьная таблица – это структура данных, используемая компилятором для хранения информации о переменных, функциях и других идентификаторах, используемых в программе. Думи показал, что использование хеш-таблиц позволяет значительно ускорить поиск информации в символьной таблице, что, в свою очередь, приводит к ускорению компиляции программы. Его работа оказала огромное влияние на развитие компиляторов и стала одним из ключевых факторов, способствовавших распространению хеш-поиска в программном обеспечении.

      Несмотря на то, что первые хеш-функции были достаточно простыми и примитивными, они продемонстрировали огромный потенциал хеш-поиска для ускорения доступа к данным. В последующие годы, исследователи и разработчики сосредоточились на разработке более эффективных хеш-функций и методов разрешения коллизий. Были предложены различные методы разрешения коллизий, такие как линейное пробирование, квадратичное пробирование и двойное хеширование, каждый из которых имел свои преимущества и недостатки. Однако, метод цепочек, предложенный независимо несколькими исследователями, оказался наиболее универсальным и гибким, и стал одним из самых популярных методов разрешения коллизий в хеш-таблицах.

      Развитие хеш-поиска неразрывно связано с развитием баз данных. В 1970-х годах, с появлением реляционных баз данных, хеш-таблицы стали широко использоваться для реализации индексов, позволяющих ускорить поиск данных в таблицах базы данных. Индексы на основе хеш-таблиц позволяют находить нужные строки в таблице по значению определенных столбцов практически мгновенно, что значительно повышает производительность баз данных. Сегодня, хеш-таблицы являются неотъемлемой частью современных баз данных и используются для реализации различных видов индексов, а также для кэширования данных и других целей.

      История хеш-поиска – это история непрерывного развития и совершенствования, направленного на повышение производительности и эффективности поиска данных. От первых примитивных хеш-функций до современных сложных алгоритмов, хеш-поиск прошел долгий путь и стал одним из самых востребованных инструментов в арсенале программиста. Его применение охватывает самые разные области, от баз данных и компиляторов до сетевых протоколов и криптографии, что свидетельствует о его универсальности и важности для современной информатики.

Часть 3: Математические основы и анализ хеш-поиска

       Эффективность хеш-поиска зиждется на прочном фундаменте математических концепций и аналитических методов. Понимание математических основ позволяет не только глубже проникнуть в суть алгоритма, но и принимать обоснованные решения при выборе хеш-функции, метода разрешения коллизий и размера хеш-таблицы. В основе хеш-поиска лежит понятие хеш-функции, математической функции, преобразующей ключ поиска в индекс. Хеш-функция должна удовлетворять нескольким важным требованиям: она должна быть детерминированной, то есть для одного и того же ключа она всегда должна возвращать один и тот же индекс; она должна быть вычислительно эффективной, то есть вычисление хеш-кода должно занимать минимальное время; и, самое главное, она должна равномерно распределять ключи по хеш-таблице, чтобы минимизировать количество коллизий.

        Создание идеальной хеш-функции, удовлетворяющей всем этим требованиям, является сложной задачей. На практике, хеш-функции часто разрабатываются с учетом особенностей конкретных данных и приложений. Существует множество различных типов хеш-функций, каждая из которых имеет свои преимущества и недостатки. Одними из наиболее распространенных типов хеш-функций являются хеш-функции на основе полиномов, хеш-функции на основе умножения и хеш-функции на основе криптографических алгоритмов. Хеш-функции на основе полиномов вычисляют хеш-код как значение полинома, коэффициенты которого зависят от символов ключа. Хеш-функции на основе умножения умножают ключ на константу и используют определенные биты результата в качестве хеш-кода. Хеш-функции на основе криптографических алгоритмов используют криптографические хеш-функции, такие как MD5 или SHA-1, для вычисления хеш-кода.

       Помимо выбора хеш-функции, важным аспектом является анализ ее производительности и равномерности распределения ключей. Для оценки качества хеш-функции используются различные статистические метрики, такие как коэффициент коллизий, дисперсия распределения ключей и энтропия. Коэффициент коллизий показывает, какая доля ключей отображается в один и тот же индекс. Дисперсия распределения ключей показывает, насколько равномерно распределены ключи по хеш-таблице. Энтропия показывает, насколько непредсказуемым является хеш-код, что является важным для безопасности хеш-таблицы.

      Анализ хеш-поиска также включает в себя оценку его временной сложности. Временная сложность алгоритма показывает, как время выполнения алгоритма зависит от размера входных данных. В идеальном случае, время поиска элемента в хеш-таблице должно быть константным, то есть не зависеть от количества элементов в таблице. Однако, из-за наличия коллизий, время поиска может варьироваться. В случае использования метода цепочек для разрешения коллизий, среднее время поиска элемента в хеш-таблице составляет O(1 + α), где α – коэффициент загрузки хеш-таблицы, равный отношению количества элементов в таблице к ее размеру. Если коэффициент загрузки невелик, то время поиска практически не зависит от количества элементов в таблице и приближается к константному времени. Однако, если коэффициент загрузки велик, то время поиска увеличивается пропорционально коэффициенту загрузки.

       В наихудшем случае, когда все ключи отображаются в один и тот же индекс, время поиска деградирует до O(n), где n – количество элементов в хеш-таблице. Это происходит, когда хеш-функция возвращает одинаковый хеш-код для всех ключей, или когда используется неудачный метод разрешения коллизий, приводящий к образованию длинных цепочек. Чтобы избежать таких ситуаций, необходимо тщательно выбирать хеш-функцию и метод разрешения коллизий, а также поддерживать коэффициент загрузки хеш-таблицы на разумном уровне.

       Математический анализ хеш-поиска позволяет не только оценить его производительность, но и оптимизировать его параметры. Зная особенности данных и требования к производительности, можно выбрать наиболее подходящую хеш-функцию, метод разрешения коллизий и размер хеш-таблицы, чтобы обеспечить оптимальное время поиска и минимальное использование памяти. В частности, можно использовать динамическое изменение размера хеш-таблицы для поддержания коэффициента загрузки на заданном уровне. При увеличении коэффициента загрузки, размер таблицы увеличивается, а элементы перехешируются, чтобы равномерно распределить их по новой таблице. При уменьшении коэффициента загрузки, размер таблицы уменьшается, чтобы сэкономить память.

     Математика является незаменимым инструментом для понимания и оптимизации хеш-поиска. Зная математические основы алгоритма, можно разрабатывать более эффективные и надежные системы хранения и поиска данных, способные справляться с огромными объемами информации и удовлетворять самым высоким требованиям к производительности.

Часть 4: Сравнение с другими методами поиска и их особенности

       Хеш-поиск, несмотря на свои очевидные преимущества, не является единственным методом поиска данных. Существуют и другие методы, каждый из которых имеет свои сильные и слабые стороны и подходит для решения определенных задач. Сравнение хеш-поиска с другими методами позволяет лучше пор, пока не будет найден нужный элемент. Временная сложность линейного поиска составляет O(n), где n – количество элементов в массиве. Это означает, что время поиска увеличивается пропорционально количеству элементов. Линейный поиск подходит для небольших массивов данных, или когда необходимо найти элемент, который находится в начале массива. Однако, для больших массивов данных, линейный поиск становится крайне неэффективным.

       Бинарный поиск – это более эффективный метод поиска, используемый для поиска элементов в отсортированном массиве. Бинарный поиск заключается в разделении массива пополам и сравнении среднего элемента с ключом поиска. Если средний элемент равен ключу поиска, то элемент найден. Если средний элемент больше ключа поиска, то поиск продолжается в левой половине массива. Если средний элемент меньше ключа поиска, то поиск продолжается в правой половине массива. Этот процесс повторяется до тех пор, пока не будет найден нужный элемент, или пока не будет доказано, что элемент в массиве отсутствует. Временная сложность бинарного поиска составляет O(log n), где n – количество элементов в массиве. Это означает, что время поиска увеличивается логарифмически с увеличением количества элементов. Бинарное дерево поиска – это структура данных, в которой каждый узел имеет ключ и указатели на левого и правого потомка. Левый потомок содержит ключ, меньший, чем ключ текущего узла, а правый потомок содержит ключ, больший, чем ключ текущего узла. Поиск элемента в дереве поиска начинается с корневого узла и продолжается до тех пор, пока не будет найден нужный элемент, или пока не будет достигнут лист дерева. Временная сложность поиска в сбалансированном дереве поиска составляет O(log n), где n – количество узлов в дереве. Деревья поиска позволяют не только быстро находить элементы, но и осуществлять другие операции, такие как вставка, удаление и сортировка элементов. Однако, деревья поиска требуют больших затрат памяти, чем массивы, и могут быть сложными в реализации.

       В отличие от этих методов, хеш-поиск стремится достичь константного времени поиска, не зависящего от количества элементов в таблице. В среднем, время поиска элемента в хеш-таблице составляет O(1), что делает хеш-поиск самым быстрым методом поиска. Однако, в наихудшем случае, время поиска может деградировать до O(n), как в линейном поиске. Хеш-поиск требует больших затрат памяти, чем линейный и бинарный поиск, но может быть более экономичным, чем поиск с использованием деревьев поиска.

      Выбор метода поиска зависит от конкретных требований задачи. Если необходимо найти элемент в небольшом неотсортированном массиве, то линейный поиск может быть самым простым и эффективным решением. Если необходимо многократно искать элементы в отсортированном массиве, то бинарный поиск будет более подходящим. Если необходимо не только искать элементы, но и вставлять, удалять и сортировать их, то поиск с использованием деревьев поиска может быть оптимальным. Если необходимо максимально ускорить поиск, даже в ущерб памяти и стабильности, то хеш-поиск будет лучшим выбором.

        Хеш-поиск особенно эффективен в тех случаях, когда необходимо реализовать ассоциативный массив, то есть структуру данных, позволяющую хранить пары “ключ-значение” и осуществлять быстрый поиск значения по заданному ключу. Ассоциативные массивы широко используются в различных приложениях, таких как кэширование данных, индексирование баз данных, реализация символьных таблиц в компиляторах и т.д. В этих приложениях, высокая скорость поиска является критически важной, и хеш-поиск является незаменимым инструментом.

      В заключение, выбор метода поиска – это компромисс между временем поиска, использованием памяти и сложностью реализации. Хеш-поиск, благодаря своей способности достигать константного времени поиска, является одним из самых востребованных методов поиска данных, особенно в приложениях, требующих высокой производительности и частого доступа к данным.

Часть 5: Применимость хеш-поиска в "1С:Предприятие" и его перспективы

"1С:Предприятие" – это платформа для разработки и автоматизации бизнес-приложений, широко используемая в различных организациях для управления учетом, финансами, торговлей и другими бизнес-процессами. В “1С:Предприятие” часто возникает необходимость в быстром поиске данных, например, при поиске контрагентов по ИНН, товаров по артикулу или документов по номеру. В этих ситуациях, хеш-поиск может стать эффективным инструментом для ускорения доступа к данным и повышения производительности приложений.

       Встроенный язык "1С:Предприятие" предоставляет возможности для реализации хеш-поиска с использованием хеш-таблиц и разрешением коллизий методом цепочек. Можно создать пользовательскую структуру данных, реализующую интерфейс ассоциативного массива, и использовать ее для хранения и поиска данных. Для вычисления хеш-кодов можно использовать различные встроенные функции, такие как функция "ХешСтроки" или функцию “MD5”, или разработать собственные хеш-функции, учитывающие особенности данных.

      Однако, следует учитывать, что встроенный язык "1С:Предприятие" имеет некоторые ограничения, которые могут повлиять на производительность хеш-поиска. В частности, встроенный язык является интерпретируемым, что может замедлить выполнение некоторых операций, таких как вычисление хеш-кодов и поиск элементов в связных списках. Кроме того, встроенный язык не предоставляет прямых средств для управления памятью, что может привести к неэффективному использованию памяти при работе с большими объемами данных.

       Несмотря на эти ограничения, хеш-поиск может быть успешно применен в "1С:Предприятие" для решения различных задач. Например, можно использовать хеш-таблицы для кэширования данных, часто используемых в приложениях. Кэширование данных позволяет избежать повторных обращений к базе данных, что значительно ускоряет работу приложений. Также, можно использовать хеш-таблицы для индексирования данных в регистрах сведений и других объектах метаданных. Индексы на основе хеш-таблиц позволяют ускорить поиск данных по определенным измерениям, что повышает производительность отчетов и других аналитических инструментов.

       Для повышения производительности хеш-поиска в "1С:Предприятие" можно использовать различные методы с конкретными данными. Например, если ключами поиска являются строки, то можно использовать хеш-функции, разработанные специально для работы со строками.

      В будущем, можно ожидать дальнейшего развития хеш-поиска в "1С:Предприятие". С появлением новых версий платформы и расширением возможностей встроенного языка, станут доступны более эффективные средства для реализации хеш-таблиц и управления памятью. Также, можно ожидать появления специализированных библиотек и компонентов, реализующих различные алгоритмы хеш-поиска и предоставляющих удобный интерфейс для их использования в приложениях "1С:Предприятие".

      Хеш-поиск с использованием хеш-таблицы и разрешением коллизий методом цепочек – это мощный и перспективный инструмент, который может быть успешно применен в "1С:Предприятие" для ускорения доступа к данным и повышения производительности приложений. Несмотря на некоторые ограничения, связанные с особенностями платформы, хеш-поиск позволяет решать различные задачи, связанные с хранением и поиском данных, и может стать незаменимым помощником для разработчиков "1С:Предприятие". В дальнейшем, с развитием платформы и появлением новых инструментов, хеш-поиск получит еще большее распространение и станет неотъемлемой частью экосистемы "1С:Предприятие".

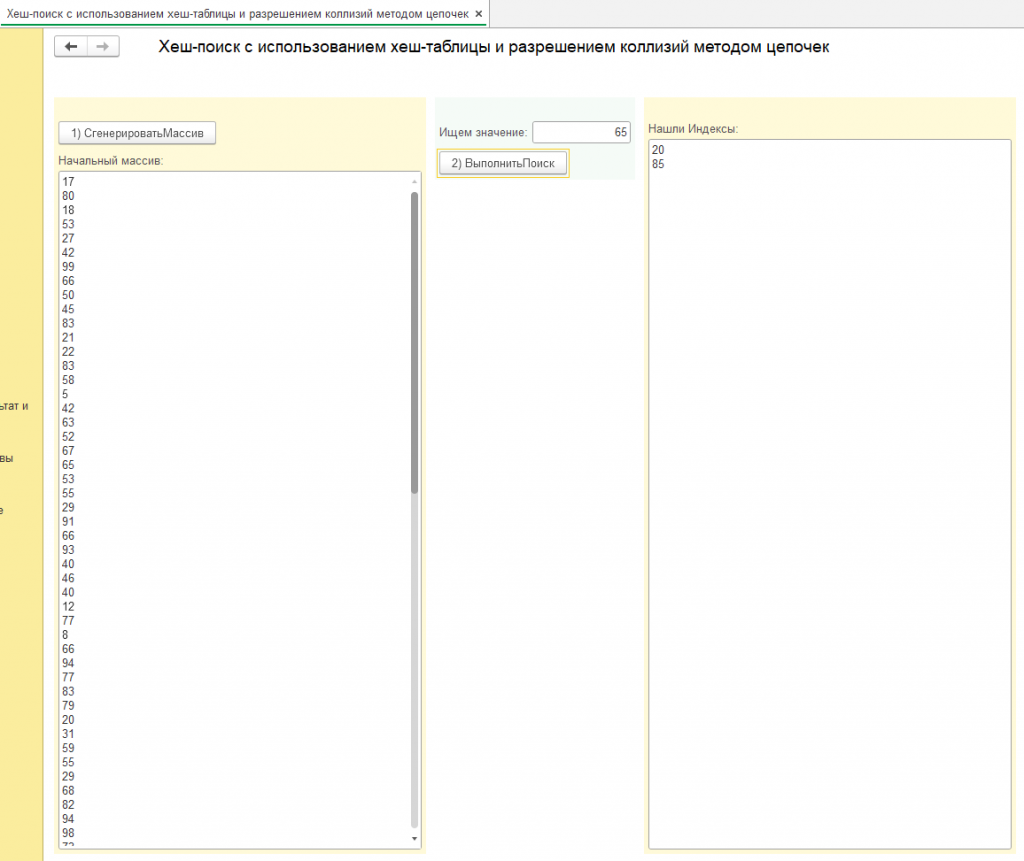
Внимание, на скриншотах для примера взят несортированный массив из 100 элементов, созданный генератором случайных чисел в диапазоне от 0 до 100 для наглядности. 

&НаСервере
Функция ХешПоиск(Массив, ИскомоеЗначение) Экспорт

    // 1. Создаем хеш-таблицу
    ХешТаблица = Новый Соответствие;
    Для Индекс = 0 По Массив.Количество() - 1 Цикл
        Элемент = Массив[Индекс];
        Хеш = ВычислитьХеш(Элемент);

        // Разрешение коллизий методом цепочек
        Если ХешТаблица.Получить(Хеш) <> Неопределено Тогда
            // Ключ уже существует, добавляем элемент в цепочку
            Если ТипЗнч(ХешТаблица[Хеш]) = Тип("Массив") Тогда
                ХешТаблица[Хеш].Добавить(Новый Структура("Значение, Индекс", Элемент, Индекс));
            Иначе
                // Если по ключу не массив, а структура, то сначала нужно преобразовать в массив
                ПрежняяСтруктура = ХешТаблица[Хеш];
                НовыйМассив = Новый Массив;
                НовыйМассив.Добавить(ПрежняяСтруктура);
                НовыйМассив.Добавить(Новый Структура("Значение, Индекс", Элемент, Индекс));
                ХешТаблица[Хеш] = НовыйМассив;
            КонецЕсли;
        Иначе
            // Ключа еще нет, создаем новую цепочку
            НоваяСтруктура = Новый Структура("Значение, Индекс", Элемент, Индекс);
            НовыйМассив = Новый Массив;
            НовыйМассив.Добавить(НоваяСтруктура);
            ХешТаблица.Вставить(Хеш, НовыйМассив);  // Вставляем МАССИВ, содержащий структуру
        КонецЕсли;
    КонецЦикла;

    // 2. Ищем искомое значение в хеш-таблице
    ИндексыВхождений = Новый Массив;
    ХешИскомого = ВычислитьХеш(ИскомоеЗначение);

    Если ХешТаблица.Получить(ХешИскомого) <> Неопределено Тогда
        // Ключ найден, просматриваем цепочку
        НайденныеЭлементы = ХешТаблица[ХешИскомого];

        Если ТипЗнч(НайденныеЭлементы) = Тип("Массив") Тогда
            Для Каждого Элемент Из НайденныеЭлементы Цикл
                Если Элемент.Значение = ИскомоеЗначение Тогда
                    ИндексыВхождений.Добавить(Элемент.Индекс);
                КонецЕсли;
            КонецЦикла;
        Иначе
            // Если по ключу не массив, а структура, то обрабатываем как единственный элемент
            Если НайденныеЭлементы.Значение = ИскомоеЗначение Тогда
                ИндексыВхождений.Добавить(НайденныеЭлементы.Индекс);
            КонецЕсли;
        КонецЕсли;

    КонецЕсли;

    Возврат ИндексыВхождений;

КонецФункции

// Вычисление хеша (простая реализация, можно заменить на более сложную)
&НаСервере
Функция ВычислитьХеш(Значение)

    СтрокаЗначения = Строка(Значение);
    Длина = СтрДлина(СтрокаЗначения);
    Хеш = 0;

    Для СимволПозиция = 1 По Длина Цикл
        КодСимвола = КодСимвола(Сред(СтрокаЗначения, СимволПозиция, 1));
        Хеш = Хеш * 31 + КодСимвола; // Простое хеширование с умножением и сложением
    КонецЦикла;

    Возврат Хеш;

КонецФункции


// Обработка коллизии методом кукушкиного хеширования
&НаСервере
Процедура ОбработатьКоллизию(ХешТаблица, Хеш, Элемент, Индекс)

    // Ограничиваем количество попыток, чтобы избежать бесконечного цикла
    МаксимальноеЧислоПопыток = 100;
    Попытка1 = 0;
	
    Пока ХешТаблица.СодержитКлюч(Хеш) И Попытка1 < МаксимальноеЧислоПопыток Цикл
        Попытка1 = Попытка1 + 1;

        // 1. Извлекаем существующий элемент из ячейки
        СуществующиеЭлементы = ХешТаблица[Хеш];
		
		Если ТипЗнч(СуществующиеЭлементы) <> Тип("Массив") Тогда
			
			Возврат;  // Если в ячейке что-то не то, выходим
			
		КонецЕсли;	
		
		Если СуществующиеЭлементы.Количество() = 0 Тогда
			
			ХешТаблица[Хеш].Добавить(Новый Структура("Значение, Индекс", Элемент, Индекс));
			
			Возврат;
			
		КонецЕсли;	

        СуществующийЭлемент = СуществующиеЭлементы[0];  // Берем первый элемент

        // 2. "Выбрасываем" существующий элемент, вычисляем для него новый хеш
        НовыйЭлемент = Новый Структура("Значение, Индекс", Элемент, Индекс);
        ХешТаблица[Хеш].Удалить(0);
        ХешТаблица[Хеш].Добавить(НовыйЭлемент);
		
        Элемент = СуществующийЭлемент.Значение;
        Индекс = СуществующийЭлемент.Индекс;
		
        Хеш = ВычислитьХеш(Элемент);

        // 3. Пытаемся вставить "выброшенный" элемент в новую ячейку
        Если Не ХешТаблица.СодержитКлюч(Хеш) Тогда
            ХешТаблица.Вставить(Хеш, Новый Массив);
            ХешТаблица[Хеш].Добавить(Новый Структура("Значение, Индекс", Элемент, Индекс));
            Возврат;
        КонецЕсли;

    КонецЦикла;

    Сообщить("Превышено максимальное количество попыток разрешения коллизии!");

КонецПроцедуры

       Представленный программный фрагмент реализует алгоритм поиска в массиве, основанный на принципе хеширования. Суть данного подхода заключается в преобразовании каждого элемента массива в уникальный числовой код, называемый хешем, который служит ключом для быстрого доступа к этому элементу. Для этого создается специальная структура данных, где каждому хешу соответствует список элементов, обладающих этим хешем. В процессе поиска, сначала вычисляется хеш искомого значения, а затем происходит обращение к хранилищу данных по этому хешу. Если по данному ключу обнаруживаются элементы, выполняется их последовательное сравнение с искомым значением.

      Важной особенностью реализации является механизм разрешения коллизий – ситуаций, когда разным элементам соответствуют одинаковые хеши. В данном случае используется метод цепочек, при котором элементы с одинаковыми хешами объединяются в списки, привязанные к соответствующему ключу.

      Алгоритм возвращает массив, содержащий индексы всех вхождений искомого значения в исходном массиве. Такой подход обеспечивает возможность обработки ситуаций, когда искомое значение встречается в массиве несколько раз. Данный алгоритм особенно эффективен для больших объемов данных, где требуется быстрый поиск информации, значительно превосходя по скорости традиционные методы последовательного перебора.