Алгоритм пропорционального распределения
Алгоритм пропорционального распределения, в своей базовой форме, – это один из самых интуитивно понятных и широко применяемых методов распределения ресурсов. Его суть заключается в разбиении некоторого общего ресурса между несколькими получателями пропорционально заданным весовым коэффициентам. Представьте, что у вас есть определённое количество денег, которые нужно распределить между несколькими отделами компании в зависимости от их вклада в общий результат. Простой алгоритм пропорционального распределения в этом случае будет заключаться в определении доли каждого отдела в общем результате и распределении денег пропорционально этим долям. Например, если отдел продаж обеспечил 60% общего дохода, то он получит 60% выделенного бюджета. Однако, базовый алгоритм часто не учитывает нюансы реальной ситуации, и именно поэтому требуется усложненный вариант, включающий поправочный коэффициент.
Этот поправочный коэффициент вносит существенные изменения в алгоритм, позволяя корректировать распределение ресурсов в зависимости от дополнительных факторов, не учтенных в базовых весовых коэффициентах. Это могут быть, например, срочность выполнения задачи, сложность проекта, наличие ограниченных ресурсов или особые потребности конкретного получателя. Введение поправочного коэффициента делает алгоритм более гибким и адаптируемым к разнообразным ситуациям. Без него, распределение ресурсов может быть несправедливым или неэффективным, если не все важные факторы учтены в базовых весовых коэффициентах.
История возникновения алгоритма пропорционального распределения теряется в глубине веков. В самом примитивном виде, принцип пропорционального распределения использовался ещё в древних цивилизациях при разделе добычи или земельных участков. Формализация этого принципа и его математическое описание появились значительно позже, вместе с развитием алгебры и математического анализа. В простейшем случае, формула алгоритма пропорционального распределения выглядит следующим образом: RK22; = R * (WK22; / ΣWq88;), где RK22; – доля ресурса, получаемая i-ым получателем, R – общий объем ресурса, WK22; – весовой коэффициент i-ого получателя, а ΣWq88; – сумма весовых коэффициентов всех получателей.
Усложненный вариант, включающий поправочный коэффициент, вносит модификацию в эту формулу. Теперь она может выглядеть так: RK22; = R * (WK22; * KK22; / Σ(Wq88; * Kq88;)), где KK22; – поправочный коэффициент для i-ого получателя. Этот коэффициент может принимать значения больше или меньше единицы, в зависимости от того, нужно увеличить или уменьшить долю i-ого получателя по сравнению с базовым пропорциональным распределением. Выбор значения поправочного коэффициента определяется конкретной ситуацией и зависит от факторов, которые необходимо учесть при распределении ресурсов. Определение этих факторов и правильный выбор коэффициентов – это ключевой момент в успешном применении алгоритма.
Применение усложненного алгоритма пропорционального распределения
Применение усложненного алгоритма пропорционального распределения невероятно широко. В экономике он используется при распределении государственного бюджета, инвестиционных ресурсов, финансовых потоков между регионами или отраслями. В бизнесе он находит применение в управлении проектами, планировании бюджета компании, распределении маркетинговых ресурсов и во многих других областях. В логистике алгоритм может быть использован для оптимизации маршрутов доставки, распределения грузов между транспортными средствами, учитывая, например, приоритет доставки и расстояние. Даже в повседневной жизни мы постоянно сталкиваемся с принципами пропорционального распределения – например, при распределении семейного бюджета или времени между различными делами.
Важно понимать, что эффективность алгоритма во многом зависит от правильного выбора весовых коэффициентов и поправочных коэффициентов. Эти коэффициенты должны отражать реальные приоритеты и значимость различных факторов. тельности системы. Поэтому, процесс определения коэффициентов должен быть тщательно продуман и обоснован.
На практике, алгоритм может применяться итеративно. После первого распределения ресурсов, можно проанализировать результаты и скорректировать поправочные коэффициенты, чтобы достичь более оптимального распределения. Этот итеративный подход позволяет постепенно улучшать результаты распределения и приближаться к идеальному варианту. Однако, итеративный процесс может быть трудоемким и требовать значительных временных затрат. Важно установить критерий остановки итераций, чтобы не зацикливаться на постоянном уточнении результатов. Ключ к успеху – в балансе между точностью распределения и затратами на его достижение.
Один из примеров практического применения алгоритма – распределение бюджета маркетинговых кампаний компании. Допустим, компания планирует запустить несколько рекламных кампаний в различных каналах – онлайн-реклама, реклама в социальных сетях, печатная реклама. Весовые коэффициенты могут быть определены на основе анализа эффективности каждого канала в предыдущих кампаниях. Однако, поправочные коэффициенты могут быть добавлены, учитывая, например, срочность достижения определенных целей, конкуренцию в конкретном канале или наличие ограниченных рекламных площадей. В результате, алгоритм позволит оптимально распределить бюджет между различными рекламными каналами, максимизируя отдачу от инвестиций.
С кем конкурирует Алгоритм пропорционального распределения с поправочным коэффициентом
Алгоритм пропорционального распределения с поправочным коэффициентом конкурирует с другими методами распределения ресурсов, каждый из которых имеет свои преимущества и недостатки. Один из таких методов – метод приоритетного распределения. В этом методе, ресурсы распределяются в соответствии с заранее установленными приоритетами получателей. Этот метод прост в применении, но он может быть негибким и не учитывать количественные показатели. В отличие от приоритетного метода, пропорциональный алгоритм учитывает количественные характеристики, но он может быть менее эффективен, если не все важные факторы учтены в весовых коэффициентах.
Другой конкурентный метод – линейное программирование. Этот метод позволяет найти оптимальное распределение ресурсов, учитывая множество ограничений и целей. Однако, линейное программирование является более сложным методом, требующим специальных знаний и программных средств. Алгоритм пропорционального распределения значительно проще в применении, но он может не давать оптимального решения в сложных ситуациях с большим количеством ограни ресурсов между этими получателями. Такой комбинированный подход позволяет объединить преимущества разных методов и получить более эффективный результат. Однако, необходимо помнить, что комбинирование методов может усложнить алгоритм и потребовать значительных временных затрат на его настройку и применение. Ключевым фактором остается анализ и понимание реальной ситуации, а также выбор наиболее подходящего инструмента.
Среди преимуществ усложненного алгоритма пропорционального распределения следует выделить его относительную простоту и понятность. Формулировка алгоритма достаточно интуитивно ясна и не требует специальных математических знаний. Это делает алгоритм доступным для широкого круга пользователей, не имеющих глубокой подготовки в области математического моделирования. Кроме того, алгоритм легко реализуется программно, что позволяет автоматизировать процесс распределения ресурсов и сократить время на его выполнение. Это особенно важно в ситуациях, когда требуется частое перераспределение ресурсов или когда объем данных велик.
Гибкость алгоритма – еще одно важное преимущество. Введение поправочных коэффициентов позволяет учитывать различные факторы, не учтенные в базовых весовых коэффициентах. Это делает алгоритм адаптируемым к разнообразным ситуациям и позволяет более точно распределять ресурсы в соответствии с конкретными условиями. Однако, необходимо отметить, что чрезмерное количество поправочных коэффициентов может усложнить алгоритм и снизить его эффективность. Поэтому, важно выбирать только те факторы, которые действительно существенно влияют на распределение ресурсов.
Конечно, у алгоритма есть и недостатки. Главный недостаток заключается в том, что он не всегда гарантирует оптимальное решение. В сложных ситуациях с большим количеством ограничений и целей, алгоритм может дать лишь приблизительное решение. Более того, точность решения во многом зависит от правильного выбора весовых и поправочных коэффициентов. Неправильный выбор коэффициентов может привести к неэффективному распределению ресурсов и снижению общей эффективности. Поэтому, при использовании алгоритма необходимо проводить тщательный анализ ситуации и обосновывать выбор коэффициентов.
Актуальность алгоритма пропорционального распределения с поправочным коэффициентом для применения в "1С:Предприятие" остается высокой. Этот алгоритм может быть легко интегрирован в существующие информационные системы и использоваться для автоматизации различных процессов распределения ресурсов. Возможности "1С:Предприятия" позволяют создавать гибкие и настраиваемые алгоритмы, учитывающие различные факторы и ограничения. Кроме того, "1С:Предприятие" предоставляет широкие возможности для визуализации результатов распределения ресурсов, что позволяет пользователям легко анализировать и корректировать результаты.
Однако, при применении алгоритма в "1С:Предприятие" необходимо учитывать ограничения системы и выбирать наиболее эффективные методы реализации. В сложных ситуациях с большим количеством ограничений, можно использовать внешние компоненты, интегрированные с "1С:Предприятие", для решения задач линейного или целочисленного программирования. Также, для реализации эвристических методов, таких как генетические алгоритмы, может потребоваться разработка специализированных модулей на встроенном языке "1С:Предприятия".
В целом, алгоритм пропорционального распределения с поправочным коэффициентом — это мощный инструмент для оптимизации различных процессов распределения ресурсов. Его простота и гибкость делают его доступным и эффективным для решения широкого круга задач. Однако, необходимо помнить о его ограничениях и проводить тщательный анализ ситуации, чтобы выбрать наилучшие весовые и поправочные коэффициенты и, при необходимости, использовать более сложные методы для решения сложных задач оптимизации. Правильное использование этого алгоритма в рамках системы «1С:Предприятие» может значительно повысить эффективность работы предприятия и улучшить управление его ресурсами. Постоянное совершенствование алгоритма, учёт новых факторов и интеграция с другими методами оптимизации - это ключевые аспекты успешной реализации алгоритма на практике и достижения максимальной отдачи от его использования.
Применим алгоритм в 1с. Разъяснение начальных данных и полученного результата на примере
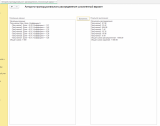
Имеем начальные данные (скриншот с подписью "пример"):
Начальные данные:
Получатели (Имя, Доля, Коэффициент):
- Получатель1: Доля = 0,40, Коэффициент = 0,51
- Получатель2: Доля = 0,13, Коэффициент = 1,29
- Получатель3: Доля = 0,27, Коэффициент = 1,40
- Получатель4: Доля = 0,11, Коэффициент = 1,41
- Получатель5: Доля = 0,01, Коэффициент = 1,08
- Получатель6: Доля = 0,02, Коэффициент = 1,12
- Получатель7: Доля = 0,02, Коэффициент = 1,21
- Получатель8: Доля = 0,03, Коэффициент = 0,66
- Получатель9: Доля = 0,01, Коэффициент = 1,36
Общая сумма: 1 001
Алгоритм Пропорционального распределения, усложненный вариантом, включающим поправочный коэффициент, представляет собой метод распределения некоторого общего ресурса (в данном случае, суммы в 1001 единицу) между несколькими получателями с учетом двух факторов: базовой доли каждого получателя и индивидуального поправочного коэффициента. Базовая доля отражает начальное, заданное распределение ресурса, а коэффициент – корректировку этой доли, учитывающую специфические обстоятельства или приоритеты каждого получателя.
Представьте, что вы делите пирог. Изначально, вы решили, что каждый получит свою долю по определенному размеру. Это и есть "Доля" в нашем алгоритме. Но, возможно, кто-то из гостей – очень важный человек, и вы захотите дать ему немного больше, чем предусмотрено его базовой долей. Или, наоборот, кому-то можно дать немного меньше, если у него уже достаточно. Вот для этого и служит "Коэффициент". Он умножается на базовую долю, изменяя ее размер в большую или меньшую сторону.
Результат выполнения алгоритма над начальными данными (см. скриншот с подписью "пример"):
Результаты распределения:
Получатель1: 205,11
Получатель2: 168,61
Получатель3: 380,05
Получатель4: 155,94
Получатель5: 10,86
Получатель6: 22,52
Получатель7: 24,33
Получатель8: 19,91
Получатель9: 13,67
Общая сумма распределенная: 1 001,00
Общая сумма заданная: 1 001,00
В нашем примере, "Получатель1" имеет долю 0.40, что означает, что изначально ему полагалось 40% от общей суммы, или 400.40 единиц. Однако, его коэффициент равен 0.51, что означает уменьшение его доли. В результате, после применения коэффициента, он получает 205.11 единиц. Обратите внимание, что сумма не просто делится пропорционально, а корректируется индивидуальными коэффициентами каждого получателя. Это ключевое отличие от простого пропорционального распределения.
Вспомним "Получателя2". Его доля — 0.13, что составляет 130.13 единиц изначально. Но коэффициент 1.29 увеличивает его долю. В результате, он получает 168.61 единиц, больше, чем ему изначально полагалось. Можно заметить, что получатели с большими коэффициентами получают больше, чем те, у кого коэффициенты меньше единицы.
Понимание принципа работы алгоритма позволяет не только рассчитать конечное распределение, но и предвидеть изменения в нем при изменении начальных параметров. Например, увеличение коэффициента для "Получателя3" приведет к увеличению его доли в общей сумме, и, соответственно, к уменьшению долей других получателей.
Данный алгоритм подходит для ситуаций, когда необходимо разделить ресурс не только пропорционально, но и с учетом дополнительных факторов, которые могут влиять на справедливость или целесообразность распределения. Это может быть, например, приоритетность заказов на производстве, степень срочности выполнения работ, или иные важные параметры, которые нужно учесть при планировании.
Важно понимать, что сумма распределенного ресурса всегда будет равна заданной общей сумме (в нашем случае 1001). Это свойство алгоритма гарантирует точность распределения и предотвращает ошибки. В то же время, результат распределения сильно зависит от значений базовых долей и поправочных коэффициентов. Различные наборы этих параметров могут привести к существенно различным результатам.
Алгоритм Пропорционального распределения с поправочным коэффициентом обладает большей гибкостью по сравнению с простым пропорциональным распределением. Простое пропорциональное распределение, как следует из названия, делит ресурс строго пропорционально заданным долям. В нем не учитываются никакие дополнительные факторы. Это простой и понятный метод, но он менее адаптивен к изменениям условий.
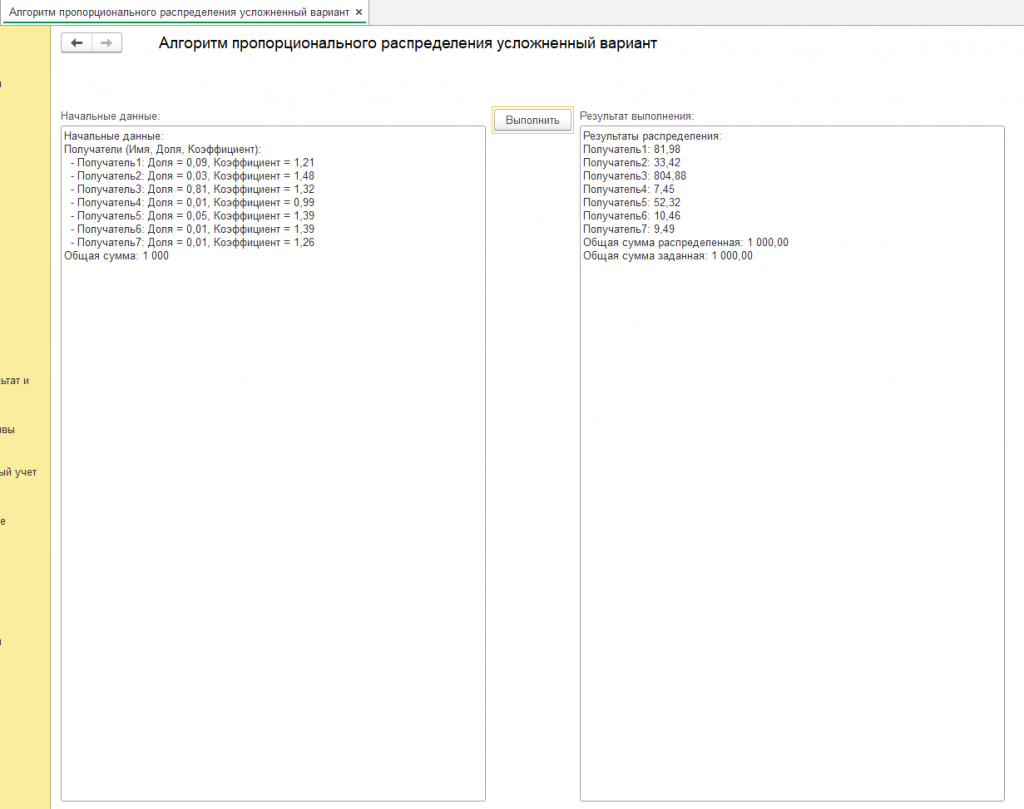
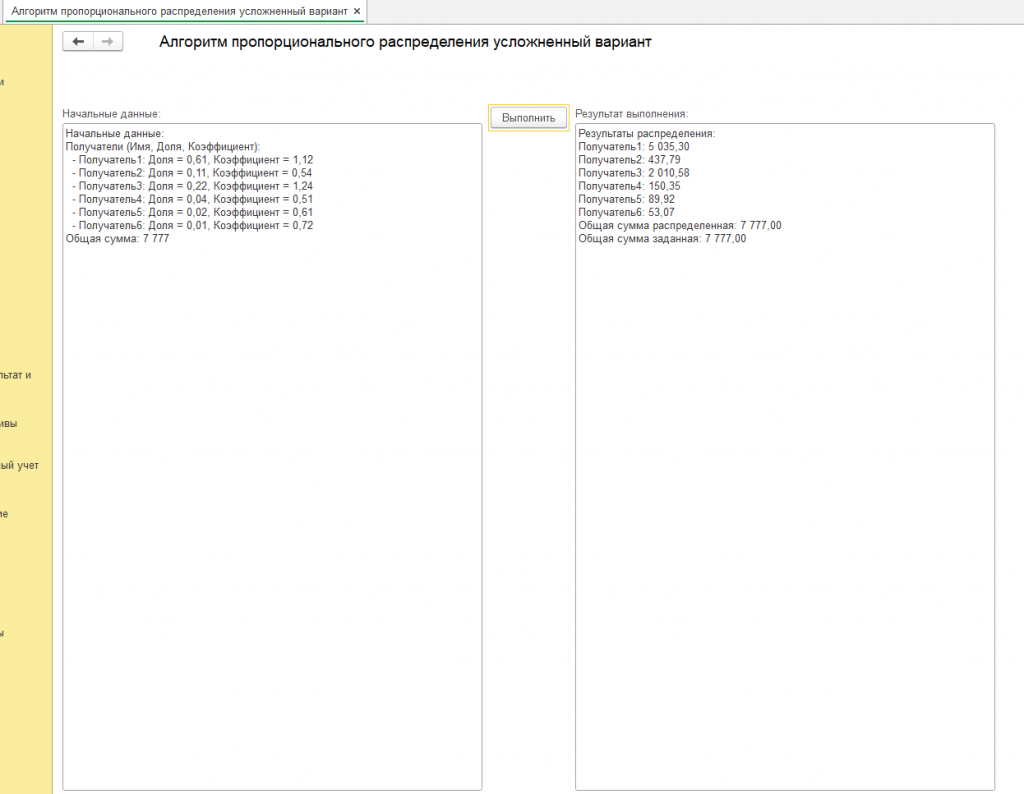
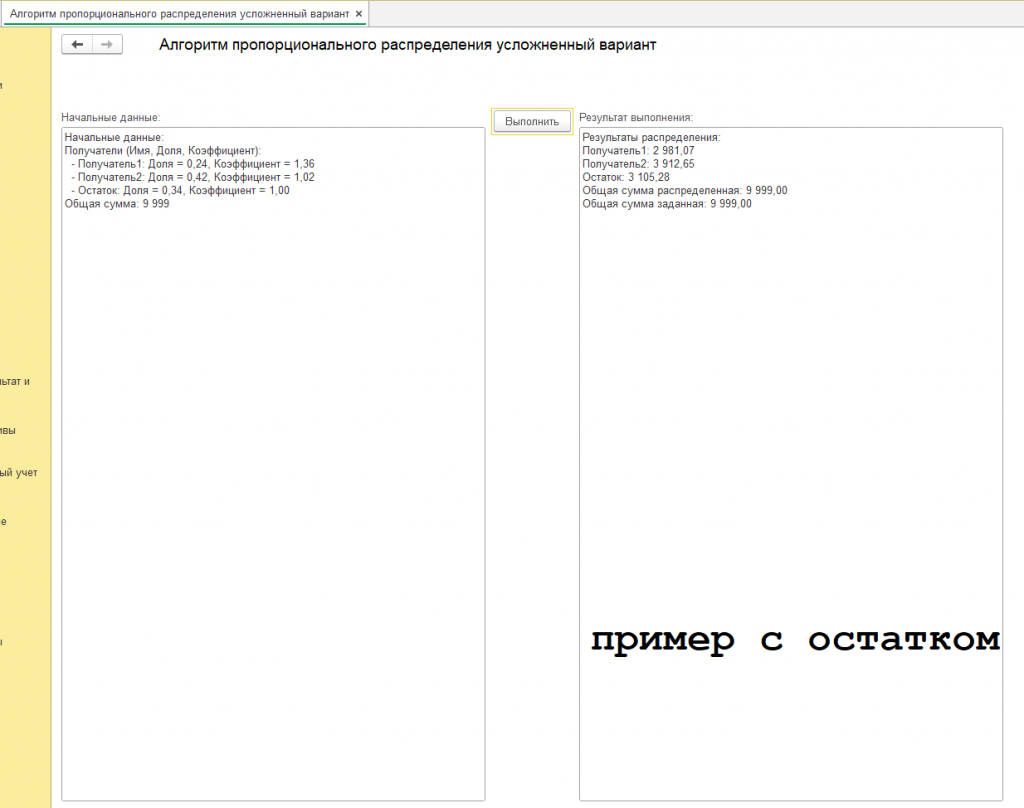
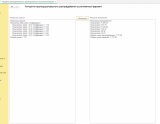
Другие результаты и с другими суммами смотрите на скриншотах.
Обработка должна работать на всех 1с 8.3 на управляемых формах.
В противоположность этому, усложненный вариант с поправочными коэффициентами позволяет учесть множество нюансов, что делает его более точным и справедливым в сложных ситуациях. Однако, этот подход требует более тщательного определения коэффициентов, поскольку некорректные значения могут привести к нежелательным результатам.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.13.82
Вступайте в нашу телеграмм-группу Инфостарт