Алгоритм распределения по приоритету

Определение и фундаментальные принципы Алгоритма распределения по приоритету

         Алгоритм распределения по приоритету – это метод планирования и управления ресурсами, который устанавливает порядок выполнения задач или обработки запросов на основе заранее определённых критериев приоритета. В его основе лежит принцип ранжирования, где каждой задаче присваивается определённая степень важности, влияющая на её позицию в очереди выполнения. Этот алгоритм широко применяется в различных областях, начиная от операционных систем компьютеров и заканчивая сложными системами управления производством. Его суть заключается в эффективном распределении ограниченных ресурсов (время процессора, память, производственные мощности и т.д.) между конкурирующими задачами, отдавая приоритет тем, которые наиболее важны или срочны. Существуют различные способы определения приоритетов, которые зависят от специфики решаемой задачи. Это могут быть временные ограничения, важность задачи для бизнеса, её сложность, ресурсоёмкость и многие другие факторы.

         Эффективность алгоритма распределения по приоритету напрямую зависит от правильного выбора и настройки критериев приоритета. Неправильно подобранные критерии могут привести к ситуациям, когда важные задачи задерживаются, а менее важные выполняются в первую очередь. Это может существенно снизить общую производительность системы или привести к нежелательным последствиям. Поэтому очень важен тщательный анализ и моделирование системы, чтобы точно определить, какие факторы наиболее сильно влияют на её эффективность. В некоторых случаях может потребоваться экспериментировать с различными наборами критериев, чтобы найти оптимальное решение.

         Один из наиболее распространённых подходов к определению приоритетов – использование числовых оценок. Каждой задаче присваивается числовое значение, которое отражает её приоритет. Чем выше значение, тем выше приоритет задачи. Однако, числовые оценки не всегда могут точно отразить сложность и взаимозависимость задач. В более сложных случаях может потребоваться использовать более гибкие и комплексные методы, такие как весовые коэффициенты, которые позволяют учитывать влияние нескольких факторов одновременно. В этом случае, каждая задача получает результирующий приоритет, который является взвешенной суммой оценок по различным критериям. Например, приоритет может зависеть от срока сдачи, стоимости ошибки, сложности задачи и других факторов, каждому из которых может быть присвоен свой весовой коэффициент, отражающий его относительную важность.

         Важно понимать, что алгоритм распределения по приоритету – это не панацея от всех проблем планирования. Он эффективен только в тех случаях, когда критерии приоритета определены корректно и корректно отражают реальные потребности системы. Кроме того, алгоритм должен быть достаточно гибким, чтобы адаптироваться к изменениям в системе. Например, если в систему добавляются новые задачи или меняются приоритеты уже существующих задач, алгоритм должен уметь перестраиваться и сохранять свою эффективность. В таких динамических средах, эффективное управление приоритетами может стать сложной задачей, требующей применения sophisticated методов, которые учитывают взаимосвязи между задачами и изменяющиеся условия.

         Выбор конкретного алгоритма распределения по приоритету зависит от множества факторов, включая размер задачи, ограничения ресурсов, требования к времени отклика, необходимость учитывать внешние факторы и другие параметры. Существуют различные варианты алгоритмов, такие как алгоритм с приоритетной очередью FIFO (First-In, First-Out), алгоритм с приоритетной очередью LIFO (Last-In, First-Out), алгоритм с приоритетами на основе оценок, алгоритмы с динамическим изменением приоритетов и другие. Каждый из этих алгоритмов имеет свои преимущества и недостатки, и выбор подходящего варианта зависит от конкретных условий. В некоторых случаях может потребоваться отклика и избежать нежелательных последствий. В последующих частях мы рассмотрим историю его возникновения, применение в различных областях, сравнение с другими методами, а также выявим его преимущества и недостатки.

Историческое развитие и математическое моделирование Алгоритма распределения по приоритету

         История развития алгоритмов распределения по приоритету тесно связана с развитием вычислительной техники и операционных систем. Первые простые алгоритмы планирования, основанные на принципах FIFO (First-In, First-Out) и LIFO (Last-In, First-Out), появились ещё в ранних операционных системах. Однако, эти алгоритмы были неэффективными для обработки задач с различными требованиями к ресурсам и сроками выполнения. По мере усложнения вычислительных систем и увеличения числа конкурирующих задач, возникла необходимость в более sophisticated алгоритмах планирования, которые учитывали бы приоритеты задач.

         Развитие математической теории планирования и управления дало толчок к созданию более сложных алгоритмов, которые строятся на основе таких математических моделей, как теория очередей, теория графов и линейное программирование. Теория очередей позволяет анализировать и моделировать поведение систем с очередями, определяя вероятности ожидания, среднее время ожидания и другие важные характеристики. Теория графов применяется для представления задач и их зависимостей в виде графов, что позволяет оптимизировать последовательность выполнения задач с учетом их взаимосвязей. Линейное программирование, наконец, позволяет находить оптимальные решения задач распределения ресурсов путем решения систем линейных уравнений и неравенств, что особенно актуально при ограниченных ресурсах.

         Ранние работы в области алгоритмов распределения по приоритету основывались на простых эвристических правилах, которые выбирали задачи для выполнения на основе их приоритета. Однако, эти правила не всегда давали оптимальные результаты, особенно в сложных системах с множеством взаимозависимых задач. Позднее, с развитием математического аппарата, стали появляться алгоритмы, основанные на более строгих математических моделях. Это позволило более точно прогнозировать поведение системы и находить оптимальные решения задачи распределения ресурсов.

         Одним из важных этапов в развитии алгоритмов распределения по приоритету было появление методов динамического планирования. В отличие от статических алгоритмов, которые устанавливают приоритеты задач один раз на весь период работы, динамические алгоритмы позволяют изменять приоритеты задач в зависимости от текущей ситуации. Это особенно важно в динамических средах, где приоритеты задач могут изменяться во время выполнения. ресурсы для решения сложных задач оптимизации. Современные алгоритмы распределения по приоритету используют разнообразные методы оптимизации, такие как генетические алгоритмы, имитационный отжиг и другие метаэвристики. Эти методы позволяют находить приближенные, но достаточно хорошие решения задачи оптимизации за разумное время. Однако, даже с использованием мощных вычислительных ресурсов, нахождение абсолютно оптимального решения задачи распределения ресурсов в сложных системах может быть вычислительно недостижимо. Поэтому, очень важным аспектом является выбор подходящего компромисса между качеством решения и временем его получения.

         Математическое описание алгоритма распределения по приоритету может быть представлено в виде различных моделей, зависящих от конкретных критериев приоритета и ограничений системы. В простейших случаях можно использовать формулы приоритетного ранжирования, например, присваивание весовых коэффициентов каждому критерию и последующее суммирование, либо более сложные математические модели на основе теории графов, линейного программирования или имитационного моделирования.

         В заключение данной части, можно констатировать, что развитие алгоритмов распределения по приоритету тесно связано с прогрессом математических методов оптимизации и вычислительной техники. Современные алгоритмы позволяют решать сложные задачи распределения ресурсов в динамических средах, используя мощный математический аппарат. Однако, выбор конкретного алгоритма и математической модели должен основываться на детальном анализе и моделировании системы.

Применение Алгоритма распределения по приоритету в различных областях

         Алгоритм распределения по приоритету нашел широкое применение в самых разных областях человеческой деятельности. Начиная с фундаментальных компьютерных технологий и заканчивая сложными системами управления производством, ресурсы (время процессора, память) между ними. Для эффективного управления этим процессом используется алгоритм распределения по приоритету, который определяет порядок выполнения задач. Приоритеты могут устанавливаться пользователем, системой или самими приложениями. Например, высокоприоритетные задачи, такие как обработка прерываний или работа системы безопасности, всегда выполняются в первую очередь.

         В сетях связи алгоритм распределения по приоритету используется для управления трафиком. В условиях ограниченной пропускной способности сети, некоторые пакеты данных могут иметь более высокий приоритет, чем другие. Например, пакеты данных, которые передают информацию в режиме реального времени (например, видеоконференция), имеют высокий приоритет, а пакеты данных с низким приоритетом могут быть отложены до тех пор, пока освободятся ресурсы сети.

         В системах управления производством алгоритм распределения по оптимизируя использование производственных мощностей и минимизируя время простоя. В этом случае, приоритезация учитывает не только срочность и важность заказов, но также и технологические ограничения.

         В сфере здравоохранения алгоритм распределения по приоритету применяется в системах управления больницами. В условиях ограниченных ресурсов (врачи, медсестры, аппаратура), некоторые пациенты могут иметь более высокий приоритет, чем другие. Например, пациенты с критическим состоянием всегда получают помощь в первую очередь. В подобных ситуациях, алгоритм распределения по приоритету помогает медицинскому персоналу принимать взвешенные решения и оптимизировать использование ресурсов. Это особенно важно в условиях чрезвычайных ситуаций или при ограниченном финансировании.

         В области аэрокосмической промышленности алгоритм распределения по приоритету играет важнейшую роль в управлении полётами космических аппаратов. В условиях ограниченных ресурсов бортовой системы, некоторые задачи имеют более высокий приоритет, чем другие. Например, задачи обеспечения жизнеобеспечения экипажа и управление ориентацией космического аппарата имеют наивысший приоритет. Алгоритм распределения по приоритету позволяет эффективности, алгоритм определяет приоритетный порядок доставки, минимизируя время доставки и стоимость перевозок. Это помогает предприятиям эффективно управлять своими складскими запасами, оптимизировать использование транспорта и снизить общие затраты на логистику.

         Алгоритм распределения по приоритету - по приоритету, а также обсудим их сильные и слабые стороны.

Сравнение Алгоритма распределения по приоритету с другими методами планирования

         Алгоритм распределения по приоритету – это лишь один из множества методов планирования и управления ресурсами. Его сравнение с другими методами позволяет понять его сильные и слабые стороны и выбрать наиболее подходящий вариант для конкретной задачи.

         Один из наиболее распространенных методов планирования – это метод FIFO (First-In, First-Out). В этом методе задачи выполняются в порядке их поступления, без учета их приоритета. Метод FIFO прост в реализации, но неэффективен в ситуациях, когда некоторые задачи имеют более высокий приоритет, чем другие. В таких случаях важные задачи могут быть заблокированы менее важными, что приводит к снижению общей производительности системы.

         В противовес FIFO существует метод LIFO (Last-In, First-Out), где задачи выполняются в обратном порядке поступления. Этот метод может быть эффективен в ситуациях, когда последние поступившие задачи являются наиболее важными или срочными, но он также может привести к неоправданному затягиванию выполнения ранее поступивших задач, если приоритеты не совпадают с порядком поступления.

         Метод планирования с кратчайшим временем выполнения (Shortest Job First, SJF) выбирает для выполнения задачу с наименьшим временем выполнения. Этот метод минимизирует среднее время ожидания задач, но он может привести к ситуации, когда высокоприоритетные задачи с длительным временем выполнения будут отложены на неопределённый срок.

         Алгоритм планирования Round Robin (круговой опрос) распределяет время процессора между задачами циклически, предоставляя каждому процессу определённый временной квант. Этот алгоритм обеспечивает справедливое распределение ресурсов, но не учитывает приоритеты задач и может быть неэффективным в ситуациях, где некоторые задачи имеют более высокий приоритет. Например, важные задачи могут ожидать выполнения дольше, чем менее важные, из-за равномерного распределения времени.

         В отличие от всех перечисленных методов, алгоритм приоритетного планирования отдает предпочтение задачам с более высоким приоритетом. Однако, без должной реализации, важные задачи могут быть заблокированы менее важными.

         Кроме того, алгоритм распределения по приоритету может конкурировать с более сложными методами оптимизации, такими как линейное программирование, динамическое программирование и методы имитационного моделирования. Эти методы позволяют находить оптимальные решения задач распределения ресурсов, учитывая множество параметров и ограничений.

Преимущества и недостатки Алгоритма распределения по приоритету, актуальность в контексте 1С

         Алгоритм распределения по приоритету, несмотря на свою эффективность, обладает как преимуществами, так и недостатками. Понимание этих аспектов критически важно для принятия обоснованного решения о его применении в конкретной системе.

         К основным преимуществам алгоритма относится возможность приоритетного выполнения важных задач. Это позволяет минимизировать время выполнения критически важных операций, сократить время реакции системы и повысить общую производительность. Благодаря своей гибкости и адаптивности к различным условиям и требованиям, алгоритм может быть эффективно использован в различных системах, от операционных систем до сложных систем управления производством.

         Однако, у алгоритма есть и свои недостатки. Один из самых существенных – это риск "голодания" низкоприоритетных задач. Если высокоприоритетные задачи постоянно поступают в систему, низкоприоритетные задачи могут никогда не быть выполнены. Это может привести к нежелательным последствиям, особенно если низкоприоритетные задачи являются важными, но не являются срочными. Для решения этой проблемы, могут быть использованы различные механизмы, например, ограничение времени выполнения высокоприоритетных задач или периодическая переоценка приоритетов.

         Ещё один недостаток – это сложность определения и настройки критериев приоритета. Неправильно подобранные критерии могут привести к неэффективному распределению ресурсов и снижению производительности системы. Поэтому, перед применением алгоритма необходимо тщательно проанализировать систему и определить наиболее важные критерии приоритета. Процесс настройки критериев может быть сложным и трудоёмким, особенно в больших и сложных системах. Он требует глубокого понимания системы и её требований.

         В контексте платформы "1С:Предприятие", актуальность алгоритма распределения по приоритету достаточно высока. "1С:Предприятие" часто используется для управления сложными бизнес-процессами, где необходимо эффективно распределять ресурсы и выполнять важные задачи в первую очередь. Алгоритм распределения по приоритету может быть использован для оптимизации выполнения фоновых задач, обработки запросов пользователей, управления очередью обработки заказов и других операций.

         Однако, применение алгоритма в "1С:Предприятие" требует дополнительных разработок и настройки. Для реализации алгоритма необходимо разработать соответствующий программный модуль, который будет учитывать специфические требования системы "1С:Предприятие". Кроме того, необходимо тщательно проанализировать систему "1С:Предприятие" и определить наиболее важные критерии приоритета. Неправильно подобранные критерии могут привести к неэффективному распределению ресурсов и снижению производительности системы "1С:Предприятие".

         В заключение, алгоритм приоритизации (или распределения по приоритетам) является мощным и эффективным инструментом управления ресурсами. Однако его применение требует тщательного анализа и корректной настройки параметров. Необходимо опираться на тщательном анализе и моделировании системы, учитывая её специфические требования и ограничения. Только после такого анализа можно принять обоснованное решение о целесообразности применения данного алгоритма.
 

Применение в 1с 8.3, пишем обработку, анализируем результаты

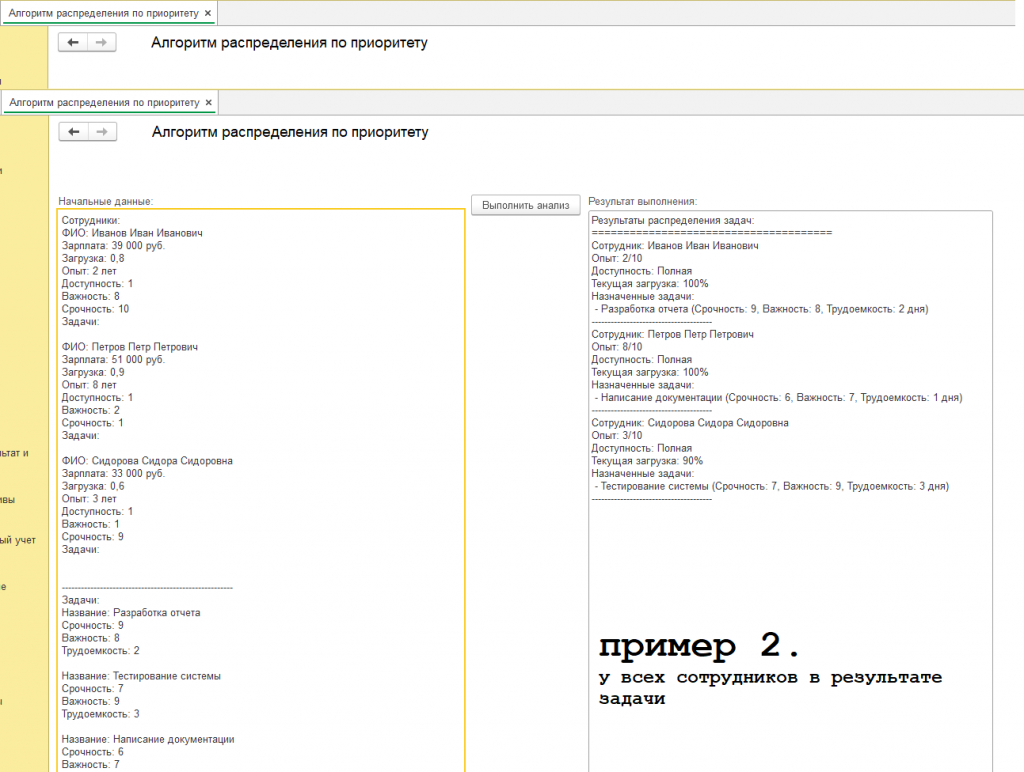
        Представьте себе небольшую компанию, где работают три сотрудника: Иванов Иван Иванович, Петров Петр Петрович и Сидорова Сидора Сидоровна. Каждый из них обладает определенным уровнем опыта работы, получает разную зарплату и имеет разную текущую загрузку проектами. Перед компанией стоит задача распределить три новых проекта между сотрудниками наиболее эффективным способом. Эти проекты – "Разработка отчета", "Тестирование системы" и "Написание документации" – имеют разную степень срочности и важности.

Начальные данные для алгоритма распределения задач по приоритету представляют собой следующую информацию:

Сотрудники:
ФИО: Иванов Иван Иванович
Зарплата: 39 000 руб.
Загрузка: 0,8
Опыт: 2 лет
Доступность: 1
Важность: 8
Срочность: 10
Задачи: 

ФИО: Петров Петр Петрович
Зарплата: 51 000 руб.
Загрузка: 0,9
Опыт: 8 лет
Доступность: 1
Важность: 2
Срочность: 1
Задачи: 

ФИО: Сидорова Сидора Сидоровна
Зарплата: 33 000 руб.
Загрузка: 0,6
Опыт: 3 лет
Доступность: 1
Важность: 1
Срочность: 9
Задачи: 


------------------------------------------------------
Задачи:
Название: Разработка отчета
Срочность: 9
Важность: 8
Трудоемкость: 2

Название: Тестирование системы
Срочность: 7
Важность: 9
Трудоемкость: 3

Название: Написание документации
Срочность: 6
Важность: 7
Трудоемкость: 1

Весовые коэффициенты:
Срочность: 0,5
Важность: 0,3
Опыт: 0,2

1. Сотрудники: Для каждого сотрудника известны следующие параметры: ФИО, зарплата, процент текущей загрузки (от 0 до 1, где 1 – 100% загрузка), количество лет опыта работы, доступность (в данном случае, для всех сотрудников доступность равна 1, что означает полную доступность), оценочная важность сотрудника для компании (от 1 до 10, где 10 – наивысшая важность) и оценочная срочность привлечения сотрудника (от 1 до 10, где 10 – наивысшая срочность).

2. Задачи (проекты): Для каждой задачи известны: название, степень срочности (от 1 до 10, где 10 – наивысшая срочность), степень важности (от 1 до 10, где 10 – наивысшая важность), и трудоемкость в днях.

3. Весовые коэффициенты: Алгоритм использует весовые коэффициенты для определения приоритета задач. Эти коэффициенты показывают, насколько важны срочность, важность и опыт сотрудника при распределении задач. В данном примере срочность имеет вес 0.5, важность – 0.3, а опыт – 0.2. Сумма весов равна 1.

       Алгоритм, используя предоставленные начальные данные и весовые коэффициенты, произвел расчет и предложил следующее распределение:

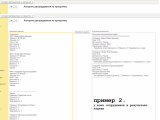
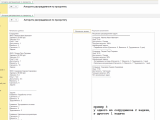
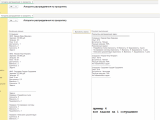
Результаты распределения задач:
======================================
Сотрудник: Иванов Иван Иванович
Опыт: 4/10
Доступность: Частичная
Текущая загрузка: 100%
Назначенные задачи:
 - Разработка отчета (Срочность: 9, Важность: 8, Трудоемкость: 2 дня)
 - Тестирование системы (Срочность: 7, Важность: 9, Трудоемкость: 3 дня)
--------------------------------------
Сотрудник: Петров Петр Петрович
Опыт: 8/10
Доступность: Частичная
Текущая загрузка: 30%
Назначенные задачи:
 - Написание документации (Срочность: 6, Важность: 7, Трудоемкость: 1 дня)
--------------------------------------
Сотрудник: Сидорова Сидора Сидоровна
Опыт: 9/10
Доступность: Частичная
Текущая загрузка: 80%
Нет назначенных задач
--------------------------------------

• Иванов Иван Иванович: Алгоритм назначил Иванову И.И. две задачи: "Разработка отчета" и "Тестирование системы". Хотя у него значительная текущая загрузка (80%), алгоритм посчитал, что его важность для компании и срочность выполнения данных задач перевешивают его загруженность. После выполнения этих задач загрузка Иванова составит 100%, его опыт алгоритм оценил в 4 из 10.

• Петров Петр Петрович: Петрову П.П. назначена одна задача: "Написание документации". Учитывая его высокий опыт и сравнительно низкую текущую загрузку (30%), а также среднюю срочность и важность задачи, алгоритм определил его как наиболее подходящего кандидата для данного проекта. Его опыт оценивается в 8 из 10.

• Сидорова Сидора Сидоровна: Алгоритму не удалось найти подходящую задачу для Сидоровой С.С., несмотря на ее сравнительно высокий уровень опыта и низкую текущую загрузку. Это может быть связано с тем, что срочность и важность задач, которые были доступны, не соответствовали ее профилю или имеющейся у нее загрузке. Её опыт оценивается в 9 из 10.

       Алгоритм стремится найти оптимальное распределение задач, минимизируя риски просрочки и максимизируя эффективность использования ресурсов (в данном случае – времени и опыта сотрудников). Он учитывает как срочность и важность задач, так и загруженность, опыт и важность самих сотрудников. Весовые коэффициенты позволяют настраивать алгоритм под специфические потребности компании. Например, если компания в данный момент ориентирована на быстрое выполнение задач, вес коэффициента срочности можно увеличить.

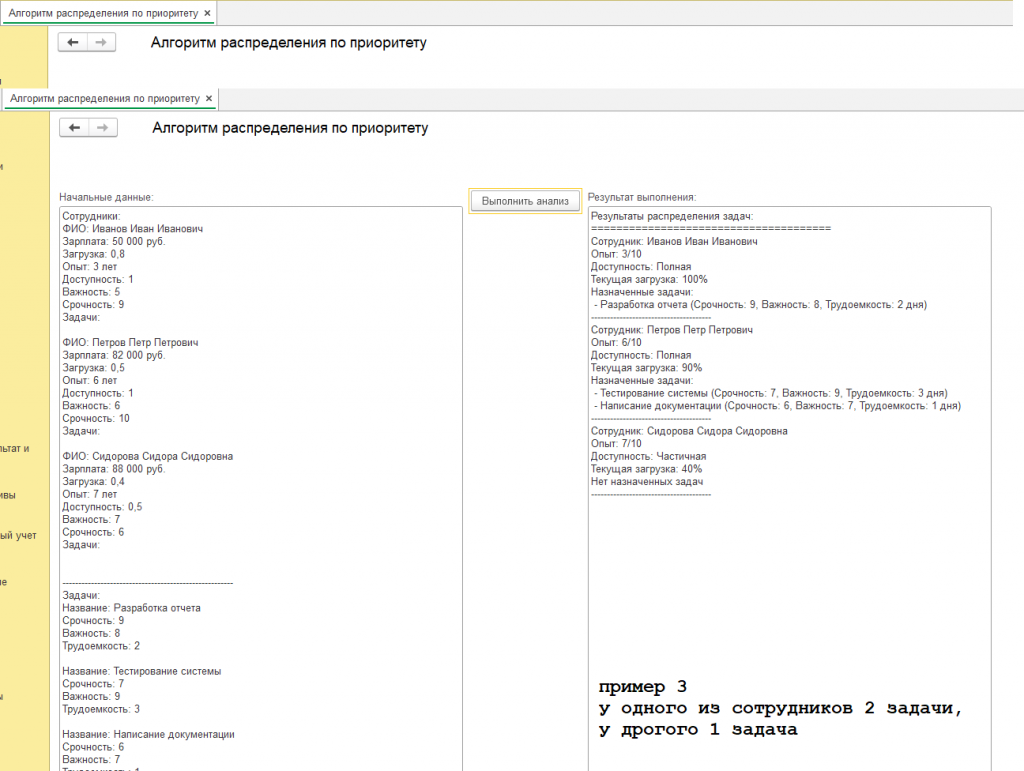
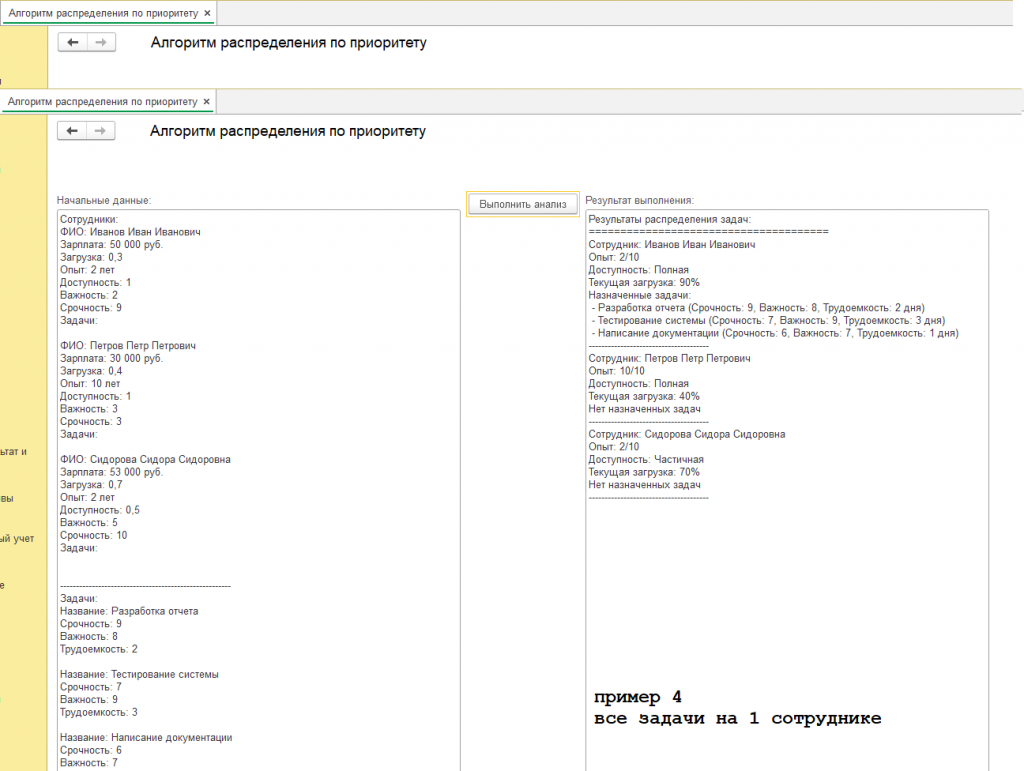
Другие примеры с начальными данными и результатами представлены на скриншотах обработки. Обработка всякий раз формирует новые данные для каждого сотрудника, поэтому вы увидите каждый раз при нажатии на кнопку обработки "Выполнить анализ" новые результаты выполнения алгоритма:

ГСЧ = Новый ГенераторСлучайныхЧисел;
    
    // 1. Сотрудники (массив структур)
    Сотрудники = Новый Массив;
    
    Сотрудник1 = Новый Структура("ФИО,Зарплата,Загрузка,Опыт,Доступность,Важность,Срочность,Задачи");
    Сотрудник1.ФИО = "Иванов Иван Иванович";
    Сотрудник1.Зарплата = ГСЧ.СлучайноеЧисло(30,100)*1000;
    Сотрудник1.Загрузка = Цел(ГСЧ.СлучайноеЧисло(1,9))/10;
    Сотрудник1.Опыт = Цел(ГСЧ.СлучайноеЧисло(1,10));
    Сотрудник1.Доступность = ?(Цел(ГСЧ.СлучайноеЧисло(1,10))<=5,0.5,1);
    Сотрудник1.Важность = Цел(ГСЧ.СлучайноеЧисло(1,10));
    Сотрудник1.Срочность = Цел(ГСЧ.СлучайноеЧисло(1,10));
    Сотрудник1.Задачи = Новый Массив;
    Сотрудники.Добавить(Сотрудник1);

    Сотрудник2 = Новый Структура("ФИО,Зарплата,Загрузка,Опыт,Доступность,Важность,Срочность,Задачи");
    Сотрудник2.ФИО = "Петров Петр Петрович";
    Сотрудник2.Зарплата = ГСЧ.СлучайноеЧисло(30,100)*1000;
    Сотрудник2.Загрузка = Цел(ГСЧ.СлучайноеЧисло(1,9))/10; 
    Сотрудник2.Опыт = ГСЧ.СлучайноеЧисло(1,10);      
    Сотрудник2.Доступность = ?(Цел(ГСЧ.СлучайноеЧисло(1,10))<=5,0.5,1); 
    Сотрудник2.Важность = Цел(ГСЧ.СлучайноеЧисло(1,10));   
    Сотрудник2.Срочность = Цел(ГСЧ.СлучайноеЧисло(1,10));
    Сотрудник2.Задачи = Новый Массив;
    Сотрудники.Добавить(Сотрудник2);

    Сотрудник3 = Новый Структура("ФИО,Зарплата,Загрузка,Опыт,Доступность,Важность,Срочность,Задачи");
    Сотрудник3.ФИО = "Сидорова Сидора Сидоровна";
    Сотрудник3.Зарплата = ГСЧ.СлучайноеЧисло(30,100)*1000;
    Сотрудник3.Загрузка = Цел(ГСЧ.СлучайноеЧисло(1,9))/10;
    Сотрудник3.Опыт = ГСЧ.СлучайноеЧисло(1,10);       
    Сотрудник3.Доступность = ?(Цел(ГСЧ.СлучайноеЧисло(1,10))<=5,0.5,1);
    Сотрудник3.Важность = Цел(ГСЧ.СлучайноеЧисло(1,10));    
    Сотрудник3.Срочность = Цел(ГСЧ.СлучайноеЧисло(1,10));
    Сотрудник3.Задачи = Новый Массив;
    Сотрудники.Добавить(Сотрудник3);

    // 2. Задачи
    ЗадачиВСЕ = Новый Массив;
    
    Задача1 = Новый Структура("Название,Срочность,Важность,Трудоемкость,Приоритет");
    Задача1.Название = "Разработка отчета";
    Задача1.Срочность = 9;
    Задача1.Важность = 8;
    Задача1.Трудоемкость = 2;
    ЗадачиВСЕ.Добавить(Задача1);

    Задача2 = Новый Структура("Название,Срочность,Важность,Трудоемкость,Приоритет");
    Задача2.Название = "Тестирование системы";
    Задача2.Срочность = 7;
    Задача2.Важность = 9;
    Задача2.Трудоемкость = 3;
    ЗадачиВСЕ.Добавить(Задача2);

    Задача3 = Новый Структура("Название,Срочность,Важность,Трудоемкость,Приоритет");
    Задача3.Название = "Написание документации";
    Задача3.Срочность = 6;
    Задача3.Важность = 7;
    Задача3.Трудоемкость = 1;
    ЗадачиВСЕ.Добавить(Задача3);

    // 3. Весовые коэффициенты
    ВесовойКоэффициентСрочности = 0.5;
    ВесовойКоэффициентВажности = 0.3;
    ВесовойКоэффициентОпыта = 0.2;

       В обработке после начальных данных происходят следующие этапы: 1) Расчет приоритета для задач 2) Сортировка задач по приоритету (по убыванию) 3) Сортировка сотрудников по пригодности (опыт * доступность) 4) Распределение задач: Найти наиболее подходящего сотрудника , Проверить загрузку сотрудника 5) Формирование результата.

Возможные усложнения начальных данных и соответствующие результаты:

         Учет зависимостей между задачами: В реальных условиях задачи могут зависеть друг от друга (например, "Разработка отчета" должна быть выполнена перед "Тестированием системы"). Добавление информации о зависимостях в начальные данные значительно усложнит алгоритм, но позволит получить более точное и реалистичное распределение задач. В результате алгоритм должен был бы обеспечить выполнение всех зависимых задач в правильном порядке, даже если это приведет к перераспределению задач между сотрудниками или увеличению сроков выполнения.

         Учет квалификации сотрудников: Вместо общего опыта можно добавить информацию о специализации сотрудников (например, "Разработчик", "Тестировщик", "Технический писатель"). Это позволит алгоритму назначать задачи сотрудникам с соответствующей квалификацией, даже если это означает временное отклонение от строгого приоритета по срочности/важности. Результатом станет более точное соответствие задач квалификации сотрудников.

         Учет стоимости выполнения задач: Включение информации о стоимости часа работы каждого сотрудника позволит алгоритму оптимизировать распределение задач с точки зрения стоимости. Алгоритм может выбрать сотрудника с более низкой оплатой труда, но достаточной квалификацией для выполнения задачи, чтобы снизить общие затраты компании. Результатом стало бы снижение общей стоимости выполнения работ без ущерба для сроков и качества.

         Учет рисков: Можно добавить информацию о вероятности возникновения непредвиденных проблем при выполнении каждой задачи. Это позволит алгоритму учитывать риски и распределять задачи, минимизируя вероятность возникновения задержек. В результате распределение стало бы более устойчивым к неожиданным трудностям.

         Многокритериальная оптимизация: Вместо использования простых весовых коэффициентов можно использовать методы многокритериальной оптимизации. Это позволит алгоритму учитывать несколько целей одновременно (например, минимизацию затрат и соблюдение сроков) и находить компромиссные решения. Результатом было бы распределение, оптимальное по нескольким параметрам.

         Динамическое планирование: Вместо статического распределения задач на основе начальных данных, алгоритм можно адаптировать для динамического планирования, где он будет перераспределять задачи в зависимости от изменений в ситуации (например, задержки в выполнении одной из задач). Это значительно повысит его адаптивность к изменениям. Результатом был бы самонастраивающийся план, реагирующий на изменения в режиме реального времени.

         Включение каждого из этих усложнений в начальные данные приведет к созданию более сложного и точного алгоритма распределения задач, что в конечном итоге приведет к повышению эффективности работы компании и снижению рисков просрочки проектов. Однако, увеличение сложности алгоритма неизбежно повлечет за собой рост вычислительной сложности и времени, необходимого на его работу. Выбор оптимального уровня сложности алгоритма зависит от конкретных условий и потребностей компании.

         В контексте "1С:Предприятие", алгоритм распределения задач по приоритету может быть реализован как самостоятельное приложение.