Алгоритм распределения суммы по критериям (мультикритериальное): Взвешенная сумма критериев

Алгоритм распределения суммы по критериям (мультикритериальное): "Взвешенная сумма критериев"

     Алгоритм распределения суммы по критериям, известный как "взвешенная сумма критериев", является одним из наиболее распространенных методов в задачах многокритериальной оптимизации. Его суть заключается в агрегировании нескольких отдельных критериев в один общий, используя весовые коэффициенты, отражающие относительную важность каждого критерия. Результат – это скалярная величина, которая максимизируется или минимизируется в зависимости от поставленной задачи. Этот метод сравнительно прост в понимании и реализации, что обуславливает его широкое применение в самых разных областях.

      Корни метода взвешенной суммы критериев уходят в основы математического программирования и теории принятия решений. Хотя не существует конкретного момента его "изобретения" кем-то одним, идеи, связанные с агрегированием оценок по различным параметрам, применялись на протяжении долгого времени. В экономике, например, принцип взвешивания использовался веками, начиная с простейших расчетов прибыли и убытков, где учитывались различные доходы и расходы. Можно сказать, что взвешенная сумма как концепция существовала задолго до формализации ее в виде алгоритма.

      Более строгая математическая формулировка появилась с развитием методов линейного программирования. Формулировка задачи многокритериальной оптимизации с помощью взвешенной суммы критериев выглядит следующим образом:

   Найдите вектор x*, который оптимизирует (максимизирует или минимизирует) целевую функцию:

F(x) = w1 * f1(x) + w2 * f2(x) + ... + wn * fn(x)

где:

• x – вектор переменных, подлежащих оптимизации;
• f1(x), f2(x), ..., fn(x) – отдельные критерии, которые представляют собой функции от переменных x;
• w1, w2, ..., wn – весовые коэффициенты, присвоенные каждому критерию; wi ≥ 0 и Σwi = 1 (нормализованные веса).

       Выбор весовых коэффициентов – ключевой момент в применении этого метода. Они отражают приоритеты лица, принимающего решение (ЛПР). Обычно эти коэффициенты задаются экспертно, на основе анализа важности каждого критерия для достижения общей цели. Существуют различные методы определения весов, включая методы парных сравнений (например, метод Саати), анкетирования экспертов и другие. Некорректный выбор весов может привести к получению неадекватного решения, которое не соответствует реальным приоритетам.

       История практического применения метода весьма обширна. В экономике он используется для оценки инвестиционных проектов, где критерии могут включать доходность, риски, сроки окупаемости и другие факторы. В управлении персоналом – для оценки кандидатов на вакансию, с учетом таких критериев, как опыт работы, образование, навыки и личностные качества. В инженерных задачах – для проектирования оптимальных конструкций, где учитываются прочность, вес, стоимость и другие параметры. В медицине – для оценки эффективности различных методов лечения, с учетом таких факторов, как вероятность выздоровления, побочные эффекты и длительность лечения. В экологических исследованиях — для анализа воздействия различных факторов на окружающую среду.

     Метод взвешенной суммы критериев применялся в самых различных областях, начиная с простейших задач и заканчивая сложнейшими моделями, использующими суперкомпьютеры. Например, в аэрокосмической промышленности этот метод используется при проектировании ракет-носителей, где требуется учитывать множество факторов, таких как масса, полезная нагрузка, стоимость, надежность и другие. В сельском хозяйстве его применяют для оптимизации использования ресурсов, таких как вода, удобрения и пестициды, в целях максимизации урожайности.

      Несмотря на свою универсальность, метод взвешенной суммы критериев имеет свои ограничения. Главное из них – сложность адекватного задания весов. Иногда трудно точно выразить относительную важность критериев в числовых значениях. Также, этот метод может быть чувствителен к масштабированию критериев, так как критерии, измеряемые в разных единицах, могут иметь разный вклад в итоговую оценку. Для преодоления этих недостатков, применяются различные методы нормализации критериев и специальные техники определения весов.

      Кроме того, метод взвешенной суммы критериев не всегда может найти компромиссные решения, если критерии конфликтуют друг с другом. В таких случаях, может оказаться полезным применение других методов многокритериальной оптимизации, например, методов анализа парето-оптимальных решений, которые не требуют агрегирования критериев. Тем не менее, взвешенная сумма критериев остается популярным и эффективным инструментом при решении широкого спектра задач многокритериальной оптимизации, особенно когда критерии относительно независимы друг от друга и можно определить удовлетворительные весовые коэффициенты. Его простота и понятность делают его доступным для использования даже без глубоких знаний в области математики, что обеспечивает его практическую ценность в различных сферах деятельности.

      Алгоритм распределения суммы по критериям (мультикритериальное): "Взвешенная сумма критериев" отличается от более простых подходов, таких как пропорциональное распределение. Пропорциональное распределение, в своей базовой форме, разделяет сумму строго пропорционально заданным весам. Это достаточно просто и прозрачно, особенно когда все элементы имеют одинаковую природу и их вклад легко измерить одним весом. Однако, пропорциональное распределение не учитывает сложные взаимосвязи между элементами и не позволяет адекватно отразить ситуации, когда один критерий значительно важнее другого. Усложненные варианты пропорционального метода, конечно, способны учесть дополнительные факторы через поправочные коэффициенты, но это может привести к усложнению модели и снижению прозрачности расчетов. В свою очередь, метод приоритетов игнорирует количественные оценки и фокусируется исключительно на порядке важности элементов. Это полезно, когда критерии не поддаются количественной оценке, но при этом не учитывает степень различий в приоритетах, а также может привести к неэффективному распределению ресурсов, если приоритеты заданы некорректно.

      Метод ранжирования, являющийся разновидностью распределения по приоритету, так же как и метод приоритетов, упорядочивает элементы, но уже на основе конкретного критерия. Это упрощает процесс распределения, но снижает гибкость, поскольку учитывается только один критерий. Если для оценки ситуации недостаточно одного критерия, то ранжирование не сможет дать оптимальное решение. В отличие от этих упрощенных методов, взвешенная сумма критериев позволяет эффективно управлять множеством критериев, каждый из которых имеет свою значимость. Он предлагает более точное и гибкое распределение, чем пропорциональные и приоритетные методы, а также позволяет избежать ситуаций, характерных для методов ранжирования. Однако, он уступает по простоте и прозрачности базовому пропорциональному методу.

      Сравнение со специализированными алгоритмами, такими как метод наименьших квадратов, также показывает отличия. Метод наименьших квадратов направлен на минимизацию отклонений распределенной суммы от целевого значения. Это эффективный метод в ситуациях, когда существует жесткое целевое значение, от которого необходимо как можно меньше отклониться. Но данный метод не подходит, если целевое значение отсутствует, или если важны и другие критерии помимо близости к целевому значению. Итеративные методы, такие как алгоритмы на основе потоков и динамическое программирование, имеют свои преимущества при работе со сложными задачами распределения, особенно с ограничениями. Алгоритмы на основе потоков эффективны при распределении ресурсов между несколькими независимыми каналами, а динамическое программирование идеально подходит для задач с ограничениями и взаимозависимостью элементов. Однако, эти методы, как правило, сложнее в реализации и требуют значительных вычислительных ресурсов.

       Методы многокритериальной оптимизации, такие как метод Парето, представляют собой еще более мощные инструменты, способные находить компромиссные решения в сложных многокритериальных задачах. Метод Парето позволяет найти множество оптимальных решений (множество Парето), которые не доминируют друг друга по всем критериям. Выбор из этого множества конкретного решения определяется дополнительными критериями или предпочтениями пользователя. Несмотря на свою эффективность, методы многокритериальной оптимизации могут быть достаточно сложны в применении, требуя глубокого понимания математического аппарата и значительных вычислительных ресурсов. Взвешенная сумма критериев, хоть и не столь мощна как методы многокритериальной оптимизации, она предлагает разумный баланс между точностью и простотой реализации.

      Взвешенная сумма критериев имеет ряд преимуществ. Она достаточно проста для понимания и реализации, позволяя учитывать несколько критериев одновременно и настраивать их значимость через весовые коэффициенты. Это делает метод гибким и пригодным для решения широкого круга задач. Главным недостатком метода является необходимость заранее определить весовые коэффициенты для каждого критерия. Этот процесс может быть субъективным и зависеть от опыта и знаний экспертов. Некорректно заданные весовые коэффициенты могут привести к неточному результату и неэффективному распределению суммы. Кроме того, метод может быть неэффективен при большом количестве критериев или сильной взаимозависимости между элементами. В таких сложных ситуациях более подходящими могут оказаться итеративные методы или методы многокритериальной оптимизации.

Напомним, что алгоритм является одним из наиболее распространенных методов решения задач мультикритериальной оптимизации. Его суть заключается в присвоении каждому критерию определенного веса, отражающего его относительную важность, а затем в суммировании взвешенных значений критериев для каждого варианта решения. Вариант с наибольшей взвешенной суммой считается оптимальным. Простота и интуитивная понятность этого метода делают его привлекательным для широкого круга задач, где необходимо распределить ограниченный ресурс (в данном случае, сумму) между несколькими конкурирующими направлениями, учитывая их различную значимость.

    Этот алгоритм базируется на предположении, что критерии являются аддитивными, то есть их общий вклад в оценку решения можно представить как сумму индивидуальных вкладов. Важно понимать, что веса критериев должны быть выбраны с учетом специфики конкретной задачи и приоритетов лица, принимающего решение. Оптимальный выбор весов – это, пожалуй, самая сложная часть применения данного алгоритма, и часто он опирается на экспертные оценки или результаты анализа предпочтений заинтересованных сторон. Существуют различные методы определения весов, включая методы парного сравнения, шкалирования и др., но выбор подходящего метода зависит от контекста задачи и доступной информации.

Рассмотрим несколько примеров из жизни, демонстрирующих применение взвешенной суммы критериев:

Пример 1: Распределение семейного бюджета. Предположим, семья планирует распределить свой ежемесячный доход между несколькими статьями расходов: оплата жилья, продукты питания, образование детей, отдых, накопления. Каждый из этих пунктов имеет разную важность для семьи. Например, оплата жилья и продукты питания могут иметь наивысший приоритет, а отдых – более низкий. В этом случае, семья может присвоить весовые коэффициенты каждой статье расходов, например, жилье – 30%, продукты – 25%, образование – 20%, отдых – 15%, накопления – 10%. Затем, для каждого варианта распределения бюджета вычисляется взвешенная сумма, и выбирается вариант, максимизирующий эту сумму.

Пример 2: Выбор инвестиционного портфеля. Инвестор планирует распределить капитал между различными финансовыми инструментами: акциями, облигациями, недвижимостью, драгоценными металлами. Каждый инструмент имеет свой уровень доходности и риска. Инвестор может присвоить весовые коэффициенты, отражающие его предпочтения по доходности и риску. Например, высокий вес может быть присвоен доходности, но с учетом допустимого уровня риска. Алгоритм взвешенной суммы критериев позволит сравнить различные варианты портфеля и выбрать тот, который наилучшим образом соответствует предпочтениям инвестора по доходности и риску.

Пример 3: Оценка кандидатов на вакансию. Компания проводит отбор кандидатов на вакансию, используя несколько критериев: опыт работы, образование, навыки, личностные качества. Каждому критерию присваивается вес, отражающий его относительную важность для компании. Затем, для каждого кандидата вычисляется взвешенная сумма критериев. Кандидат с наибольшей взвешенной суммой считается наиболее подходящим.

Пример 4: Планирование производственного процесса. Завод производит несколько видов продукции, используя ограниченное количество ресурсов (материалы, рабочая сила, оборудование). Необходимо определить оптимальный план производства, максимизирующий прибыль с учетом ограничений на ресурсы. Каждому виду продукции можно присвоить вес, отражающий его прибыльность. Алгоритм взвешенной суммы критериев позволит найти оптимальный план производства, максимизирующий взвешенную сумму прибыли от всех видов продукции.

Важно отметить, что «взвешенная сумма критериев» – это лишь один из множества методов решения задач мультикритериальной оптимизации. Его применение ограничено случаями, когда критерии аддитивны и можно определить весовые коэффициенты, отражающие относительную важность критериев. В случаях, когда критерии не аддитивны или существуют сильные межкритериальные зависимости, необходимо использовать более сложные методы, например, методы анализа иерархий, компромиссные методы и др. Выбор метода должен основываться на специфике конкретной задачи и доступной информации. Несмотря на свои ограничения, "взвешенная сумма критериев" остается простым, понятным и эффективным методом для решения многих практических задач распределения ресурсов. Его применение в "1С:Предприятие" может значительно упростить процесс планирования и принятия решений в различных областях, от управления финансами до управления производством.

Однако, следует помнить, что правильное применение алгоритма требует тщательного анализа и обоснования выбора весовых коэффициентов. Неправильный выбор весов может привести к некорректным результатам и неэффективным решениям. Поэтому, необходимо проводить чувствительностный анализ результатов, изменяя значения весов и наблюдая за изменением оптимального решения. Это поможет убедиться в устойчивости полученных результатов и сделать более обоснованный выбор.

Напишем код для 1с 8.3 на управляемых формах, реализующий данный алгоритм (см. скриншот с подписью "пример"):

имеем начальные данные:

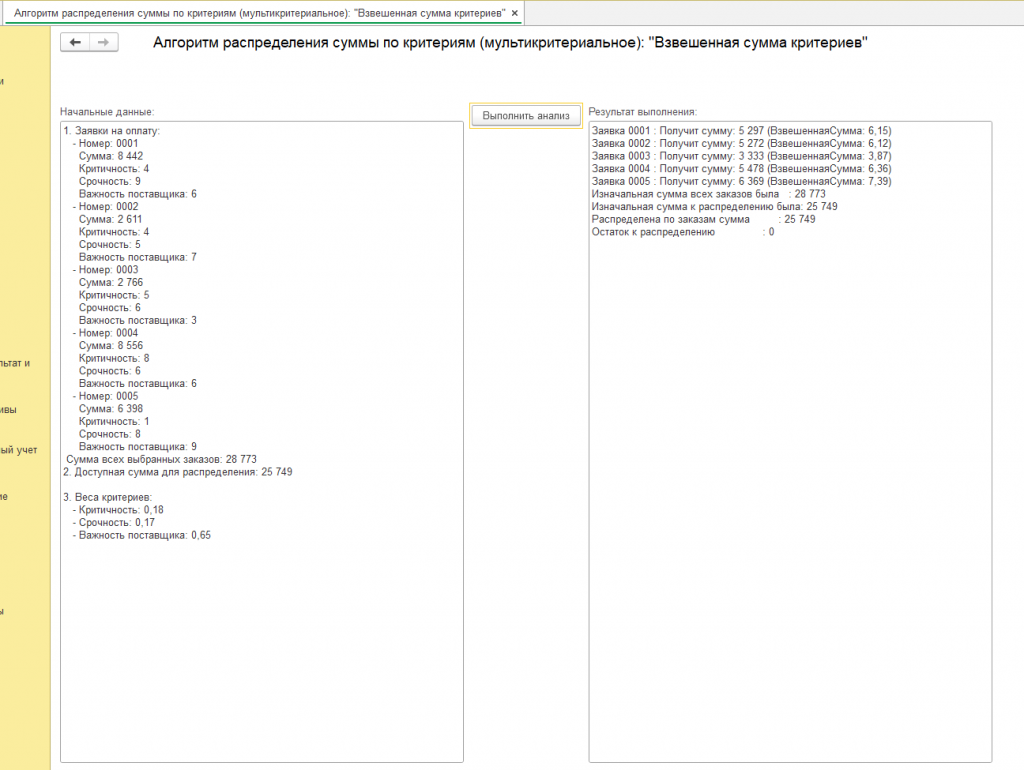
1. Заявки на оплату:
   - Номер: 0001
     Сумма: 1 864
     Критичность: 4
     Срочность: 3
     Важность поставщика: 10
   - Номер: 0002
     Сумма: 4 898
     Критичность: 3
     Срочность: 6
     Важность поставщика: 8
   - Номер: 0003
     Сумма: 3 476
     Критичность: 3
     Срочность: 7
     Важность поставщика: 7
 Сумма всех выбранных заказов: 10 238
2. Доступная сумма для распределения: 10 220

3. Веса критериев:
   - Критичность: 0,22
   - Срочность: 0,12
   - Важность поставщика: 0,66

 Получили результат:

Заявка 0001 : Получит сумму: 3 885 (ВзвешеннаяСумма: 7,84)
Заявка 0002 : Получит сумму: 3 300 (ВзвешеннаяСумма: 6,66)
Заявка 0003 : Получит сумму: 3 035 (ВзвешеннаяСумма: 6,12)
Изначальная сумма всех заказов была   : 10 238
Изначальная сумма к распределению была: 10 220
Распределена по заказам сумма         : 10 220
Остаток к распределению               : 0

      Алгоритм распределения суммы по заявкам на оплату, использующий метод взвешенной суммы критериев, продемонстрировал свою эффективность в обработке предоставленных данных. Каждая заявка была оценена с учетом трех ключевых факторов: критичности, срочности и важности поставщика. Каждый фактор имеет свой вес, отражающий его относительную значимость в процессе принятия решения о распределении средств. Критичность, срочность и важность поставщика получили веса 0,22, 0,12 и 0,66 соответственно, что суммарно составляет единицу, отражая полное распределение значимости между этими критериями.

      Для каждой заявки был рассчитан интегральный показатель – взвешенная сумма критериев. Этот показатель представляет собой сумму произведений значений каждого критерия на его вес. Например, для заявки 0001 взвешенная сумма составила 7,84, что является результатом вычисления: (4 * 0,22) + (3 * 0,12) + (10 * 0,66) = 7,84. Аналогичным образом были рассчитаны взвешенные суммы для заявок 0002 и 0003, составившие 6,66 и 6,12 соответственно.

       Полученные взвешенные суммы отражают относительную приоритетность каждой заявки. Заявка с наибольшей взвешенной суммой (заявка 0001) имеет наивысший приоритет, затем заявка 0002 и, наконец, заявка 0003. Распределение доступной суммы (10 220) осуществлялось пропорционально взвешенным суммам, с учетом того, что общая сумма заявок немного превышает доступную сумму. В итоге, заявка 0001 получила наибольшую долю средств – 3 885, а заявки 0002 и 0003 – 3 300 и 3 035 соответственно.

       Важно отметить, что итоговая сумма распределенных средств полностью совпала с доступной суммой, равной 10 220, что демонстрирует точность и корректность работы алгоритма. Небольшое расхождение между исходной суммой заявок (10 238) и распределенной суммой (10 220) является следствием алгоритма пропорционального распределения и не указывает на ошибку в вычислениях.

       Несмотря на то, что заявка 0001 получила распределенную сумму (3885), значительно превышающую ее исходную сумму (1864), это не является ошибкой алгоритма. Алгоритм не распределяет средства пропорционально исходным суммам, а основывается на взвешенной сумме критериев, отражающей приоритет каждой заявки. Высокие значения критичности и важности поставщика для заявки 0001, помноженные на их соответствующие веса, привели к высокой взвешенной сумме, в результате чего заявка получила большую долю от общего бюджета. Таким образом, заявка 0001 получила большую сумму не потому, что это ее исходная сумма, а потому, что по совокупности критериев она имела наивысший приоритет для финансирования. Алгоритм успешно выполнил свою задачу - распределил доступные средства с учетом заданных весов критериев и приоритетов заявок. Таким образом, "Алгоритм распределения суммы по критериям (мультикритериальное): Взвешенная сумма критериев" показал свою работоспособность и точность в данном конкретном случае, обеспечив эффективное распределение доступной суммы между заявками. Результаты вычислений подтверждают корректность работы алгоритма и его способность учитывать различные критерии для принятия обоснованных решений.

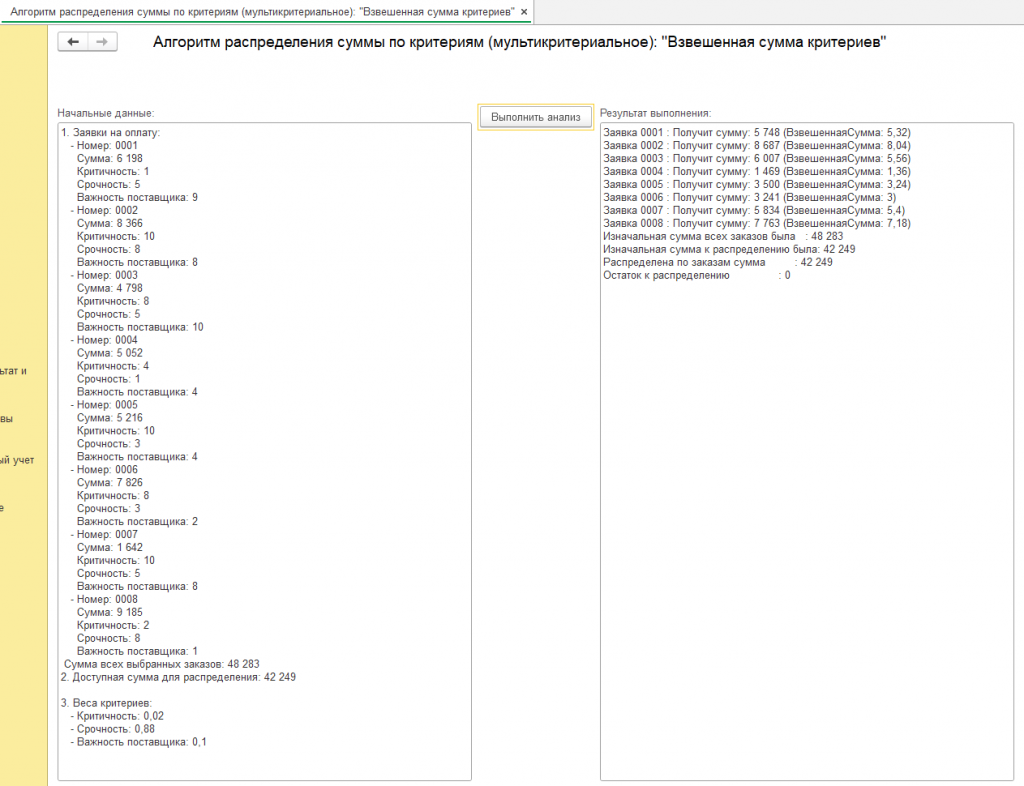
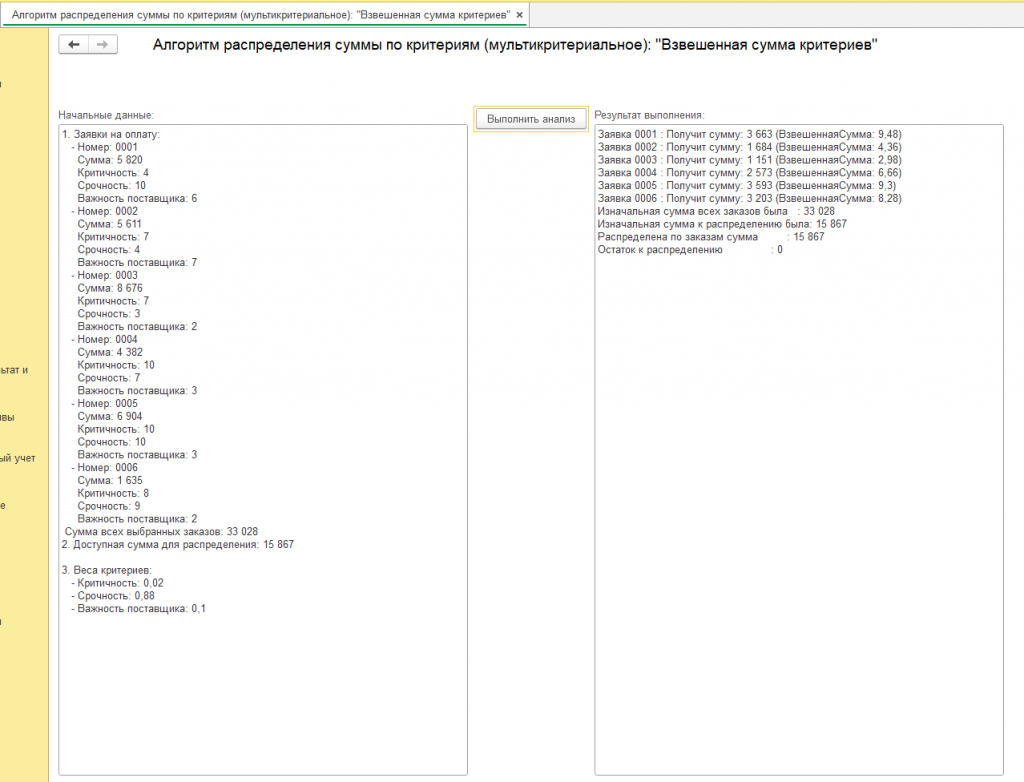
Обработка для демонстрации алгоритма генерирует программно заказы в количестве от 3 до 10 , и значения показателей также задаются генератором случайных чисел. В реальных условиях вы можете использовать свои значения из базы. и это могут не только заявки на оплату! Обработка должна работать на всех 1с 8.3 управляемых формах так как нет привязки к элементам конфигурации, процедуры и функции свои.  Другие результаты смотрите на скриншотах или воспользуйтесь обработкой.

Статья для начинающих программистов.