Мультикритериальное распределение представляет собой подход к принятию решений, при котором выбор оптимального варианта осуществляется на основе анализа нескольких, зачастую противоречивых, критериев. В отличие от однокритериальных задач, где решение сводится к максимизации или минимизации единственного показателя, мультикритериальность требует балансировки между различными целями. Например, при планировании производства может возникнуть необходимость одновременно сократить сроки выполнения заказов, минимизировать затраты и обеспечить высокое качество продукции. Такие задачи характерны для экономики, логистики, управления проектами и других областей, где решения влияют на множество аспектов деятельности. Основная сложность здесь заключается в том, что улучшение одного критерия часто приводит к ухудшению другого, что требует поиска компромиссов. Для работы с такими сценариями разработаны методы, позволяющие систематизировать и ранжировать альтернативы, среди которых особое место занимает метод Парето.
Метод Парето, названный в честь итальянского экономиста Вильфредо Парето, основан на принципе оптимальности, согласно которому решение считается эффективным, если невозможно улучшить один критерий без ухудшения другого. Это понятие тесно связано с концепцией «Парето-фронта» — множества решений, каждое из которых не доминируется другими. Например, если рассматривать два критерия — стоимость и время выполнения заказа, Парето-оптимальными будут те варианты, где нельзя сократить сроки без увеличения затрат или снизить затраты без продления сроков. Метод Парето не предполагает единственного «лучшего» решения, а выделяет набор эффективных альтернатив, из которых выбор осуществляется с учётом дополнительных предпочтений или ограничений. Этот подход особенно полезен в ситуациях, где субъективные приоритеты заказчика или внешние условия могут влиять на окончательное решение. Однако для практического применения метода требуются инструменты, позволяющие визуализировать и анализировать Парето-фронт, что часто связано с использованием специализированного программного обеспечения или математических моделей.
В рамках методологии Парето выделяют различные подходы к обработке многокритериальных задач, такие как метод эффективности и метод приоритетов. Метод эффективности фокусируется на оценке того, насколько каждая альтернатива соответствует заданным критериям в целом. Здесь ключевым понятием является «эффективность по Парето», которая подразумевает, что решение не может быть улучшено по одному параметру без ухудшения других. Например, при выборе поставщика анализируются стоимость, качество сырья и сроки поставки. Если ни один из поставщиков не превосходит другого по всем трём параметрам одновременно, все они считаются Парето-эффективными. Этот метод полезен на этапе предварительного отбора, когда необходимо сузить круг вариантов до тех, которые заведомо не уступают другим. Однако он не даёт ответа на вопрос, какое из эффективных решений предпочесть, что требует применения дополнительных методов.
Метод приоритетов, в отличие от метода эффективности, предполагает ранжирование критериев по степени важности. Например, если в проекте критически важен срок сдачи, а бюджет и качество являются второстепенными факторами, решения будут оцениваться в первую очередь по временным показателям. Этот подход позволяет упростить задачу, сводя её к последовательной оптимизации: сначала выбираются варианты, оптимальные по главному критерию, затем среди них отбираются те, что лучше соответствуют второму по значимости критерию, и так далее. Такой метод эффективен в условиях, когда существует чёткая иерархия целей, но он может привести к субоптимальным решениям, если второстепенные критерии оказывают существенное влияние на результат. Например, сосредоточившись на минимизации затрат, можно выбрать поставщика с низкой ценой, но ненадёжными сроками поставки, что в итоге приведёт к срыву проекта. Поэтому метод приоритетов требует тщательного анализа взаимосвязей между критериями.
Различия между методом эффективности и методом приоритетов заключаются в их подходе к обработке многокритериальности. Первый акцентирует внимание на поиске всех возможных компромиссов, не выделяя «главных» и «второстепенных» параметров, что делает его универсальным, но трудоёмким. Второй упрощает задачу за счёт иерархии критериев, но рискует упустить из виду альтернативы, которые балансируют между параметрами более гибко. Выбор между ними зависит от конкретной ситуации: если приоритеты чётко определены и неизменны, метод приоритетов позволяет быстро принять решение. Если же важно рассмотреть все возможные варианты и проанализировать компромиссы, метод эффективности предоставляет более полную картину. На практике эти подходы часто комбинируют — например, сначала отбирают Парето-эффективные решения, а затем применяют метод приоритетов для окончательного выбора.
Актуальность методов Парето в современных условиях обусловлена ростом сложности управленческих задач и необходимостью учитывать множество факторов при принятии решений. В эпоху цифровизации и big data анализ многокритериальных задач становится более доступным благодаря алгоритмам машинного обучения и инструментам визуализации. Однако ключевой вызов заключается в том, чтобы адаптировать классические методы, такие как Парето-оптимизация, к динамически меняющимся условиям. Например, в логистике необходимо оперативно пересматривать планы поставок при изменении спроса или сбоях в цепочках. Здесь методы, основанные на Парето-эффективности, могут быть дополнены реальными данными и прогнозными моделями, что повышает их практическую ценность. Таким образом, несмотря на появление новых алгоритмов, подходы, связанные с многокритериальным распределением и оптимизацией по Парето, остаются востребованными, эволюционируя в сторону большей гибкости и интеграции с современными технологиями.
О Вильфредо Парето и его методе распределения по критериям
Вильфредо Парето, итальянский инженер, экономист и социолог конца XIX — начала XX века, оставил неизгладимый след в науке, сформулировав принципы, которые легли в основу современных методов оптимизации. Его работы, хотя и не всегда сразу признанные, со временем стали фундаментом для анализа эффективности в экономике, управлении и даже социальных науках. Парето родился в 1848 году в Париже, но большую часть жизни провел в Италии, где занимался исследованиями, сочетая математическую строгость с глубоким интересом к человеческому поведению. Его главный вклад — концепция «оптимальности по Парето», которая описывает состояние системы, при котором невозможно улучшить положение одного участника, не ухудшив положение другого. Эта идея стала краеугольным камнем теории благосостояния и до сих пор используется для оценки справедливости распределения ресурсов.
Однако наиболее известным наследием Парето стал эмпирический принцип, позже названный «правилом 80/20». Анализируя распределение доходов в Италии, он заметил, что 80% богатства сосредоточено в руках 20% населения. Это наблюдение, казавшееся частным случаем, оказалось универсальным: во многих сферах жизни меньшая часть усилий или ресурсов определяет большую часть результата. Например, 20% клиентов приносят 80% прибыли, 20% дефектов вызывают 80% брака, а 20% задач обеспечивают 80% продуктивности. Парето не стремился создать строгую математическую модель, но его интуиция позволила сформулировать метод приоритезации, который помогает сосредоточиться на ключевых факторах, влияющих на результат.
Интересно, что сам Парето не разрабатывал алгоритмы для практического применения своего метода. Его идеи были формализованы позже, в середине XX века, с развитием операционных исследований и теории игр. Сегодня методы, основанные на принципе Парето, используются в логистике, управлении проектами, машинном обучении и даже экологии. Например, при проектировании автомобилей инженеры ищут компромисс между стоимостью, безопасностью и топливной эффективностью, отсекая варианты, которые по всем параметрам уступают другим. В этом контексте «оптимальность по Парето» становится не абстрактной теорией, а практическим инструментом принятия решений в условиях ограниченных ресурсов и конкурирующих целей.
Критики метода отмечают, что он не дает единственного «правильного» ответа, а лишь сужает выбор. Однако в этом и заключается его сила: он признает, что в сложных системах идеального решения часто не существует, и предлагает работать с наименее противоречивыми вариантами. Парето, будучи сторонником математического подхода к социальным наукам, вероятно, одобрил бы такой прагматизм. Его метод учит, что совершенство — не всегда достижимая цель, но системный анализ позволяет приблизиться к нему, минимизируя потери.
Пример применения метода Парето для распределения бюджета
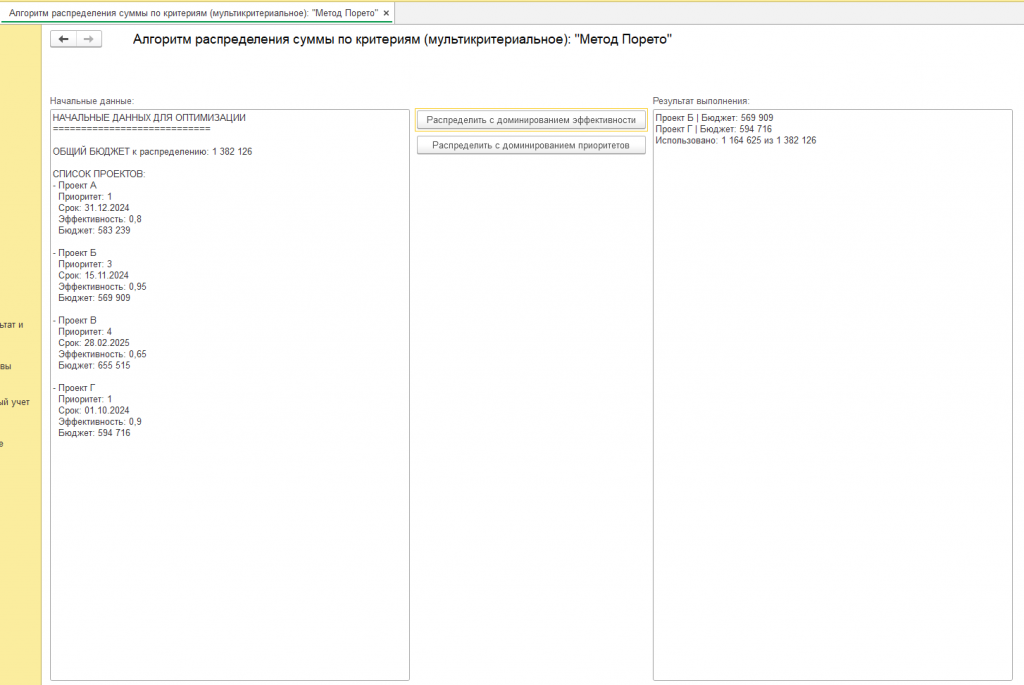
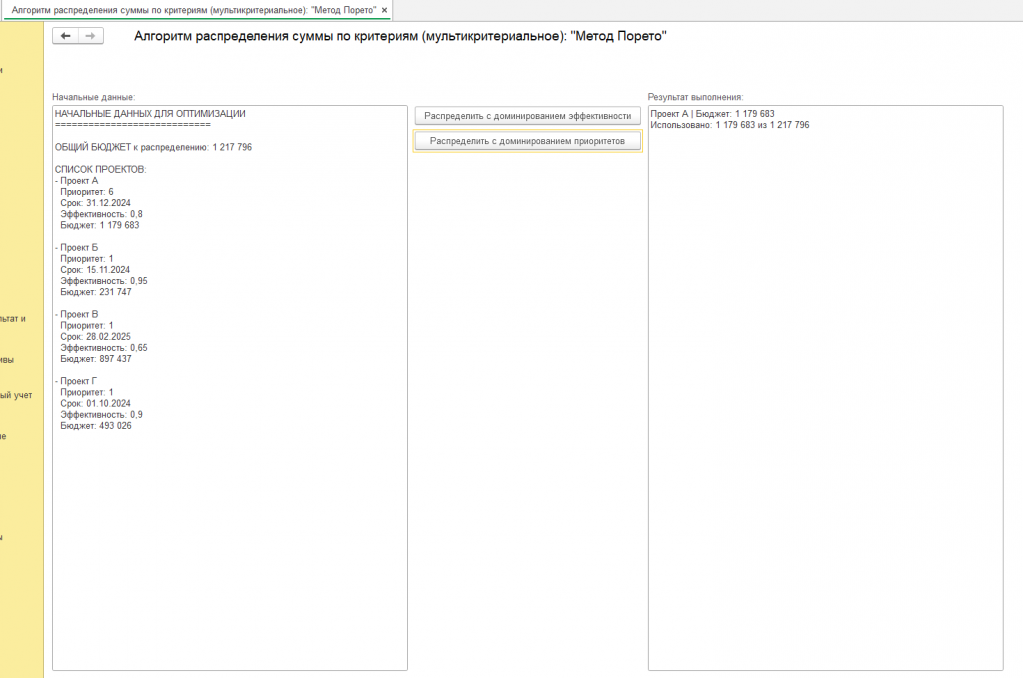
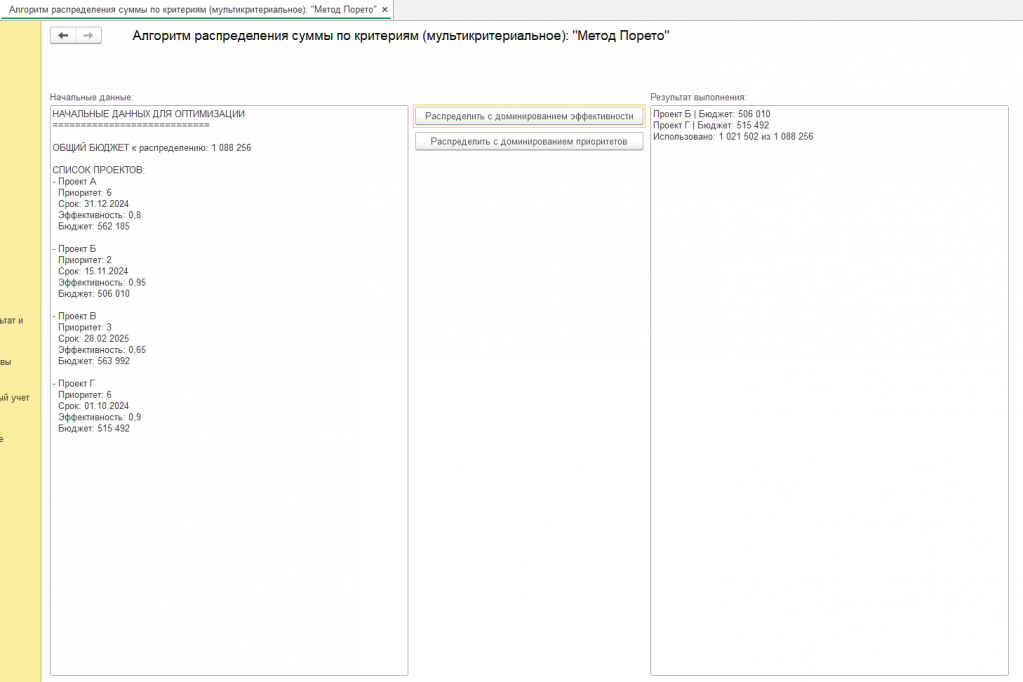
См. скриншот для наглядности с надписью "пример" (это скриншот обработки на 1с 8.3, созданной для демонстрации двух подходов метода Парето, числовые начальные данные в обработке генерируются через генератор случайных чисел, что должно привести к разным результатам метода Парето, код открыт)
Рассмотрим задачу распределения бюджета в 1 500 000 единиц между четырьмя проектами.
НАЧАЛЬНЫЕ ДАННЫХ ДЛЯ ОПТИМИЗАЦИИ
============================
ОБЩИЙ БЮДЖЕТ к распределению: 1 500 000
СПИСОК ПРОЕКТОВ:
- Проект А
Приоритет: 7
Срок: 31.12.2024
Эффективность: 0,8
Бюджет: 500 000
- Проект Б
Приоритет: 9
Срок: 15.11.2024
Эффективность: 0,95
Бюджет: 800 000
- Проект В
Приоритет: 5
Срок: 28.02.2025
Эффективность: 0,65
Бюджет: 300 000
- Проект Г
Приоритет: 8
Срок: 01.10.2024
Эффективность: 0,9
Бюджет: 600 000
Каждый проект имеет уникальные характеристики: приоритет, срок реализации, эффективность и требуемый бюджет. На первый взгляд, выбор кажется простым: достаточно отобрать проекты с максимальной эффективностью или наивысшим приоритетом. Однако метод Парето требует комплексного анализа, чтобы найти баланс между всеми критериями.
Проект Б, например, обладает самым высоким приоритетом (9) и эффективностью (0,95), но его бюджет (800 000) составляет более половины общего лимита. Если выбрать его, останется лишь 700 000, что недостаточно для реализации других значимых проектов. Проект Г, с бюджетом 600 000, имеет высокий приоритет (8) и эффективность (0,9), но его включение вместе с Проектом Б превысит бюджет. Проект А (500 000) и Проект В (300 000) менее приоритетны, но их меньшая стоимость позволяет комбинировать их с другими вариантами.
Результат обработки:
Проект В | Бюджет: 300 000
Проект А | Бюджет: 500 000
Проект Г | Бюджет: 600 000
Использовано: 1 400 000 из 1 500 000
Согласно методу Парето, оптимальным решением становится комбинация Проектов В, А и Г. Их суммарный бюджет — 1 400 000 — вписывается в лимит, а совокупная эффективность и приоритетность оказываются максимально возможными при заданных условиях. Проект В, несмотря на низкий приоритет (5), добавляет 300 000 единиц эффективности (0,65 * 300 000 = 195 000), освобождая ресурсы для более значимых инициатив. Проект А (эффективность 0,8) и Проект Г (0,9) вместе дают 1 100 000 единиц эффективности, что в сумме с Проектом В составляет 1 295 000.
Если бы вместо этого был выбран Проект Б, даже в сочетании с Проектом В, осталось бы лишь 400 000, чего недостаточно для Проекта А или Г. Это привело бы к потере более эффективных вариантов. Метод Парето исключает такие сценарии, так как они неоптимальны: включение Проекта Б ухудшает общий результат, ограничивая выбор. Кроме того, оставшиеся 100 000 из бюджета можно направить на непредвиденные расходы или мелкие задачи, что повышает гибкость планирования.
Таким образом, предложенное распределение демонстрирует, как метод Парето помогает избежать «ловушек» сиюминутной выгоды. Он учитывает не только абсолютные показатели проектов, но и их взаимное влияние в рамках системы ограничений. Это доказывает, что правильная приоритезация — это не выбор «самого лучшего», а поиск комбинации, которая приносит максимальную пользу в заданных условиях.
Другие вариации результатов смотрите на скриншотах или используйте обработку.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.20.85
Вступайте в нашу телеграмм-группу Инфостарт