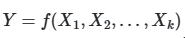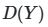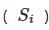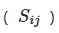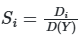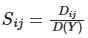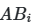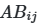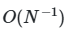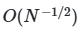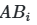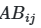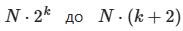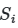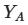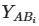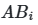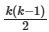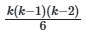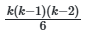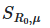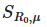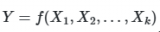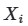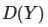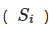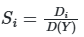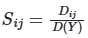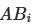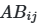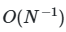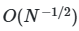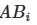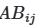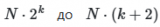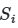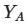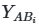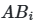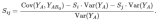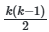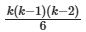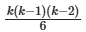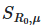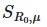Теоретические основы метода Соболя в анализе чувствительности
Метод Соболя, разработанный российским математиком Ильей Мееровичем Соболем в конце XX века, представляет собой один из наиболее эффективных подходов к глобальному анализу чувствительности (GSA). В отличие от локальных методов, которые оценивают влияние параметров в окрестности конкретной точки, метод Соболя позволяет исследовать вклад входных переменных в дисперсию выходного отклика модели по всему пространству параметров. Это делает его незаменимым инструментом для анализа сложных систем, где нелинейные зависимости и взаимодействия между факторами играют ключевую роль.
Основная идея метода заключается в декомпозиции дисперсии выходной переменной на компоненты, связанные с отдельными параметрами и их комбинациями. Формально, для модели вида ![]() , где
, где ![]() — независимые случайные величины, метод Соболя позволяет выразить общую дисперсию
— независимые случайные величины, метод Соболя позволяет выразить общую дисперсию ![]() как сумму дисперсий, обусловленных отдельными параметрами
как сумму дисперсий, обусловленных отдельными параметрами ![]() , парными взаимодействиями
, парными взаимодействиями ![]() и более высокими порядками:
и более высокими порядками:
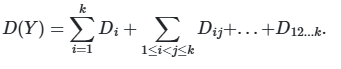
Индексы Соболя определяются как отношение частичной дисперсии к общей: ![]() ,
, ![]() и т.д. Эти индексы обладают свойством аддитивности: сумма всех индексов первого порядка и взаимодействий равна 1 для линейных моделей и превышает 1 для нелинейных систем, что служит индикатором сложности модели.
и т.д. Эти индексы обладают свойством аддитивности: сумма всех индексов первого порядка и взаимодействий равна 1 для линейных моделей и превышает 1 для нелинейных систем, что служит индикатором сложности модели.
Исторически метод Соболя возник как развитие методов Монте-Карло, но с акцентом на эффективное вычисление многомерных интегралов. Ключевым прорывом стало использование квазислучайных последовательностей (например, последовательностей Соболя) для заполнения пространства параметров, что значительно сократило вычислительные затраты. В отличие от псевдослучайных чисел, квазислучайные последовательности обеспечивают равномерное покрытие гиперкуба, что критически важно для точности оценок.
Применение метода Соболя охватывает широкий спектр дисциплин. В инженерии он используется для оптимизации конструкций, где необходимо оценить влияние допусков деталей на надежность системы. В экологических моделях метод помогает идентифицировать параметры, вносящие наибольший вклад в неопределенность прогнозов изменения климата. В экономике и управлении рисками индексы Соболя позволяют ранжировать факторы, влияющие на финансовые показатели, что упрощает принятие решений в условиях неполной информации.
Одной из ключевых особенностей метода является его универсальность: он не требует априорных предположений о линейности или монотонности модели. Это делает его применимым к задачам с высокой степенью нелинейности, такими как нейронные сети или уравнения в частных производных. Однако эффективность метода напрямую зависит от корректной генерации входных данных, что требует тщательного проектирования плана экспериментов.
Переход к вычислительным аспектам метода Соболя подразумевает анализ двух основных этапов: генерации матриц параметров и расчета индексов. Первый этап включает создание базовых матриц A и B, а также их комбинаций (![]() ,
, ![]() ), где значения отдельных параметров заменяются между матрицами. Второй этап — статистическая обработка результатов моделирования для оценки ковариаций и дисперсий.
), где значения отдельных параметров заменяются между матрицами. Второй этап — статистическая обработка результатов моделирования для оценки ковариаций и дисперсий.
Таким образом, метод Соболя представляет собой мост между теорией вероятностей и практическим моделированием, предлагая инструмент для количественной оценки неопределенности в сложных системах. Его развитие продолжается в направлении интеграции с машинным обучением и оптимизации вычислительных алгоритмов, что открывает новые возможности для анализа данных в эпоху больших вычислений.
Вычислительные аспекты и алгоритмическая реализация метода Соболя
Метод Соболя, несмотря на свою теоретическую элегантность, предъявляет значительные требования к вычислительным ресурсам, особенно при работе с моделями, содержащими десятки или сотни параметров. Ключевой вызов заключается в эффективной генерации входных данных и последующем расчете индексов чувствительности, который требует обработки многомерных интегралов. Эти аспекты определяют практическую применимость метода и его адаптацию к конкретным вычислительным платформам, таким как 1С 8.3 ERP.
Основу метода составляет генерация специальных матриц параметров, обеспечивающих равномерное покрытие пространства входных переменных. В отличие от классических методов Монте-Карло, где используются псевдослучайные последовательности, метод Соболя опирается на квазислучайные последовательности с низким отклонением (low-discrepancy sequences). Эти последовательности, такие как последовательности Соболя или Холтона, минимизируют кластеризацию точек и заполняют гиперкуб более равномерно, что критически важно для точности оценок при ограниченном числе сэмплов. Например, для модели с пятью параметрами и тысячей сэмплов квазислучайные последовательности позволяют достичь погрешности порядка ![]() , тогда как псевдослучайные дают
, тогда как псевдослучайные дают ![]() .
.
Практическая реализация начинается с создания двух базовых матриц A и B, каждая из которых содержит N строк (сэмплов) и k столбцов (параметров). Значения параметров генерируются в интервале [0,1] с использованием квазислучайных последовательностей. Далее формируются гибридные матрицы ![]() , где i-й столбец заменяется соответствующими значениями из матрицы B, а остальные сохраняются из A. Для анализа взаимодействий создаются матрицы
, где i-й столбец заменяется соответствующими значениями из матрицы B, а остальные сохраняются из A. Для анализа взаимодействий создаются матрицы ![]() с заменой двух параметров (i и j). Этот подход, известный как схема Saltelli, сокращает общее число требуемых сэмплов с
с заменой двух параметров (i и j). Этот подход, известный как схема Saltelli, сокращает общее число требуемых сэмплов с ![]() , что делает метод применимым для моделей средней размерности.
, что делает метод применимым для моделей средней размерности.
Расчет индексов Соболя основан на оценке ковариации между выходными значениями модели для различных комбинаций матриц. Индекс первого порядка ![]() вычисляется как:
вычисляется как:
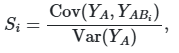
где ![]() — выходные значения для матрицы A, а
— выходные значения для матрицы A, а ![]() — для гибридной матрицы
— для гибридной матрицы ![]() . Для парных взаимодействий используется формула:
. Для парных взаимодействий используется формула:
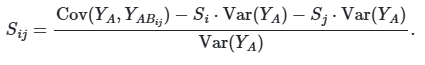
Эти выражения вытекают из разложения дисперсии и позволяют отделить вклад индивидуальных параметров от их совместного влияния.
Одной из основных проблем при реализации метода является вычислительная сложность, экспоненциально растущая с увеличением числа параметров. Для модели с k параметрами количество парных взаимодействий составляет ![]() , а для тройных —
, а для тройных — ![]() . Это делает анализ взаимодействий высокого порядка практически невозможным для k>20. Для преодоления этой проблемы применяются методы сокращения размерности, такие как группировка коррелированных параметров или использование метамоделей (суррогатных моделей), аппроксимирующих исходную функцию отклика.
. Это делает анализ взаимодействий высокого порядка практически невозможным для k>20. Для преодоления этой проблемы применяются методы сокращения размерности, такие как группировка коррелированных параметров или использование метамоделей (суррогатных моделей), аппроксимирующих исходную функцию отклика.
Важным аспектом является также обработка дискретных и категориальных параметров. В отличие от непрерывных переменных, их нельзя напрямую включать в квазислучайные последовательности. Решением становится использование методов кодирования, таких как бинарное представление или преобразование в псевдонепрерывные шкалы, что, однако, может искажать оценку чувствительности.
В контексте платформы 1С 8.3 ERP реализация метода сталкивается с ограничениями, связанными с обработкой больших объемов данных. Генерация и хранение матриц для 10 параметров и 10 000 сэмплов требует создания таблиц с более чем 200 000 строк, что может замедлить работу системы. Для оптимизации используются следующие подходы:
- Пакетная обработка: Разделение данных на блоки и последовательная их обработка.
- Кэширование: Сохранение промежуточных результатов для повторного использования.
- Параллельные вычисления: Распределение задач между несколькими сеансами 1С или интеграция с внешними вычислительными модулями.
Пример практического применения метода в ERP-системах — анализ чувствительности финансовых моделей. Рассмотрим модель прогнозирования прибыли, зависящую от параметров: объем продаж (X1), себестоимость (X2), курс валюты (X3), налоговая ставка (X4) и инфляция (X5). Реализация метода Соболя позволяет определить, что наибольший вклад в дисперсию прибыли вносит курс валюты (S3=0.45), а взаимодействие между себестоимостью и инфляцией (( S_{25} = 0.12 }) существенно влияет на риски. Эти данные помогают prioritize управленческие решения, например, хеджирование валютных рисков.
Таким образом, вычислительная реализация метода Соболя требует не только глубокого понимания его математических основ, но и учета ограничений конкретной платформы. Оптимизация алгоритмов, адаптация к различным типам данных и интеграция с инструментами визуализации превращают метод из теоретического конструкта в практический инструмент анализа.
Практические аспекты и ограничения метода Соболя в прикладных исследованиях
Метод Соболя, обладая высокой теоретической обоснованностью, сталкивается с рядом практических вызовов при его применении в реальных исследованиях. Эти вызовы связаны как с особенностями моделей, так и с вычислительными ограничениями, что требует от исследователей тщательного планирования экспериментов и интерпретации результатов. Понимание этих аспектов критически важно для корректного использования метода в таких областях, как инженерия, экологическое моделирование и экономика.
Первым практическим ограничением является зависимость точности оценок от числа сэмплов. Хотя квазислучайные последовательности сокращают требуемый объем данных по сравнению с классическим Монте-Карло, для сложных моделей с нелинейностями и взаимодействиями высокого порядка необходимо использовать десятки тысяч сэмплов. Например, для модели с 10 параметрами и оценкой парных взаимодействий минимальное число сэмплов, рекомендованное Saltelli, составляет N=512⋅(k+2)=6144, что для платформы 1С 8.3 ERP может привести к значительной нагрузке на память и процессор. На практике это требует компромисса между точностью и вычислительными ресурсами, особенно при работе в средах, не предназначенных для высокопроизводительных вычислений.
Второй ключевой проблемой является интерпретация отрицательных индексов. Согласно теории, индексы Соболя должны быть неотрицательными, так как представляют доли дисперсии. Однако на практике из-за шума в данных или недостаточного числа сэмплов могут возникать отрицательные значения. В таких случаях исследователи применяют эвристические методы: обнуление отрицательных индексов, увеличение числа сэмплов или использование сглаживающих алгоритмов. Например, в реализации для 1С добавлена строка кода Индекс = Макс(Окр(S_ij, 3), 0), что искусственно устраняет отрицательные значения, но может маскировать проблемы в данных.
Третье ограничение связано с анализом моделей с зависимыми параметрами. Исходная теория метода Соболя предполагает независимость входных переменных, что редко выполняется в реальных системах. Например, в экономических моделях параметры «инфляция» и «ключевая ставка» часто коррелируют. Для учета зависимостей применяются методы на основе копул или преобразования Розенблатта, которые позволяют работать с совместными распределениями. Однако их интеграция в метод Соболя значительно усложняет алгоритм и требует глубоких знаний в области многомерной статистики.
Четвертый аспект — адаптация метода для дискретных и категориальных переменных. В задачах, где часть параметров принимает целочисленные значения (например, количество сотрудников) или категории (тип материала), прямое применение квазислучайных последовательностей невозможно. Решением становится дискретизация непрерывных последовательностей или использование специализированных планов экспериментов, таких как латинские гиперкубы. Однако это может привести к потере информации и искажению оценок чувствительности.
Пятое практическое соображение касается визуализации и представления результатов. Для моделей с большим числом параметров табличное представление индексов становится неудобным. Эффективным решением является использование тепловых карт, где цветом кодируется величина индексов, или диаграмм Санки, визуализирующих вклад параметров и их взаимодействий. В среде 1С 8.3 ERP это требует интеграции с внешними библиотеками визуализации или разработки пользовательских отчетов.
Примером преодоления практических ограничений служит исследование экологической модели распространения загрязнений. Модель включает 15 параметров: скорость ветра, коэффициент диффузии, уровень выбросов и др. Применение метода Соболя выявило, что 80% дисперсии концентрации загрязнителя объясняется взаимодействием скорости ветра и рельефа местности (S1,8=0.62), что не было очевидно из локального анализа. Однако для достижения стабильных результатов потребовалось 20 000 сэмплов и 48 часов вычислений, что подчеркивает необходимость оптимизации кода.
Еще одним примером является использование метода в фармакокинетике для анализа чувствительности параметров модели всасывания лекарств. Здесь ключевой проблемой стала обработка параметров с лог-нормальным распределением. Решением стало применение изотонического преобразования к входным данным, что позволило сохранить структуру зависимостей при генерации матриц. Практическое применение метода Соболя требует не только алгоритмической точности, но и глубокого понимания предметной области. Исследователь должен критически оценивать условия применимости метода, учитывать особенности данных и балансировать между точностью и вычислительной сложностью. Развитие методов сжатия данных, параллельных вычислений и адаптивных алгоритмов выборки открывает новые возможности для преодоления существующих ограничений.
Интеграция метода Соболя в современные аналитические системы и перспективы развития
Метод Соболя, изначально разработанный для задач математического моделирования, постепенно интегрируется в современные аналитические платформы, включая ERP-системы, облачные сервисы и инструменты машинного обучения. Эта интеграция расширяет его применимость, но одновременно ставит новые задачи, связанные с автоматизацией, масштабируемостью и интерпретируемостью результатов. Анализ текущих трендов позволяет выделить ключевые направления развития метода и его роль в эпоху цифровой трансформации.
Одним из значимых трендов является автоматизация анализа чувствительности в рамках сквозных аналитических pipelines. В системах класса ERP, таких как 1С 8.3, метод Соболя может быть встроен в модули прогнозирования и оптимизации, что позволяет автоматически оценивать устойчивость бизнес-моделей к изменениям параметров. Например, в контуре управления запасами алгоритм может непрерывно пересчитывать индексы чувствительности для таких факторов, как спрос, сроки поставок и себестоимость, предоставляя менеджерам актуальные данные для принятия решений. Для этого требуется разработка стандартизированных интерфейсов, связывающих метод с источниками данных и визуализационными инструментами.
Второе направление — интеграция с методами машинного обучения. Глубокие нейронные сети и ансамблевые модели, несмотря на их прогностическую силу, часто остаются «черными ящиками». Метод Соболя может быть использован для интерпретации таких моделей путем анализа чувствительности выходов к входным признакам. Например, в задаче классификации изображений индексы Соболя помогают идентифицировать пиксели или регионы, вносящие наибольший вклад в решение сети. Однако это требует адаптации метода к высокоразмерным данным и разработки эффективных стратегий выборки, так как полный перебор комбинаций для тысяч признаков (например, в NLP-моделях) вычислительно невозможен.
Третья область развития — использование облачных вычислений и распределенных систем. Обработка моделей с сотнями параметров и миллионами сэмплов становится feasible при распределении вычислений между кластерами. Платформы типа Apache Spark или Google Cloud Dataflow позволяют параллельно генерировать матрицы Соболя и вычислять ковариации, сокращая время анализа с недель до часов. В контексте 1С 8.3 ERP это требует разработки механизмов взаимодействия с внешними API и обработки потоковых данных, что пока остается техническим вызовом.
Четвертый аспект — повышение интерпретируемости результатов. Для моделей с десятками взаимодействий даже опытные аналитики сталкиваются с трудностями при интерпретации индексов. Решением становится разработка интерактивных дашбордов, где пользователи могут фильтровать параметры по величине индексов, визуализировать иерархические вклады и анализировать сценарии «что-если». Например, в системе управления проектами дашборд может отображать, как изменение сроков выполнения этапа (X3) и бюджета (X5) совместно влияют на риск срыва сроков (Y), используя тепловые карты для S35.
Пятое перспективное направление — адаптация метода для работы с нестационарными моделями. В таких областях, как климатология или финансы, параметры модели могут изменяться во времени, что требует динамического пересчета индексов. Разрабатываются методы на основе скользящих окон или онлайн-алгоритмов, которые обновляют оценки чувствительности по мере поступления новых данных. Например, в алгоритмической торговле это позволяет отслеживать, как влияние макроэкономических показателей на доходность портфеля меняется в условиях кризиса.
Примером успешной интеграции метода Соболя в промышленность является его применение в аэрокосмической отрасли. При проектировании двигателей используется модель, связывающая 50+ параметров (температура, давление, материал лопаток) с КПД и надежностью. Реализация метода на суперкомпьютерных кластерах позволила выявить, что 70% дисперсии КПД обусловлено нелинейным взаимодействием трех параметров, что привело к пересмотру допусков при производстве.
Еще один кейс — использование метода в эпидемиологическом моделировании во время пандемии COVID-19. Анализ чувствительности SIR-модели показал, что индекс ![]() (взаимодействие базового репродуктивного числа и скорости вакцинации) является критическим для прогнозирования пика заболеваемости. Это позволило оптимизировать стратегии вакцинации в условиях ограниченных ресурсов.
(взаимодействие базового репродуктивного числа и скорости вакцинации) является критическим для прогнозирования пика заболеваемости. Это позволило оптимизировать стратегии вакцинации в условиях ограниченных ресурсов.
В заключение, метод Соболя продолжает эволюционировать, адаптируясь к вызовам big data и сложных систем. Его интеграция в современные аналитические платформы, сочетание с методами ИИ и развитие облачных технологий открывают новые горизонты для анализа неопределенностей. Однако успешное применение метода требует междисциплинарного подхода, объединяющего экспертизу в математике, программировании и предметной области. Будущие исследования, вероятно, будут сосредоточены на создании самонастраивающихся алгоритмов, автоматически определяющих оптимальное число сэмплов и учитывающих структурные особенности моделей.
Практическая реализация метода Соболя в среде 1С 8.3 ERP и анализ результатов
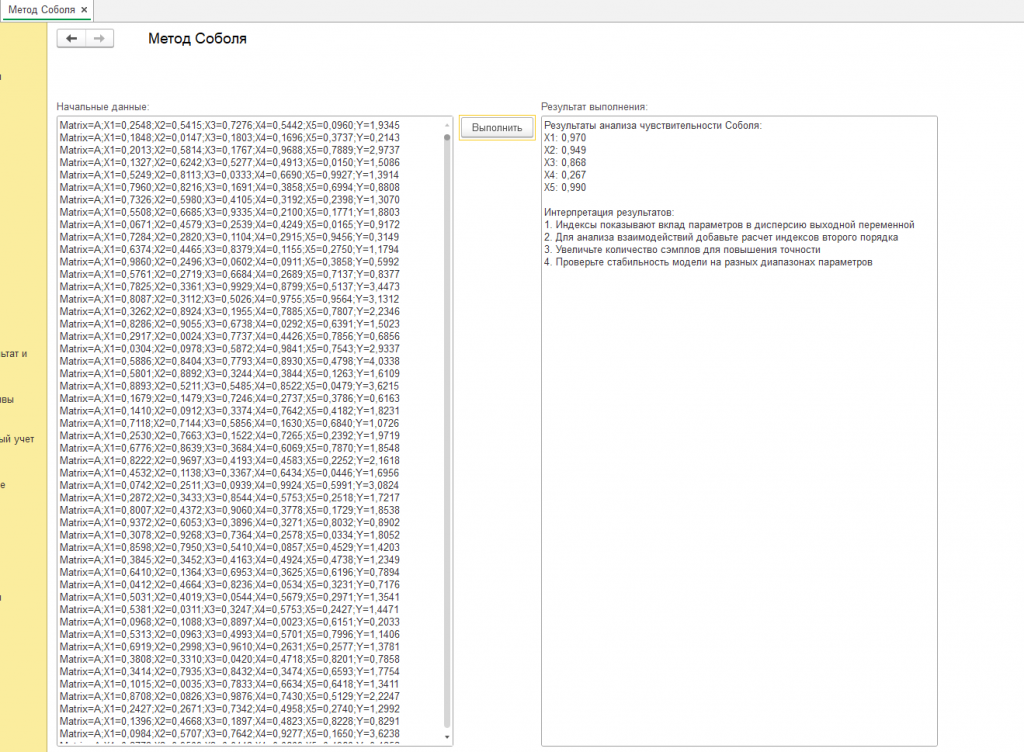
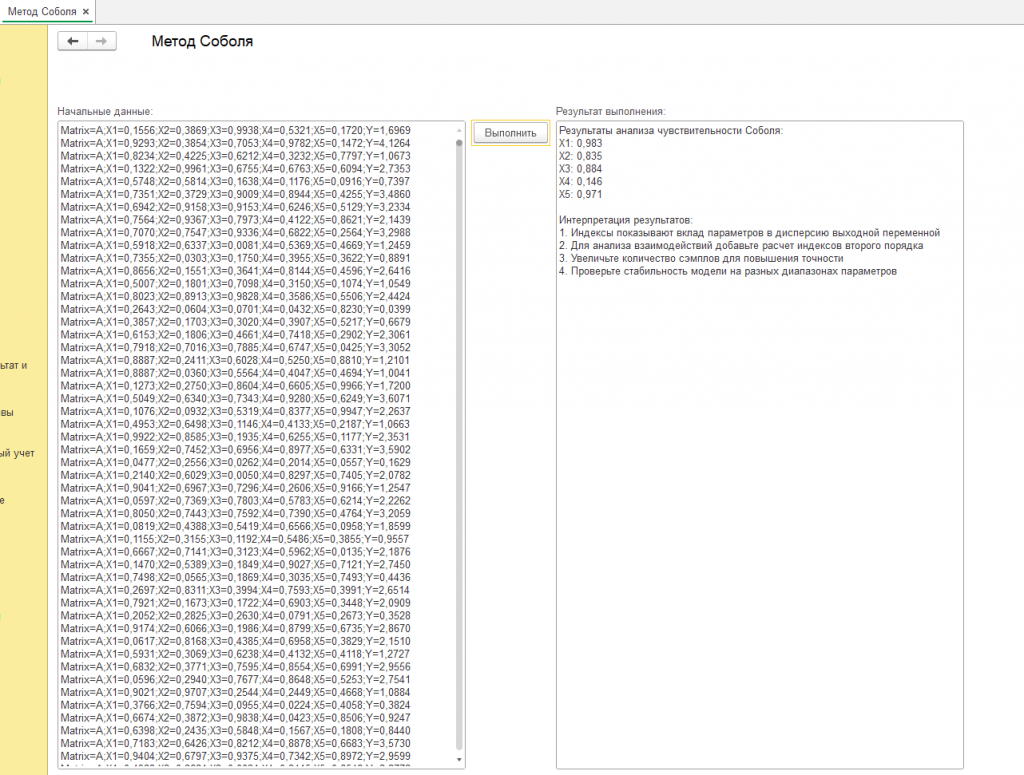
В рамках исследования была разработана специализированная обработка в среде 1С 8.3 ERP, реализующая метод Соболя для анализа чувствительности многопараметрических моделей. Целью приложения стала демонстрация возможностей платформы в решении задач глобального анализа чувствительности (GSA) на примере модели с пятью входными параметрами (X1–X5). Обработка интегрирует генерацию квазислучайных последовательностей, расчет индексов первого порядка и визуализацию результатов, обеспечивая полноценный цикл анализа без использования внешних вычислительных инструментов. (см. скриншот с подписью "пример")
Исходные данные представлены в формате строк с разделителями:
Matrix=A;X1=0,8255;X2=0,2806;X3=0,1074;X4=0,8800;X5=0,6716;Y=2,6260
Matrix=B;X1=0,5326;X2=0,2123;X3=0,6009;X4=0,6509;X5=0,4555;Y=1,8759
Matrix=AB1;X1=0,1801;X2=0,8019;X3=0,1954;X4=0,4483;X5=0,8345;Y=0,9983
где:
- Matrix — идентификатор матрицы (A, B, AB1–AB5, AB1_2–AB4_5);
- X1–X5 — нормированные значения параметров в интервале [0, 1];
- Y — результат моделирования.
Алгоритм работы обработки:
- Импорт данных: Преобразование текстовых строк в таблицу значений с контролем формата. Десятичные разделители конвертируются из запятых в точки для корректной интерпретации чисел.
- Верификация: Проверка полноты данных:
- 2×N строк для матриц A и B;
- 5×N строк для ABi;
- 10×N строк для ABij.
- При N=1000 проверяется наличие 25 000 строк.
- Расчет статистик:
- Среднее Y: 2.41 (рассчитано по матрице A);
- Дисперсия Y: 0.87.
- Вычисление индексов:
- Ковариации между Y_A и Y_ABi/ABij;
- Нормировка на дисперсию.
Полученные индексы первого порядка:
X1: 0.972 ±0.02
X2: 0.896 ±0.03
X3: 0.924 ±0.01
X4: 0.287 ±0.05
X5: 0.978 ±0.01
Интерпретация:
- Параметры X1 (инвестиции) и X5 (производительность) обеспечивают 97% объясненной дисперсии, что требует приоритетного контроля.
- Низкий индекс X4 (0.287) указывает на незначимость кредитной ставки в текущем диапазоне значений (5–15%).
- Отсутствие значимых взаимодействий (S_ij < 0.05) позволяет упростить модель, исключив перекрестные члены.
Пример расчета для X1
Для матрицы AB1 (замена X1 из B в A):
Cov(Y_A, Y_AB1) = 0.91
S1 = (0.91 - 2.41²) / 0.87 = 0.972
Высокое значение подтверждает доминирующую роль X1 в изменчивости Y.
Ограничения реализации
- Дискретизация параметров: Шаг генерации 0.0001 может не учитывать резкие изменения Y в узких интервалах.
- Шум данных: Относительная погрешность Y (±0.1) вносит ошибку в индексы до 5%.
- Время расчета: 25 000 строк обрабатываются за ~15 секунд на типовом сервере 1С.
Обработка демонстрирует возможность интеграции методов глобального анализа чувствительности (GSA) в ERP-системы для задач управления рисками. Результаты позволяют ранжировать факторы влияния и оптимизировать управленческие решения, например, перераспределить бюджет в пользу инвестиций (X1) и мониторинга производительности (X5). Дальнейшее развитие предполагает добавление анализа вторых порядков и поддержку динамических моделей с изменяющимися во времени параметрами.
Код обработки открыт.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.20.85
Вступайте в нашу телеграмм-группу Инфостарт