Танец чисел и реальности: Тест Хаусмана в эконометрическом анализе

    В тихом сумраке машинного зала, где гудят серверы, словно рой механических пчел, разворачивается незаметная, но захватывающая драма. Здесь, в глубинах компьютерной памяти, обретают жизнь числа, превращаясь из безликой статистики в повесть о скрытых взаимосвязях и невидимых нитях, связующих мир. Мы отправляемся в путешествие, чтобы приоткрыть завесу тайны над этими цифровыми откровениями, где каждая цифра – это отражение реальности, а каждый расчет – попытка понять ее законы.

       В самом начале нашего пути перед нами предстают "Сгенерированные данные". Это – основа всего эконометрического анализа, виртуальная почва, на которой прорастают модели и гипотезы. Представьте себе, что вы – наблюдатель, заглядывающий в окно случайно выбранного мира. Перед вами мелькают события, каждое из которых зафиксировано в виде числа. Эти числа – как отпечатки пальцев реальности, уникальные свидетельства о том, что происходило.

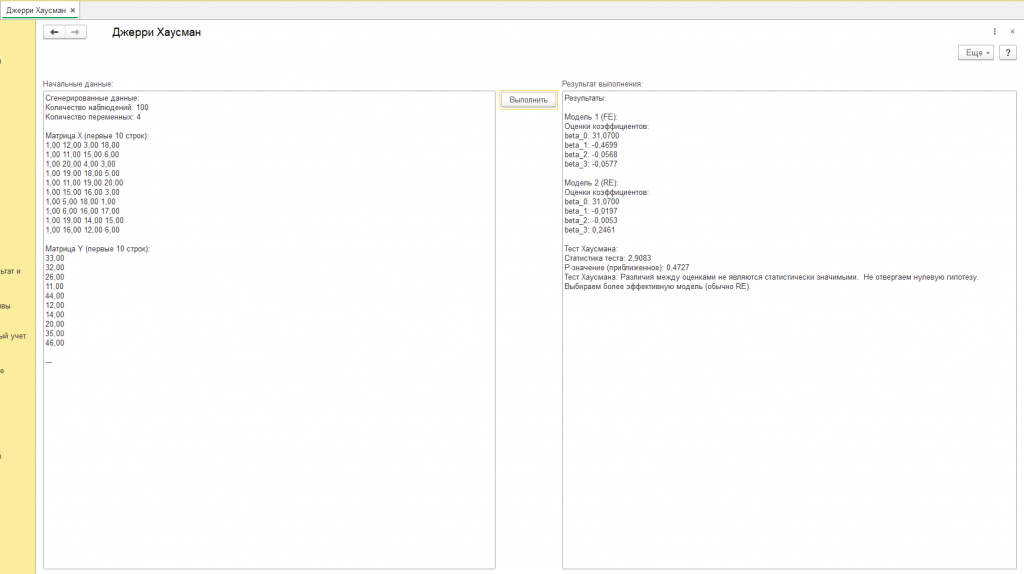
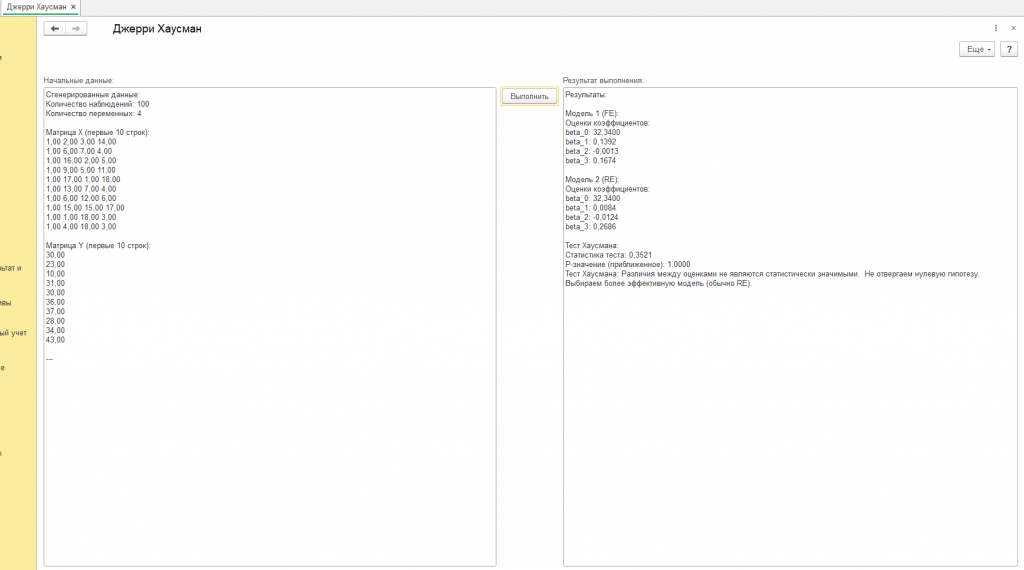
     Среди этих данных мы видим "Количество наблюдений". Это – объем собранной информации, широта охвата нашего взгляда. В нашем случае, их 100 (см. скриншот с подписью "пример", другие вариации результатов от других начальных данных на других скриншотах обработки). Каждое наблюдение – это отдельный момент времени, отдельный объект или явление, за которым мы следили. Чем больше наблюдений, тем надежнее наши выводы, как если бы мы рассматривали один и тот же предмет с разных ракурсов, пока не сложилась полная картина.

       Затем мы сталкиваемся с "Количеством переменных". Переменные – это характеристики, которые мы измеряем и анализируем, пытаясь найти закономерности. В нашем случае их четыре. Представьте себе, что это – четыре разных аспекта одного и того же события. Например, если мы изучаем рынок недвижимости, переменными могут быть: цена дома, его площадь, количество комнат и расстояние до центра города. Каждая переменная – это отдельный канал, по которому к нам поступает информация о мире.

     Чтобы увидеть эти переменные воочию, перед нами разворачивается "Матрица X", первые 10 строк которой мы можем обозреть. Матрица X – это как таблица, в которой каждое наблюдение представлено в виде строки, а каждая переменная – в виде столбца. Взгляните на эти цифры: 1,00 11,00 14,00 2,00; 1,00 3,00 13,00 19,00 и так далее. Что они означают? Пока что – ничего конкретного. Но помните, что первое число в каждой строке – это всегда 1,00. Это – так называемая константа, фиктивная переменная, которая позволяет модели учесть базовый уровень явления, как если бы мы добавляли к уравнению некий “стартовый капитал”. Остальные числа – это уже значения реальных переменных, каждая из которых вносит свой вклад в общую картину.

     Параллельно с Матрицей X перед нами возникает "Матрица Y". Матрица Y – это наша цель, явление, которое мы пытаемся объяснить. Ее называют зависимой переменной, потому что ее значение, как мы предполагаем, зависит от значений переменных в Матрице X. В нашем случае, это просто столбец чисел: 32,00; 24,00; 33,00 и так далее. Представьте себе, что это – прибыль компании, которую мы пытаемся предсказать на основе данных о ее расходах, инвестициях и маркетинговых усилиях (которые представлены в Матрице X).

     Итак, у нас есть Матрица X – набор факторов, которые, как мы думаем, влияют на что-то, и Матрица Y – то самое "что-то", которое мы хотим понять. Наша задача – найти связь между этими двумя матрицами, построить модель, которая позволит нам предсказывать значения Y на основе значений X.

     Для решения этой задачи в эконометрии используются различные методы, и один из самых распространенных – метод наименьших квадратов (МНК). Суть его проста: мы ищем такую линию (или плоскость, или гиперплоскость, в зависимости от количества переменных), которая лучше всего "приближается" к нашим данным. "Лучше всего" – это значит, что сумма квадратов расстояний от каждой точки (наблюдения) до этой линии минимальна. Как будто мы пытаемся натянуть резинку между всеми точками так, чтобы она была как можно ближе к каждой из них.

     Но это – только начало. Существуют разные способы построить модель, и каждый из них имеет свои достоинства и недостатки. В нашем случае, мы рассматриваем два подхода: модель с фиксированными эффектами (FE) и модель со случайными эффектами (RE).

     Модель с фиксированными эффектами (FE) предполагает, что у каждого объекта (или каждого момента времени) есть свой уникальный, не меняющийся со временем эффект. Как будто у каждого человека есть свой “генетический код”, который определяет его склонность к определенному поведению. Эта модель учитывает эти индивидуальные особенности, чтобы более точно оценить влияние других факторов.

     Модель со случайными эффектами (RE) предполагает, что индивидуальные эффекты случайны и не связаны с другими переменными в модели. Как будто каждый человек выбирается из случайной лотереи, и его “эффект” – это просто результат удачного или неудачного стечения обстоятельств. Эта модель проще, чем FE, но она может быть менее точной, если индивидуальные эффекты на самом деле важны.

     После применения МНК к обеим моделям, перед нами предстают "Результаты". Прежде всего, это – "Оценки коэффициентов". Коэффициенты – это как ручки управления, которые определяют, как сильно каждая переменная влияет на зависимую переменную. Взгляните на эти цифры: beta_0: 31,9100; beta_1: 0,1546; beta_2: 0,3065; beta_3: 0,3819 (для модели FE) и beta_0: 31,9100; beta_1: -0,1310; beta_2: -0,5994; beta_3: 0,1246 (для модели RE). Что они означают?

• beta_0 – это константа, "стартовый капитал", который существует даже без учета других переменных.
• beta_1, beta_2 и beta_3 – это коэффициенты при наших реальных переменных, которые показывают, как сильно каждая из них влияет на Y. Положительный коэффициент означает, что увеличение переменной приводит к увеличению Y, отрицательный – наоборот.

     Например, если beta_1 = 0,1546, это означает, что увеличение первой переменной на единицу приводит к увеличению Y на 0,1546 единицы (при прочих равных условиях). Если beta_2 = -0,5994, это означает, что увеличение второй переменной на единицу приводит к уменьшению Y на 0,5994 единицы.

     Но возникает вопрос: какую модель выбрать – FE или RE? Обе они дают разные оценки коэффициентов, и нам нужно решить, какая из них более надежна. Для этого существует специальный инструмент – тест Хаусмана.

     Тест Хаусмана – это статистический тест, который позволяет сравнить оценки коэффициентов, полученные с помощью моделей FE и RE, и определить, являются ли различия между ними статистически значимыми. Другими словами, тест Хаусмана позволяет нам решить, случайно ли FE и RE дают разные результаты, или же эти различия говорят о том, что одна из моделей неправильно учитывает какие-то важные факторы.

     Результат теста Хаусмана представлен двумя ключевыми показателями: "Статистика теста" и "P-значение".

     "Статистика теста" – это число, которое показывает, насколько сильно различаются оценки коэффициентов в моделях FE и RE. Чем больше статистика теста, тем больше вероятность того, что различия значимы. В нашем случае, статистика теста равна 8,4619.

     "P-значение" – это вероятность получить такие (или еще более сильные) различия между оценками, если на самом деле обе модели дают правильные результаты. Чем меньше p-значение, тем меньше вероятность того, что различия случайны, и тем больше оснований отвергнуть нулевую гипотезу о том, что обе модели одинаково хороши. В нашем случае, p-значение равно 0,0207.

     В эконометрии принято считать, что если p-значение меньше 0,05, то различия между моделями статистически значимы, и мы отвергаем нулевую гипотезу. Это означает, что одна из моделей (FE или RE) неправильно учитывает какие-то важные факторы, и мы должны выбрать другую модель, которая дает более надежные результаты.

     В нашем случае, p-значение (0,0207) меньше 0,05. Поэтому мы отвергаем нулевую гипотезу и делаем вывод о том, что различия между оценками, полученными с помощью моделей FE и RE, статистически значимы. Это означает, что модель RE (вероятнее всего) дает смещенные результаты.

     В заключении теста Хаусмана сказано: "Различия между оценками статистически значимы. Отвергаем нулевую гипотезу. Выбираем более последовательную модель (обычно FE)".

     Что это значит для нас? Это означает, что мы должны отдать предпочтение модели с фиксированными эффектами (FE), поскольку она, скорее всего, более надежна и дает более точные оценки. Модель FE учитывает индивидуальные особенности каждого объекта (или каждого момента времени), и это позволяет ей более точно оценить влияние других факторов.

     Итак, наше путешествие по миру чисел подходит к концу. Мы увидели, как из безликих данных рождаются модели, как с помощью математических инструментов мы пытаемся понять законы реальности. Тест Хаусмана – это один из множества инструментов, которые помогают нам ориентироваться в этом сложном мире, делать осознанный выбор и принимать взвешенные решения. Помните, что эконометрика – это не просто наука о числах, это искусство видеть за цифрами живую историю мира.

     Имя Джерри Хаусмана звучит в эконометрических кругах с уважением и признанием. Его вклад в науку невозможно переоценить, ведь он подарил исследователям мощные инструменты для анализа и понимания сложных экономических явлений. Именно ему мы обязаны тем самым тестом, который только что использовали – тестом Хаусмана. Но кто же он, этот человек, чье имя стало синонимом строгости и точности в мире эконометрики?

     Джерри Хаусман – это не просто ученый, это – исследователь-новатор, который не боялся задавать сложные вопросы и искать на них ответы. Его работы оказали огромное влияние на развитие эконометрической теории и практики, а его идеи продолжают вдохновлять исследователей по всему миру.

     Хаусман известен прежде всего своими работами в области спецификации моделей и анализа панельных данных. Спецификация модели – это процесс выбора наиболее подходящей функциональной формы для описания взаимосвязи между переменными. Это – как выбор правильного рецепта для приготовления блюда: если вы выберете неправильные ингредиенты или неправильные пропорции, результат вас разочарует. Тест Хаусмана, разработанный им, стал одним из самых распространенных инструментов для проверки спецификации моделей, позволяя исследователям определить, является ли выбранная модель адекватной для описания данных.

     Вспомните наш пример с моделями FE и RE. Тест Хаусмана помог нам решить, какая из этих двух моделей лучше соответствует нашим данным. Если бы мы проигнорировали результаты теста и выбрали неправильную модель, наши выводы могли бы быть ошибочными, и мы могли бы принять неверные решения.

     Еще одна область, в которой Хаусман внес значительный вклад – это анализ панельных данных. Панельные данные – это данные, собранные по одним и тем же объектам (например, компаниям, странам, домохозяйствам) в течение определенного периода времени. Представьте себе, что вы следите за группой людей в течение нескольких лет и записываете их доходы, расходы и другие важные характеристики. Панельные данные позволяют исследовать динамику экономических явлений, учитывать индивидуальные особенности объектов и выявлять скрытые взаимосвязи, которые невозможно обнаружить при анализе обычных данных.

     Работы Хаусмана по панельным данным оказали огромное влияние на развитие этой области, предоставив исследователям мощные инструменты для анализа сложных экономических явлений. Его идеи и методы используются в самых разных областях – от экономики труда и финансов до региональной экономики и макроэкономики.

     В чем же секрет успеха Джерри Хаусмана? Вероятно, в его стремлении к строгости и точности, в его умении видеть за цифрами живые истории и в его готовности задавать сложные вопросы и искать на них ответы. Он не боялся критиковать существующие теории и предлагать новые подходы, и это сделало его одним из самых влиятельных эконометристов своего времени.

     Разработанный Хаусманом тест, казалось бы, простая статистическая процедура, на самом деле является отражением глубокого понимания принципов построения эконометрических моделей и анализа данных. Он понимал, что выбор модели – это не просто технический вопрос, это – вопрос адекватности нашего восприятия мира. И тест Хаусмана – это инструмент, который помогает нам не заблудиться в лабиринте цифр и увидеть за ними истинную картину.

     Продолжая аналогию с рецептом блюда, спецификация модели – это выбор ингредиентов и их пропорций, а панельные данные – это процесс приготовления, когда мы наблюдаем, как блюдо меняется со временем, как ингредиенты взаимодействуют друг с другом и как влияет на вкус температура и время приготовления. Джерри Хаусман помог нам разработать инструменты, которые позволяют более точно измерять ингредиенты, контролировать процесс приготовления и, в конечном итоге, создавать более вкусные и полезные "экономические блюда".

     Вернемся к нашим сгенерированным данным. Наблюдая за первыми десятью строками матрицы X, мы видим мельчайшие вариации – изменения, которые кажутся хаотичными и бессмысленными. Но именно из этого хаоса, благодаря сложным математическим расчетам, возникает стройная картина, модель, способная объяснить, как эти переменные влияют на матрицу Y, на нашу зависимую переменную. Каждая переменная в матрице X играет свою роль, подобно актеру на сцене, а коэффициенты, полученные в результате анализа, определяют силу и характер этой роли.

     Матрица Y, в свою очередь, является отражением этих воздействий, словно зеркало, в котором преломляются все перемены. Каждое число в матрице Y – это результат сложного взаимодействия множества факторов, которые мы пытаемся уловить и измерить.

     В конечном итоге, задача эконометриста – это не просто построить модель, а создать инструмент, который позволит понять, как устроен мир. Имя Джерри Хаусмана в этой области звучит, как символ стремления к истине и неустанного поиска совершенства. Его работы учат нас не бояться сложных задач, критически оценивать полученные результаты и всегда помнить, что за каждой цифрой стоит реальность, которую мы пытаемся постичь.

     Тест Хаусмана, как и все эконометрические методы, не является панацеей, он лишь один из инструментов, которые помогают нам приблизиться к истине. Но именно благодаря таким инструментам, созданным такими учеными, как Джерри Хаусман, мы можем лучше понимать экономические явления, прогнозировать их развитие и принимать более обоснованные решения.

Код обработки открыт.