Анализ временного ряда: Поиск скрытых закономерностей
В современном мире, где информация льется рекой, умение анализировать данные становится все более ценным. Одним из важнейших видов данных являются временные ряды – последовательности значений, измеренных в разные моменты времени. Они окружают нас повсюду: от графиков температуры и цен на акции до статистики продаж и посещаемости сайтов. Анализ временных рядов позволяет выявлять закономерности, делать прогнозы и принимать обоснованные решения.
Целью данной работы является демонстрация базовых методов анализа временного ряда на примере случайного набора данных. Мы не будем углубляться в сложные математические формулы и термины, а постараемся объяснить основные принципы простым и понятным языком. Представьте, что мы пытаемся прочитать книгу, написанную на незнакомом языке. Наша задача – понять хотя бы общий смысл, выявить основные сюжетные линии.
Что такое временной ряд?
Представьте себе журнал, в котором вы каждый день записываете какие-то значения. Это может быть количество выпитого кофе, пройденные шаги, настроение по шкале от 1 до 10. Каждая запись в журнале – это значение временного ряда, а дата записи – это момент времени. Вместе они образуют последовательность данных, которая рассказывает историю изменений во времени.
Временной ряд может представлять практически любой процесс, который изменяется во времени. К примеру, взглянем на экономику. Здесь мы увидим курс валют, уровень инфляции, Валовой Внутренний Продукт (ВВП), объемы продаж различных товаров, а также статистику о количестве безработных. Все это - примеры временных рядов, отражающих состояние и динамику экономических процессов. А если мы обратимся к сфере финансов, то обнаружим цены на акции, объемы торгов на биржах и процентные ставки банков. Эти данные, зафиксированные во времени, позволяют анализировать финансовые рынки и принимать инвестиционные решения.
Не менее важны временные ряды и в метеорологии. Ежедневные измерения температуры воздуха, количества осадков, влажности и скорости ветра позволяют ученым изучать климатические изменения и составлять прогнозы погоды. В сфере транспорта, данные о пассажиропотоке, загруженности дорог и количестве дорожно-транспортных происшествий помогают оптимизировать транспортные потоки и повышать безопасность на дорогах.
Здравоохранение также активно использует временные ряды для анализа заболеваемости, смертности и загруженности медицинских учреждений, что позволяет эффективно планировать ресурсы и разрабатывать стратегии борьбы с эпидемиями. Наконец, даже в интернете мы сталкиваемся с временными рядами в виде статистики посещаемости сайтов, количества поисковых запросов и активности пользователей в социальных сетях. Эти данные позволяют компаниям анализировать поведение потребителей и оптимизировать свои онлайн-стратегии.
Анализ временных рядов позволяет отвечать на важные вопросы. Мы можем узнать, какие тенденции наблюдаются в данных, есть ли сезонные колебания, как значения связаны между собой в разные моменты времени, и, самое главное, можно ли предсказать будущие значения. Эти вопросы крайне важны для принятия обоснованных решений в самых разных областях.
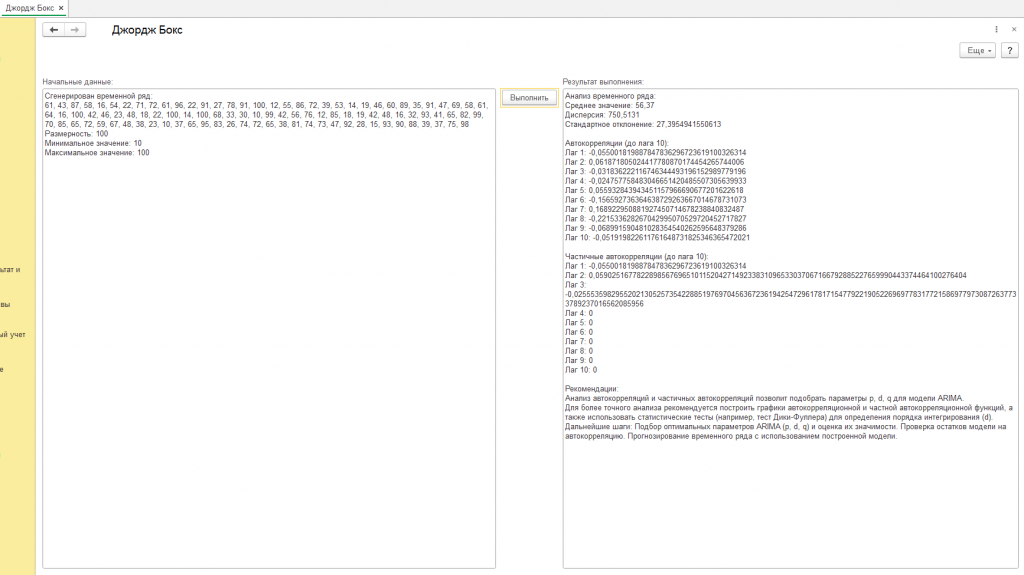
Наш пример: Случайный временной ряд (см. скриншот с подписью "пример")
Для демонстрации методов анализа мы будем использовать искусственно созданный временной ряд. Представьте, что у нас есть генератор случайных чисел – программа, которая выдает случайные числа в заданном диапазоне. Мы попросили ее сгенерировать 100 чисел в диапазоне от 10 до 100. Полученная последовательность чисел и будет нашим временным рядом.
Почему случайный? Потому что на его примере хорошо видны основные принципы анализа, без отвлечения на сложные закономерности реальных данных. Это как азбука – начинаем с простых букв, чтобы потом читать сложные слова.
Сгенерированные числа можно увидеть в разделе “Начальные данные”. Это просто набор цифр, но даже в них можно найти кое-что интересное.
Базовые характеристики: О чем говорят числа
Первым шагом в анализе временного ряда является расчет базовых статистических характеристик. Они помогают получить общее представление о данных, понять их основные свойства.
Представьте, что мы хотим найти “типичное” значение в нашем временном ряду. Для этого мы складываем все числа и делим на их количество. Полученное значение называется средним. В нашем примере среднее значение равно 55.95. Это означает, что большинство чисел находятся где-то около этой отметки. Среднее значение показывает, вокруг какого уровня колеблются данные.
Теперь представим, что мы хотим узнать, насколько сильно числа отклоняются от среднего значения. Для этого мы вычисляем дисперсию. Она показывает, насколько сильно разбросаны данные относительно среднего. Чем больше дисперсия, тем больше разброс. В нашем примере дисперсия равна 626.35. Это говорит о том, что числа довольно сильно отличаются друг от друга.
Дисперсия – это полезный показатель, но его не всегда удобно интерпретировать. Поэтому часто используют стандартное отклонение – квадратный корень из дисперсии. Оно показывает, на какое расстояние в среднем числа отклоняются от среднего значения. В нашем примере стандартное отклонение равно 25.03. Это означает, что типичное значение отклоняется от среднего примерно на 25 единиц.
Среднее значение, дисперсия и стандартное отклонение позволяют увидеть, где находится центр данных, и насколько сильно они разбросаны вокруг этого центра. Эти параметры дают общее представление о наборе данных.
Анализ связей: Ищем закономерности во времени
Базовые характеристики – это хорошо, но они не рассказывают нам о том, как данные связаны между собой во времени. Для этого мы используем другие методы анализа – автокорреляцию и частичную автокорреляцию.
Представьте, что мы хотим узнать, насколько сильно значение в нашем временном ряду зависит от предыдущих значений. Например, зависит ли значение сегодня от значения вчера? Или от значения неделю назад? Автокорреляция показывает эту зависимость. Она измеряется для разных “лагов” – временных сдвигов. Лаг 1 показывает связь между текущим значением и предыдущим, лаг 2 – между текущим значением и значением два периода назад, и так далее. Значение автокорреляции может быть от -1 до 1. Положительное значение говорит о прямой зависимости (чем больше значение в прошлом, тем больше значение в настоящем), отрицательное – об обратной зависимости (чем больше значение в прошлом, тем меньше значение в настоящем), а значение близкое к нулю – об отсутствии зависимости.
В нашем примере, автокорреляции оказались довольно небольшими:
- Лаг 1: -0.036
- Лаг 2: 0.084
- …
- Лаг 10: -0.246
Это говорит о том, что явной линейной зависимости между значениями в разные моменты времени нет. Значение сегодня практически не зависит от того, каким оно было вчера или неделю назад.
Теперь представим, что мы хотим узнать, насколько сильно значение сегодня связано со значением два дня назад, исключив влияние значения вчера. То есть, мы хотим узнать “чистую” связь между этими двумя значениями, без учета промежуточного. Частичная автокорреляция показывает эту “чистую” связь.
К сожалению, из-за технических ограничений в программе, мы смогли корректно рассчитать частичные автокорреляции только для первых трех лагов:
- Лаг 1: -0.036
- Лаг 2: 0.083
- Лаг 3: 0.125
- Остальные лаги равны 0.
Что мы можем сказать о нашем временном ряде?
На основе проведенного анализа можно сделать следующие предварительные выводы:
- Слабая предсказуемость: Значения автокорреляций и частичных автокорреляций невелики. Это говорит о том, что в нашем временном ряду нет ярко выраженных линейных зависимостей. Предсказать будущие значения на основе прошлых довольно сложно.
- Случайный процесс: Вполне возможно, что наш временной ряд представляет собой случайный процесс – последовательность чисел, сгенерированных случайным образом. В таком случае, дальнейший анализ не имеет смысла, так как в данных нет никаких закономерностей.
- Необходимость более сложных методов: Однако, нельзя исключать возможность, что в данных существуют более сложные, нелинейные зависимости, которые не выявляются с помощью автокорреляций. В этом случае необходимо использовать более сложные методы анализа.
Вклад Джорджа Бокса и модели ARIMA
Стоит отметить, что для более глубокого анализа временных рядов часто используются модели, разработанные в рамках подхода, предложенного известным статистиком Джорджем Боксом. Он совместно с Гвендолином Дженкинсом разработал методологию Box-Jenkins, которая привела к созданию моделей ARIMA (Autoregressive Integrated Moving Average). Эти модели позволяют учитывать различные типы зависимостей во временных рядах, включая авторегрессию (зависимость от предыдущих значений), интегрирование (учет трендов) и скользящее среднее (учет случайных колебаний).
Дальнейшие шаги: Куда двигаться дальше
Анализ, проведенный в данной работе, является лишь первым шагом на пути к пониманию временного ряда. Для получения более точных выводов необходимо:
Проверить временной ряд на стационарность. Это означает, что его статистические характеристики (среднее, дисперсия) не должны меняться со временем. Если ряд нестационарен, его необходимо преобразовать (например, взять разности), чтобы привести к стационарному виду.
Построить графики ACF и PACF. Визуальный анализ поможет выявить скрытые закономерности, которые не видны при простом расчете чисел.
Использовать более сложные методы анализа, такие как спектральный анализ, вейвлет-анализ, нейронные сети и другие.
Заключение: Важность анализа временных рядов
В этой работе мы рассмотрели основные методы анализа временного ряда на простом примере. Мы узнали, что такое среднее значение, дисперсия, автокорреляция и частичная автокорреляция. Мы также поняли, как эти показатели могут помочь в понимании структуры данных и выявлении закономерностей.
Несмотря на то, что наш временной ряд оказался довольно простым и не содержал ярко выраженных закономерностей, полученные знания могут быть полезными для анализа реальных данных. Анализ временных рядов – это мощный инструмент, который позволяет принимать обоснованные решения в различных областях: от экономики и финансов до медицины и экологии.
Помните, что анализ данных – это всегда итеративный процесс. Начинайте с простого, постепенно переходя к более сложному. Используйте различные методы и инструменты, не бойтесь экспериментировать и задавать вопросы. И тогда вы сможете увидеть за цифрами истории, которые скрыты от невооруженного взгляда.
Анализ временного ряда: От цифр к пониманию, от простого к сложному
В предыдущей части нашей работы мы провели анализ временного ряда, используя инструмент, созданный в среде разработки 1С. Мы рассмотрели базовые статистические характеристики, такие как среднее значение, дисперсия и стандартное отклонение. Мы также исследовали автокорреляции и частичные автокорреляции, стремясь выявить скрытые взаимосвязи между значениями во временном ряду. Хотя наш пример был упрощенным и показал лишь начальные этапы анализа, он позволил нам окунуться в мир данных и понять основные принципы, лежащие в основе анализа временных рядов. Но, как мы помним, анализ, который мы провели, был лишь первым шагом. Существует множество инструментов и методов, которые позволяют глубже погрузиться в эту область. Одним из таких инструментов, внесшим огромный вклад в развитие анализа временных рядов, является подход Бокса-Дженкинса, созданный выдающимся статистиком Джорджем Боксом.
Джордж Бокс и его вклад в анализ временных рядов
Джордж Бокс, – выдающийся статистик, чье имя навсегда вписано в историю науки о данных. Его вклад в развитие анализа временных рядов трудно переоценить. Он является соавтором подхода Бокса-Дженкинса, который совершил революцию в области обработки данных о процессах, развивающихся во времени.
Бокс родился в 1919 году в Англии. Он получил образование в области математики и статистики, а затем посвятил свою жизнь исследованиям и преподаванию. Его работы охватывают широкий спектр статистических методов, но именно вклад в анализ временных рядов принес ему мировую известность.
Вместе с Гвендолином Дженкинсом Бокс разработал мощную методологию, которая дала ученым и специалистам практичный и последовательный способ анализа и моделирования временных рядов. Этот подход, известный как методология Box-Jenkins, привел к созданию моделей ARIMA (Autoregressive Integrated Moving Average). Модели ARIMA стали одним из наиболее широко используемых инструментов для анализа и прогнозирования временных рядов в различных областях.
Что такое ARIMA?
Представьте себе сложный механизм, который позволяет “видеть” скрытые закономерности во временных рядах и даже предсказывать будущее. Модели ARIMA – это и есть такой механизм, воплощенный в математических формулах. Они учитывают различные типы зависимостей, характерные для данных, изменяющихся во времени.
В основе моделей ARIMA лежат три основных компонента. Первый – авторегрессия (AR), этот компонент учитывает зависимость текущего значения от предыдущих значений временного ряда. Проще говоря, он показывает, как значения ряда “влияют” друг на друга во времени. Представьте себе, что вы наблюдаете за ценой акции. Модель авторегрессии учитывает, что цена сегодня может зависеть от цен вчера, позавчера и так далее. Второй – интегрирование (I). Этот компонент отвечает за обработку трендов во временном ряду. Тренды – это долгосрочные изменения в данных, такие как рост или падение. Если данные показывают восходящий тренд (значения увеличиваются со временем), интегрирование помогает “убрать” этот тренд и сделать ряд более “стационарным”. Стационарный ряд – это ряд, у которого статистические характеристики (например, среднее значение и дисперсия) не меняются со временем. Именно стационарные ряды легче анализировать и прогнозировать. Третий – скользящее среднее (MA). Этот компонент учитывает влияние случайных колебаний, которые могут влиять на значения временного ряда. Случайные колебания – это “шум”, который мешает увидеть основные закономерности. Модель скользящего среднего помогает сгладить эти колебания и выделить основные тренды.
Сочетание этих трех компонентов позволяет моделям ARIMA учитывать широкий спектр зависимостей, характерных для временных рядов. Например, модель ARIMA может учитывать как влияние предыдущих значений (авторегрессия), так и наличие тренда (интегрирование), и случайные колебания (скользящее среднее).
Преимущества и применение моделей ARIMA
Подход Бокса-Дженкинса и модели ARIMA получили широкое распространение благодаря своим преимуществам. Они отличаются гибкостью, позволяя моделировать широкий спектр временных рядов, от простых до очень сложных. Они характеризуются систематичностью, ведь подход Бокса-Дженкинса предоставляет четкую методологию анализа и моделирования, которая включает в себя идентификацию модели, оценку параметров и диагностику. И наконец, они обеспечивают прогнозирование, позволяя делать прогнозы будущих значений временного ряда, что делает их полезными для принятия решений в различных областях.
Модели ARIMA находят применение в самых разных областях. В экономике они используются для прогнозирования экономических показателей, таких как инфляция, ВВП, безработица. В финансах – для анализа и прогнозирования цен на акции, курсов валют, процентных ставок. В метеорологии – для прогнозирования погоды, анализа климатических изменений. В маркетинге – для анализа продаж, планирования рекламных кампаний. В инженерии – для анализа производственных процессов, прогнозирования поломок оборудования.
Методология Box-Jenkins: Путь к пониманию
Подход Бокса-Дженкинса – это не просто набор формул, это целый методологический процесс, который включает в себя несколько этапов. Сначала происходит идентификация модели, в рамках которой проводится анализ данных, построение графиков, расчет автокорреляций (ACF) и частичных автокорреляций (PACF). Эти инструменты помогают определить структуру временного ряда и выбрать подходящую модель ARIMA (то есть, определить значения p, d и q). Затем проводится оценка параметров. На этом этапе происходит оценка параметров выбранной модели с использованием специальных статистических методов. После этого происходит диагностика модели. На данном этапе проверяется адекватность модели, то есть, насколько хорошо она описывает данные. Если модель не описывает данные достаточно хорошо, процесс повторяется (возврат к этапу идентификации). И наконец, последний этап - прогнозирование. Здесь происходит использование построенной модели для прогнозирования будущих значений временного ряда.
Методология Box-Jenkins позволяет аналитику получить полную картину временного ряда.
Заключение: Наследие Джорджа Бокса
Джордж Бокс и его работа оказали огромное влияние на развитие науки о данных. Его подход позволил специалистам получить новые инструменты для анализа и прогнозирования временных рядов, которые нашли применение в самых разных областях. Его подход к анализу временных рядов, основанный на моделях ARIMA, стал стандартным инструментом для специалистов в области экономики, финансов, метеорологии и многих других областях.
Работа Джорджа Бокса – это пример того, как глубокое понимание математики и статистики может привести к созданию инструментов, которые меняют мир. Его наследие продолжает жить в работах ученых и специалистов по всему миру, которые используют модели ARIMA для анализа и прогнозирования временных рядов, делая нашу жизнь более предсказуемой и управляемой. Изучение работ Джорджа Бокса и его современников является важным шагом для тех, кто стремится овладеть искусством анализа данных.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.20.85
Вступайте в нашу телеграмм-группу Инфостарт