Представьте себя эконометрическим детективом, которому поручено раскрыть сложное дело. На столе перед вами лежат не реальные улики, а искусно созданные синтетические данные. Это как если бы вам дали набор улик из детективного романа, а не с места реального преступления. Каждая цифра – это свидетель, дающий показания, но свидетельства эти – плод воображения алгоритма. Ваша задача – понять, что они означают и как складываются в общую картину, осознавая, что имеете дело с моделью, а не с отражением реального мира. Помните, что, как говорил Такеши Амемия, признанный специалист по моделям с ограниченной зависимой переменной, “Эконометрика – это не просто набор инструментов, это искусство понимания данных и построения моделей, способных раскрыть их суть”. Вооружившись этим принципом, и помня об искусственной природе наших данных, приступим к расследованию.
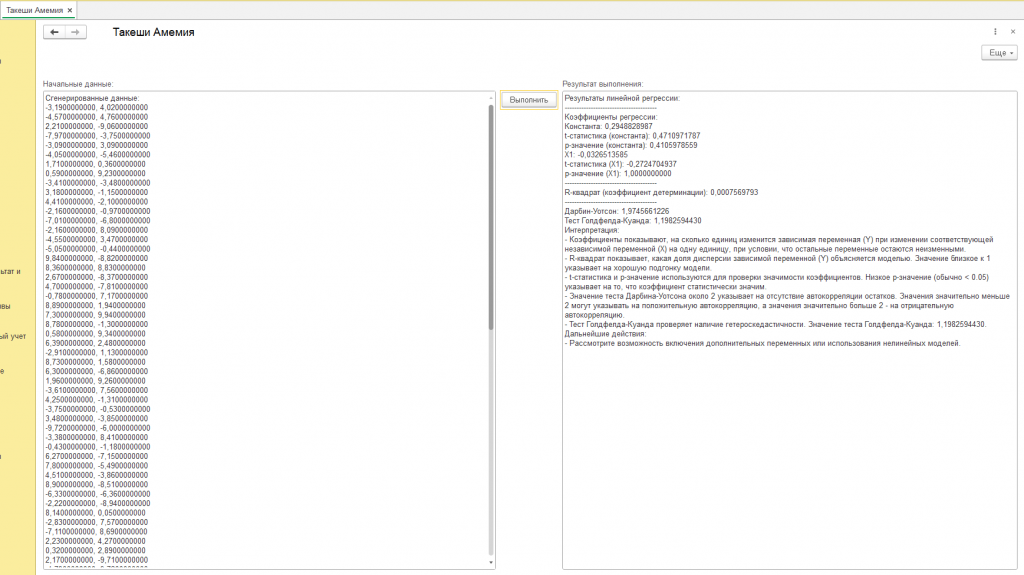
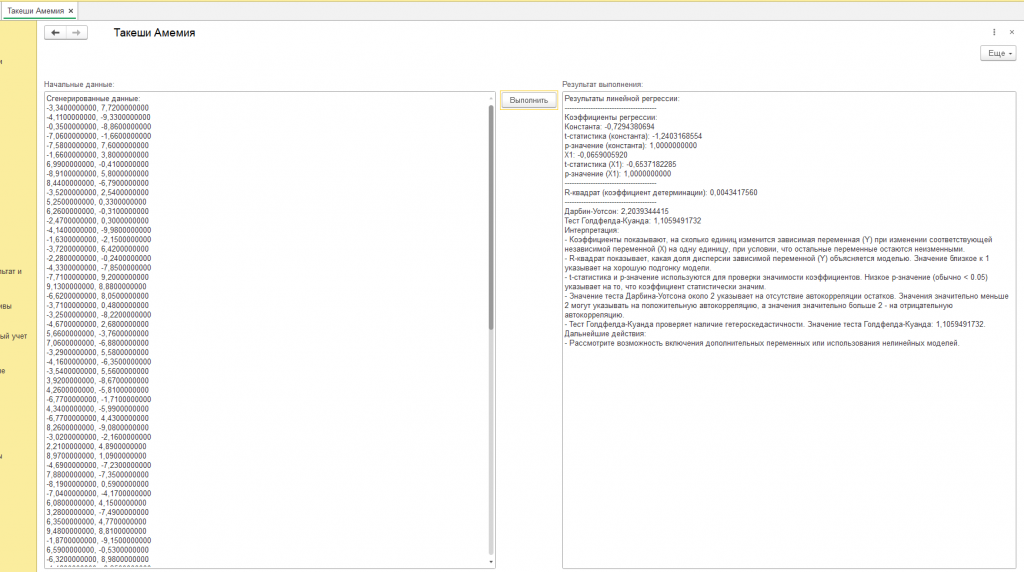
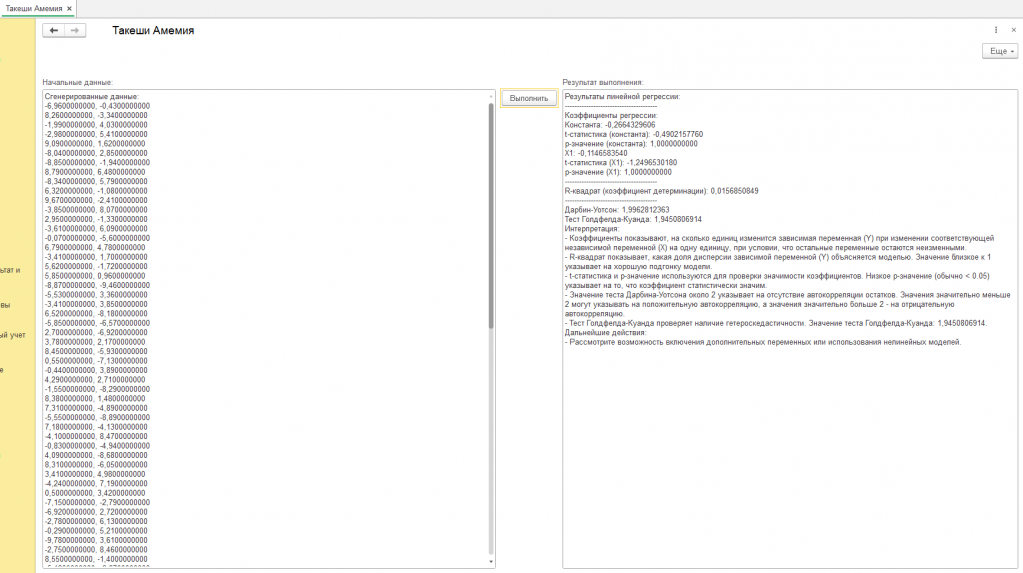
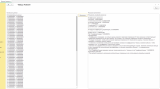
Первым делом внимательно изучим “коэффициенты регрессии” (см. скриншот обработки с подписью "пример") – это словно ориентиры на месте преступления, но нарисованные на карте. “Константа”, равная 0,1967, – это отправная точка, возможно, место, где все началось, но в сгенерированном мире, а не в реальности. Насколько надежна эта отправная точка? Здесь нам на помощь приходят “t-статистика” (0,3345) и “p-значение” (0,4617), оценивающие значимость нашей константы. Они сообщают, что константа статистически незначима. В контексте синтетических данных это скорее говорит о том, что алгоритм, сгенерировавший данные, не запрограммировал значимую роль для константы. Представьте, что мы ищем отпечатки пальцев на месте преступления, но они оставлены не преступником, а художником, рисующим картину.
Далее обратим внимание на “X1” с коэффициентом -0,0777. Это, возможно, ключевая фигура в нашем искусственном деле, оказывающая влияние на ход событий. Отрицательный знак говорит о том, что с увеличением “X1”, зависимая переменная “уменьшается” в нашем смоделированном мире. Но снова встает вопрос о значимости. “T-статистика” (-0,8207) и “p-значение” (1,0000) сообщают, что и этот свидетель дает ненадежные показания. Связь между “X1” и зависимой переменной, вероятно, просто случайный артефакт, возникший в процессе генерации данных.
После допроса отдельных свидетелей посмотрим на общую картину преступления в нашем искусственном мире. “R-квадрат”, равный 0,0068, – это “фотография с места преступления”, показывающая, насколько хорошо наша модель описывает сгенерированные данные. К сожалению, фотография получилась очень размытой: только 0,68% изменений в зависимой переменной объясняются “X1”. Это значит, что наша модель плохо улавливает закономерности, заложенные в алгоритме генерации данных, или же этих закономерностей просто не существует.
Чтобы убедиться, что мы не допустили ошибок в процессе расследования, проведем экспертизу. “Тест Дарбина-Уотсона” (2,2478) – это проверка на наличие “автокорреляции остатков”, своеобразных “эхо” в данных, которые могут исказить результаты. В случае синтетических данных, это тест на то, насколько хорошо алгоритм сгенерировал независимые наблюдения. К счастью, “эхо” отсутствует, и наше расследование ведется корректно, но это не отменяет того факта, что данные – искусственные.
Но осталась еще одна проверка – на “гетероскедастичность”, или “непостоянство улик”. “Тест Голдфелда-Куанда” (0,8026) – это анализ на предмет того, не меняются ли свойства улик в разных частях “места преступления”. Результат теста, к сожалению, не дает однозначного ответа, и требует дополнительных исследований, но помните – даже если бы гетероскедастичность была выявлена, это бы говорило лишь об особенностях работы алгоритма генерации данных, а не о реальных закономерностях.
В итоге, как эконометрические детективы, мы должны сделать важный вывод: мы работали с искусственно созданными данными, и все наши результаты отражают лишь особенности алгоритма генерации, а не реальные взаимосвязи. Модель линейной регрессии оказалась плохим “детектором” закономерностей в этом искусственном мире.
Что же делать дальше? Вместо того чтобы продолжать анализировать искусственные данные, нам необходимо переключиться на реальные “улики”. Представьте, что вместо выдуманного преступления, мы беремся за реальное экономическое явление, отраженное в данных 1С. Например, мы можем попытаться понять, как расходы на рекламу (X1) влияют на объем продаж (Y) в конкретной компании. В этом случае, “уликами” станут данные о продажах и рекламных расходах, собранные в 1С за определенный период.
Вместо того чтобы улучшать алгоритм генерации данных, нам необходимо: во-первых, собрать и подготовить реальные данные из 1С, убедившись в их качестве и достоверности. Во-вторых, на основе этих данных построить модель линейной регрессии и провести анализ, интерпретируя результаты в контексте реальной экономической ситуации. В-третьих, если результаты анализа окажутся неудовлетворительными, рассмотреть возможность включения других факторов, использования более сложных моделей или применения других методов анализа, как это было бы сделано при работе с реальными данными. Помните, что в данном случае цель – не понять, как устроен алгоритм, а выявить реальные закономерности, влияющие на бизнес-процессы компании.
Помните, что эконометрика, как и детективная работа, требует критического мышления и понимания ограничений используемых методов. Работая с синтетическими данными, важно помнить, что результаты отражают лишь особенности алгоритма, и не могут быть автоматически перенесены на реальный мир. Как отметил Такеши Амемия, эконометрика – это искусство, и в нашем случае это искусство требует не только умения анализировать данные, но и умения отличать искусственное от реального и делать правильные выводы, опираясь на контекст. Мы не просто используем инструменты, а творим, стремясь к познанию реальных экономических механизмов, словно настоящие эконометрические детективы, раскрывающие тайны бизнеса, опираясь на достоверные данные из 1С.
Итак, мы увидели, как анализ искусственных данных может привести к малозначимым результатам. Но что, если вместо моделирования мы обратимся к реальным экономическим процессам, происходящим, например, в конкретной компании и зафиксированным в системе 1С? В этом случае, нам потребуется не только умение анализировать данные, но и глубокое понимание используемых методов. И здесь на помощь приходит наследие такого выдающегося эконометриста, как Такеши Амемия, чье имя в бескрайних просторах эконометрики звучит как символ новаторства и глубокого понимания.
Он – не просто ученый, а настоящий мастер, виртуозно владеющий искусством моделирования и тестирования гипотез. Его работы, посвященные моделям с ограниченной зависимой переменной и спецификации тестов, оказали огромное влияние на развитие современной эконометрики и стали неотъемлемой частью арсенала каждого исследователя. Чтобы оценить масштаб этого вклада, необходимо погрузиться в мир эконометрических моделей, понять, что представляет собой ограниченная зависимая переменная и как правильно специфицировать тесты, ведь именно в этих областях талант Амемия проявился наиболее ярко.
Эконометрика, как дисциплина, находится на пересечении экономики, математики и статистики. Это сплав, позволяющий преобразовывать абстрактные экономические концепции в конкретные числовые выражения. Задача эконометрики – количественное измерение и анализ экономических связей, проверка экономических теорий и, что немаловажно, прогнозирование будущих экономических событий. Она становится мостом, соединяющим теорию с эмпирическими данными, давая возможность не только увидеть, как экономические силы действуют в реальности, но и предсказывать их поведение в будущем. Эконометрика, таким образом, позволяет перевести абстрактные экономические концепции на язык цифр, что делает возможным их эмпирическую проверку и использование для принятия управленческих решений, будь то на уровне компании или целой страны.
Регрессионный анализ занимает центральное место в эконометрике, являясь одним из наиболее распространенных и мощных инструментов для исследования взаимосвязей между экономическими переменными. Он позволяет установить зависимость между одной зависимой переменной и одной или несколькими независимыми переменными. Зависимая переменная – это та переменная, которую мы стремимся объяснить или предсказать, она является объектом нашего интереса. Независимые переменные, в свою очередь, рассматриваются как факторы, оказывающие влияние на зависимую переменную, как причины, приводящие к определенным следствиям. Примером может служить исследование влияния уровня образования и опыта работы на заработную плату, где заработная плата выступает в качестве зависимой переменной, а уровень образования и опыт – в качестве независимых.
В основе регрессионного анализа лежит построение математической модели, которая описывает зависимость между переменными. Наиболее простой и распространенной моделью является линейная регрессия, в которой зависимость представляется в виде линейного уравнения. Это уравнение позволяет оценить, на сколько единиц изменится зависимая переменная при изменении независимой переменной на одну единицу, при условии, что остальные факторы остаются неизменными. Однако, реальный мир экономики редко укладывается в простые линейные рамки, и на практике часто встречаются ситуации, когда линейная модель оказывается недостаточно адекватной для описания данных. В таких случаях возникает необходимость в использовании более сложных, нелинейных моделей, способных более точно отразить существующие взаимосвязи.
Методы анализа временных рядов открывают возможности для исследования данных, собранных в последовательные моменты времени. Временной ряд – это, по сути, летопись изменений какой-либо переменной, расположенных в хронологическом порядке. Это может быть ежемесячная статистика продаж компании, ежегодные данные о валовом внутреннем продукте (ВВП) страны или даже ежедневные колебания курса акций на фондовом рынке. Анализ временных рядов становится ценным инструментом для выявления закономерностей и трендов, скрытых в динамике данных.
Анализ временных рядов позволяет выявлять закономерности и тренды в данных, прогнозировать будущие значения переменной и оценивать влияние различных факторов на ее динамику. Разнообразие методов, используемых в анализе временных рядов, позволяет адаптироваться к различным типам данных и исследовательским задачам. Среди наиболее популярных методов можно выделить модели авторегрессии (AR), модели скользящего среднего (MA), модели авторегрессии и скользящего среднего (ARMA) и модели интегрированной авторегрессии и скользящего среднего (ARIMA). Каждая из этих моделей обладает своими особенностями и применяется в зависимости от характеристик временного ряда и целей анализа.
Моделирование одновременных уравнений становится необходимым инструментом, когда речь заходит об анализе систем взаимосвязанных экономических переменных. В реальной экономике сложно найти явления, существующие в изоляции, большинство переменных оказывают взаимное влияние друг на друга, образуя сложные системы обратных связей. Примером такой системы может служить рынок, где спрос и предложение определяются одновременно и оказывают непосредственное воздействие друг на друга. Игнорирование этой взаимосвязи может привести к искаженным результатам и неверным выводам.
Моделирование одновременных уравнений позволяет учитывать обратные связи между переменными и получать более точные оценки их влияния друг на друга. Создание и анализ таких моделей требует использования специальных методов, разработанных именно для этих целей, таких как метод двухшаговых наименьших квадратов (2SLS) и метод трехшаговых наименьших квадратов (3SLS). Эти методы позволяют учесть эндогенность переменных, то есть тот факт, что они одновременно определяются внутри модели, и получить более надежные оценки их параметров.
Статистические тесты играют решающую роль в эконометрике, позволяя исследователям оценивать надежность полученных результатов и делать обоснованные выводы на основе данных. Статистический тест – это, по сути, процедура, с помощью которой можно принять или отвергнуть определенную гипотезу, используя имеющиеся данные. Например, можно использовать статистический тест для проверки гипотезы о том, что уровень образования положительно влияет на заработную плату, или что увеличение рекламных расходов приводит к росту продаж.
Для проведения статистических тестов необходимо четко сформулировать нулевую и альтернативную гипотезы. Нулевая гипотеза – это утверждение, которое мы хотим опровергнуть, это отправная точка, которую мы подвергаем сомнению. Альтернативная гипотеза, напротив, представляет собой утверждение, которое мы принимаем в случае, если нам удается опровергнуть нулевую гипотезу. Например, если мы хотим проверить влияние образования на заработную плату, нулевой гипотезой может быть утверждение об отсутствии влияния образования, а альтернативной – утверждение о наличии положительного влияния.
После формулировки гипотез необходимо выбрать статистику теста, которая позволит оценить, насколько данные соответствуют нулевой гипотезе. Статистика теста – это числовая величина, рассчитываемая на основе данных и позволяющая оценить степень отклонения наблюдаемых результатов от тех, которые ожидались бы при верности нулевой гипотезы. Затем, на основе распределения статистики теста, определяется p-значение, которое показывает вероятность получения наблюдаемых данных при условии, что нулевая гипотеза верна. P-значение, таким образом, является мерой доказательности против нулевой гипотезы. Если p-значение оказывается меньше заранее заданного уровня значимости (обычно 0,05 или 0,01), то мы отвергаем нулевую гипотезу и принимаем альтернативную, считая, что данные предоставляют достаточно свидетельств в пользу альтернативной гипотезы.
Ограниченные зависимые переменные стали одной из ключевых областей исследований Такеши Амемия, открыв новые горизонты в эконометрическом моделировании. Ограниченная зависимая переменная – это переменная, значения которой ограничены определенным диапазоном или удовлетворяют определенным условиям. Это означает, что обычные методы регрессионного анализа, разработанные для непрерывных переменных, могут оказаться неадекватными и привести к искаженным результатам. Примерами ограниченных зависимых переменных служат бинарные переменные, принимающие только два значения (0 или 1), цензурированные переменные, значения которых наблюдаются только в определенном диапазоне, усеченные переменные, значения которых наблюдаются только для определенной подгруппы наблюдений, и категориальные переменные, принимающие несколько дискретных значений.
Использование стандартных методов регрессионного анализа для моделей с ограниченной зависимой переменной может привести к смещенным и несостоятельным оценкам. Это связано с тем, что предположения, лежащие в основе этих методов, не выполняются для ограниченных переменных. Поэтому для анализа таких моделей необходимо использовать специальные методы, учитывающие ограничения на значения зависимой переменной.
Для анализа бинарных переменных широко используются модели логистической регрессии (logit) и пробит-регрессии (probit). Эти модели позволяют оценить вероятность того, что зависимая переменная примет значение 1, в зависимости от значений независимых переменных. В отличие от линейной регрессии, модели logit и probit используют нелинейные функции для связи между независимыми и зависимой переменными, что позволяет корректно моделировать вероятность, которая всегда должна находиться в диапазоне от 0 до 1. Модели logit и probit основаны на использовании логистической и нормальной функций распределения, соответственно, что определяет их математические свойства и особенности применения.
Для анализа цензурированных и усеченных переменных разработаны модели Тобина (Tobit models), названные в честь нобелевского лауреата Джеймса Тобина. Эти модели позволяют учитывать тот факт, что значения зависимой переменной наблюдаются только в определенном диапазоне, и получать состоятельные оценки параметров модели. Модели Тобина нашли широкое применение в различных областях экономики, от анализа потребительского спроса до исследований рынка труда.
Для анализа категориальных переменных используются модели мультиномиальной логистической регрессии (multinomial logit) и упорядоченной логистической регрессии (ordered logit). Модели multinomial logit позволяют оценить вероятность того, что зависимая переменная примет каждое из возможных значений, что особенно полезно при анализе выбора из нескольких альтернатив. Модели ordered logit, в свою очередь, используются для анализа категориальных переменных, значения которых имеют определенный порядок, например, уровень образования или степень удовлетворенности.
Спецификационные тесты стали еще одной важной областью исследований Такеши Амемия, внесшей значительный вклад в повышение надежности и достоверности эконометрического анализа. Спецификационный тест – это, по сути, инструмент для проверки правильности построенной эконометрической модели. Правильная спецификация означает, что модель адекватно отражает зависимость между переменными и удовлетворяет всем необходимым предположениям, лежащим в ее основе.
Использование неправильно специфицированной модели может привести к серьезным последствиям, включая смещенные и несостоятельные оценки, а также неверные выводы и прогнозы. Поэтому спецификационные тесты играют критически важную роль в эконометрическом анализе, позволяя выявить недостатки модели и улучшить ее спецификацию. Они служат своеобразным фильтром, отсеивающим неадекватные модели и гарантирующим надежность полученных результатов.
Существует большое разнообразие спецификационных тестов, каждый из которых предназначен для проверки определенного аспекта модели. Выбор конкретного теста зависит от типа модели, характера данных и исследовательских задач. Среди наиболее распространенных спецификационных тестов можно выделить тесты на гетероскедастичность, тесты на автокорреляцию, тесты на нормальность, тесты на пропущенные переменные и тесты на эндогенность.
Тесты на гетероскедастичность позволяют проверить предположение о постоянстве дисперсии остатков. Если дисперсия остатков не является постоянной, то оценки параметров модели могут быть неэффективными, и необходимо использовать специальные методы для получения состоятельных оценок. Тесты на автокорреляцию, в свою очередь, позволяют проверить предположение об отсутствии корреляции между остатками в разные моменты времени. Наличие автокорреляции может указывать на неправильную спецификацию модели или на необходимость использования моделей временных рядов.
Тесты на нормальность позволяют проверить предположение о нормальном распределении остатков. Хотя многие методы эконометрики являются асимптотически нормальными, то есть становятся точными при больших объемах выборки, отклонение от нормальности может негативно сказаться на точности результатов при малых и средних выборках. Тесты на пропущенные переменные позволяют проверить, не упустили ли мы какие-либо важные факторы, которые могут влиять на зависимую переменную. Пропуск важных переменных может привести к смещению оценок параметров и искажению результатов анализа.
Тесты на эндогенность позволяют проверить, не являются ли какие-либо из независимых переменных эндогенными, то есть зависящими от зависимой переменной. Эндогенность может возникнуть, если между переменными существует обратная связь, или если на обе переменные влияет какой-либо неучтенный фактор. Наличие эндогенности может привести к серьезным смещениям в оценках параметров, и необходимо использовать специальные методы, такие как метод инструментальных переменных, для получения состоятельных оценок.
Такеши Амемия внес неоценимый вклад в разработку и анализ многих из этих спецификационных тестов. Его работы позволили эконометристам лучше понимать свойства и ограничения различных тестов и правильно использовать их для проверки своих моделей. Он, по сути, создал “инструментарий” для оценки адекватности эконометрических моделей, которым активно пользуются исследователи по всему миру.
Подводя итог, можно с уверенностью сказать, что Такеши Амемия – это выдающийся ученый, чьи труды оказали огромное влияние на развитие современной эконометрики. Его вклад в моделирование ограниченных зависимых переменных и разработку спецификационных тестов стал классическим и продолжает вдохновлять исследователей по всему миру. Его талант, знания и преданность науке служат примером для всех, кто занимается эконометрическими исследованиями и стремится к познанию сложных экономических явлений. Работы Такеши Амемия позволяют исследователям более точно моделировать экономические процессы, правильно интерпретировать результаты анализа и принимать обоснованные решения, опираясь на надежные эмпирические данные. Его наследие продолжает жить и направлять эконометристов на поиск новых знаний и решений сложных экономических проблем. Его имя навсегда вписано в историю эконометрики, как символ новаторства, глубокого понимания и стремления к истине.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.20.85
Вступайте в нашу телеграмм-группу Инфостарт