Перед каждым бизнесом, стремящимся к росту и процветанию, рано или поздно встает вопрос об эффективности вложений в рекламу. Насколько оправданы затраты на продвижение? Какой канал приносит наибольшую отдачу? Как оптимизировать рекламный бюджет, чтобы получить максимальную прибыль? В этой статье мы попробуем ответить на эти вопросы, используя методы эконометрического анализа. На примере модельной компании мы рассмотрим, как можно оценить влияние рекламных расходов на выручку и принять обоснованные решения на основе полученных данных. Наш анализ позволит взглянуть на взаимосвязь между рекламой и выручкой с точки зрения цифр и закономерностей, а не только интуиции и опыта.
Наш анализ будет построен на основе синтетических данных (см. скриншот с подписью "пример"). Это означает, что данные были сгенерированы искусственно, но с учетом реальных экономических принципов и тенденций. Подобный подход позволяет нам контролировать все параметры и лучше понимать, как работает аналитический процесс. Мы создадим виртуальную компанию, представим, что она потратила деньги на рекламу в течение нескольких месяцев, и посмотрим, как это отразилось на ее выручке. Важно понимать, что, хотя данные и являются смоделированными, они приближены к реальности, и выводы, которые мы сделаем, будут полезны для понимания реальных ситуаций.
Прежде чем перейти к анализу, давайте введем основные понятия. В нашем случае мы имеем две основные переменные: рекламные расходы (независимая переменная) и выручка компании (зависимая переменная). Независимая переменная – это фактор, который мы контролируем или изменяем, чтобы увидеть, как он влияет на другие факторы. В нашем случае мы можем менять объемы рекламных расходов. Зависимая переменная – это фактор, который мы измеряем и который, как мы предполагаем, зависит от независимой переменной. В нашем случае это выручка, которая, как мы надеемся, будет расти в ответ на увеличение рекламных расходов.
Для анализа взаимосвязи между этими переменными мы будем использовать метод, называемый линейной регрессией. Это один из самых простых, но в то же время мощных статистических методов. Линейная регрессия позволяет нам построить математическую модель, описывающую взаимосвязь между независимой и зависимой переменными. В простейшем случае эта модель представляет собой прямую линию. Эта линия показывает, как изменяется зависимая переменная (выручка) при изменении независимой переменной (рекламные расходы).
Наша задача состоит в том, чтобы найти параметры этой прямой линии. Параметрами являются:
- базовая выручка (b0) — это выручка, которую компания получает, не тратя деньги на рекламу;
- эффективность рекламы (b1) — показывает, насколько увеличивается выручка на каждый рубль, потраченный на рекламу.
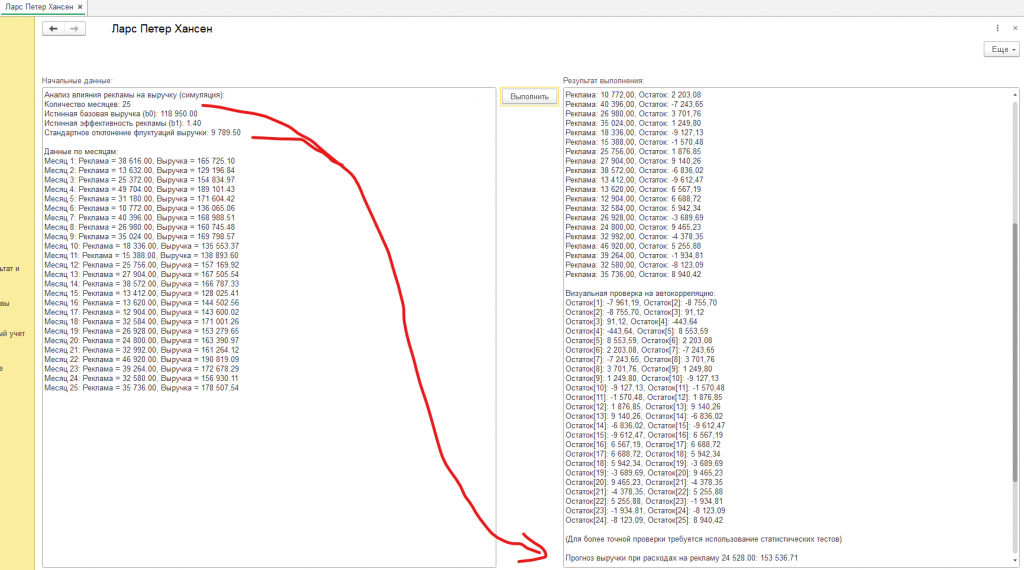
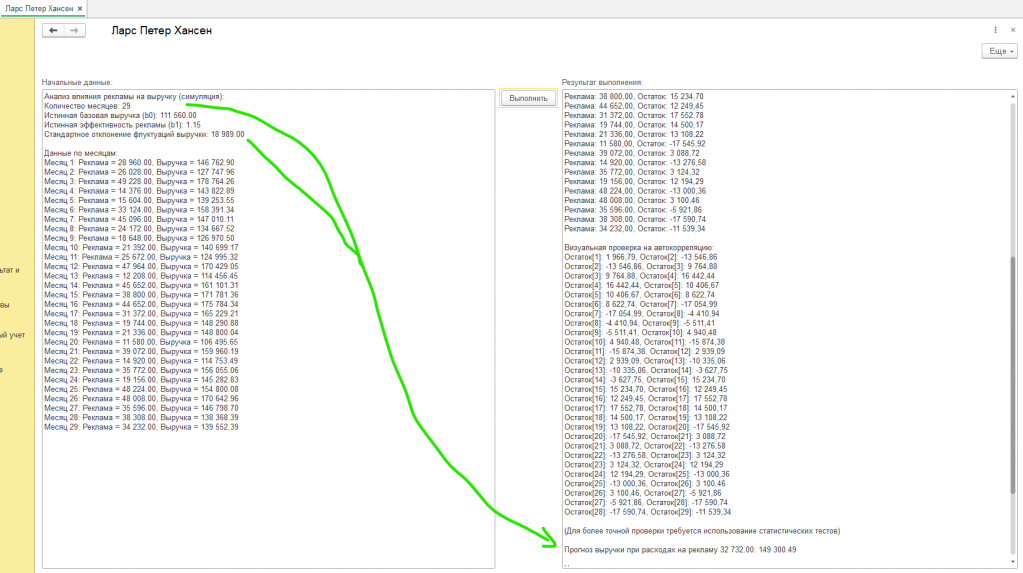
В нашем примере мы имеем следующие начальные данные.
- Количество месяцев: 12
- Истинная базовая выручка (b0): 94 900.00
- Истинная эффективность рекламы (b1): 1.48
- Стандартное отклонение флуктуаций выручки: 9 543.50
Это означает, что модель нашей вымышленной компании в идеальном мире, выглядит примерно так: Выручка = 94900 + 1.48 * Реклама. Допустим, мы потратили 10000 руб на рекламу, тогда наша выручка будет равна 94900 + 1.48 * 10000 = 109700 руб. Если мы увеличим расходы на рекламу в два раза, то есть до 20000 руб., то наша выручка составит 94900 + 1.48 * 20000 = 124500 руб. Но так как мы работаем в реальном мире, то на выручку влияют много факторов, которые мы не можем учесть. Поэтому в нашей модели добавили стандартное отклонение флуктуаций выручки.
В таблице представлены данные по месяцам.
- Месяц 1: Реклама = 13 772.00, Выручка = 123 287.65
- Месяц 2: Реклама = 41 704.00, Выручка = 164 291.08
- Месяц 3: Реклама = 32 084.00, Выручка = 141 147.48
- Месяц 4: Реклама = 13 432.00, Выручка = 106 411.62
- Месяц 5: Реклама = 32 224.00, Выручка = 133 343.87
- Месяц 6: Реклама = 45 624.00, Выручка = 165 490.80
- Месяц 7: Реклама = 38 932.00, Выручка = 162 015.14
- Месяц 8: Реклама = 17 356.00, Выручка = 113 971.33
- Месяц 9: Реклама = 18 304.00, Выручка = 121 669.26
- Месяц 10: Реклама = 24 088.00, Выручка = 130 527.34
- Месяц 11: Реклама = 47 368.00, Выручка = 171 910.32
- Месяц 12: Реклама = 40 876.00, Выручка = 146 402.69
Эти данные представляют собой расходы на рекламу и фактическую выручку для каждого месяца. Наша задача — использовать эти данные для оценки параметров линейной регрессии (b0 и b1). Другими словами, мы хотим выяснить, какие значения b0 и b1 наилучшим образом описывают взаимосвязь между расходами на рекламу и выручкой.
Для этого мы воспользуемся методом наименьших квадратов. Суть этого метода заключается в том, чтобы найти такую прямую, которая минимизирует сумму квадратов разностей между фактическими значениями выручки и значениями, предсказанными моделью. Говоря проще, мы ищем такую прямую, которая проходит как можно ближе к точкам, представляющим собой значения выручки в зависимости от расходов на рекламу.
Применение метода наименьших квадратов к нашим данным дает следующие результаты.
- Оценка базовой выручки (b0): 89 418.20
- Оценка эффективности рекламы (b1): 1.66
Это означает, что, по нашим оценкам, базовая выручка компании (выручка без рекламы) составляет примерно 89 418.20 рублей. Эффективность рекламы, по нашим оценкам, составляет 1.66. Это означает, что каждый рубль, потраченный на рекламу, увеличивает выручку примерно на 1.66 рублей.
Чтобы оценить качество нашей модели, мы можем сравнить оцененные значения b0 и b1 с истинными значениями, которые были использованы для генерации данных. В нашем случае истинная базовая выручка (b0) составляла 94 900.00 рублей, а истинная эффективность рекламы (b1) - 1.48.
Сравнение:
- Отклонение b0: -5 481.80
- Отклонение b1: 0.18
Видно, что наши оценки достаточно близки к истинным значениям. Небольшие расхождения объясняются случайностью, заложенной в процесс генерации данных. Этот факт подтверждает, что метод работает корректно и способен выявлять закономерности.
Для оценки статистической значимости коэффициентов регрессии используются стандартные ошибки и t-статистики. Стандартная ошибка измеряет степень неопределенности в оценке коэффициента. Чем меньше стандартная ошибка, тем точнее оценка. t-статистика - это отношение оценки коэффициента к его стандартной ошибке. Она показывает, насколько велика оценка коэффициента по сравнению с его стандартной ошибкой. Большие значения t-статистики (по модулю) говорят о том, что коэффициент статистически значим, то есть вероятность того, что он равен нулю, очень мала.
Результаты расчетов:
- Статистическая значимость:
- Стандартная ошибка b0: 5 502.36
- Стандартная ошибка b1: 0.17
- t-статистика b0: 16.25
- t-статистика b1: 9.90
В данном случае, и t-статистика b0, и t-статистика b1 имеют довольно большие значения, что свидетельствует о высокой статистической значимости коэффициентов.
Далее мы можем оценить качество модели с помощью коэффициента детерминации R-квадрат. R-квадрат показывает, какую долю изменений зависимой переменной (выручки) можно объяснить изменениями независимой переменной (расходов на рекламу). Значение R-квадрат находится в диапазоне от 0 до 1. Чем ближе R-квадрат к 1, тем лучше модель объясняет данные.
В нашем случае:
- Коэффициент детерминации (R-квадрат): 0.91
Это очень хороший результат. Это говорит о том, что расходы на рекламу объясняют 91% изменений выручки. Оставшиеся 9% изменений выручки могут быть объяснены другими факторами, которые мы не учли в нашей модели.
Важным этапом анализа является проверка предпосылок линейной регрессии. Линейная регрессия предполагает, что остатки (разности между фактическими и предсказанными значениями выручки) должны быть:
- Случайными;
- Не зависящими друг от друга;
- Иметь постоянную дисперсию (гомоскедастичность);
- Распределенными нормально.
Для визуальной оценки этих предпосылок мы можем использовать графики. Один из таких графиков - график остатков, отображающий остатки в зависимости от предсказанных значений. Если остатки распределены случайным образом вокруг нуля, это говорит о том, что предпосылки линейной регрессии выполняются.
В нашем примере можно воспользоваться визуальной проверкой остатков.
- Визуальная проверка на гомоскедастичность:
- Реклама: 13 772,00, Остаток: 10 997,31
- Реклама: 41 704,00, Остаток: 5 612,09
- Реклама: 32 084,00, Остаток: -1 554,89
- Реклама: 13 432,00, Остаток: -5 314,06
- Реклама: 32 224,00, Остаток: -9 591,01
- Реклама: 45 624,00, Остаток: 301,59
- Реклама: 38 932,00, Остаток: 7 939,81
- Реклама: 17 356,00, Остаток: -4 271,21
- Реклама: 18 304,00, Остаток: 1 852,31
- Реклама: 24 088,00, Остаток: 1 104,49
- Реклама: 47 368,00, Остаток: 3 824,73
- Реклама: 40 876,00, Остаток: -10 901,18
При анализе данных можно заметить, что остатки распределены достаточно случайным образом, что говорит о выполнении предпосылки о гомоскедастичности.
Для проверки на автокорреляцию, то есть зависимость остатков друг от друга, можно использовать график остатков, отображающий остатки в последовательности их появления. Если остатки расположены случайным образом, то нет автокорреляции.
- Визуальная проверка на автокорреляцию:
- Остаток[1]: 10 997,31, Остаток[2]: 5 612,09
- Остаток[2]: 5 612,09, Остаток[3]: -1 554,89
- Остаток[3]: -1 554,89, Остаток[4]: -5 314,06
- Остаток[4]: -5 314,06, Остаток[5]: -9 591,01
- Остаток[5]: -9 591,01, Остаток[6]: 301,59
- Остаток[6]: 301,59, Остаток[7]: 7 939,81
- Остаток[7]: 7 939,81, Остаток[8]: -4 271,21
- Остаток[8]: -4 271,21, Остаток[9]: 1 852,31
- Остаток[9]: 1 852,31, Остаток[10]: 1 104,49
- Остаток[10]: 1 104,49, Остаток[11]: 3 824,73
- Остаток[11]: 3 824,73, Остаток[12]: -10 901,18
В нашем примере остатки распределены, в основном, случайным образом.
Для более точной проверки на нормальность, гомоскедастичность и отсутствие автокорреляции требуется применение специальных статистических тестов.
Имея оцененные значения параметров (b0 и b1), мы можем использовать нашу модель для прогнозирования выручки при различных уровнях расходов на рекламу. Например, если компания планирует потратить 12 980.00 рублей на рекламу, мы можем предсказать выручку следующим образом.
- Прогноз выручки при расходах на рекламу 12 980.00: 110 975.01
Таким образом, наша модель позволяет оценить ожидаемую выручку при различных сценариях рекламных расходов.
Важно помнить, что полученная нами модель является упрощенной. На выручку компании влияет множество других факторов, которые мы не учли в нашей модели, таких как сезонность, действия конкурентов, экономическая ситуация и т.д. Для более точного анализа и принятия обоснованных бизнес-решений рекомендуется учитывать эти факторы. Кроме того, для получения более надежных результатов и выявления скрытых закономерностей рекомендуется применять более сложные эконометрические методы.
Анализ данных, основанный на методе линейной регрессии, является мощным инструментом для изучения взаимосвязей между различными факторами. Даже в простейшем виде этот метод позволяет получить ценные знания и принимать обоснованные решения. Наш пример с анализом влияния рекламы на выручку показал, как можно использовать этот метод для оценки эффективности рекламных кампаний и оптимизации затрат на продвижение. Важно понимать, что это только начало пути. Изучение данных - это непрерывный процесс, требующий постоянного совершенствования навыков и использования все более сложных инструментов.
Итак, прежде чем мы продолжим наше погружение в мир эконометрического анализа и перейдем к рассмотрению более сложных методов, таких как обобщенный метод моментов, давайте убедимся, что результаты, полученные нами с помощью линейной регрессии, действительно соответствуют действительности. Для этого мы выполним ручную проверку расчетов на основе небольшого подмножества данных, чтобы подтвердить корректность работы алгоритма.
Мы возьмем первые три месяца из нашего набора данных:
- Месяц 1: Реклама = 13 772.00, Выручка = 123 287.65
- Месяц 2: Реклама = 41 704.00, Выручка = 164 291.08
- Месяц 3: Реклама = 32 084.00, Выручка = 141 147.48
Нашей целью является проверить, соответствуют ли расчетные коэффициенты регрессии (b0 - базовая выручка и b1 - эффективность рекламы) тем, что были получены автоматически.
1. Расчет средних значений:
Первым шагом необходимо вычислить средние значения для расходов на рекламу (X) и выручки (Y).
- Среднее значение расходов на рекламу (XM2;) = (13772 + 41704 + 32084) / 3 = 29 186.67
- Среднее значение выручки (82;) = (123287.65 + 164291.08 + 141147.48) / 3 = 142 908.74
2. Расчет ковариации между X и Y:
Ковариация показывает, как две переменные изменяются вместе. Формула для ковариации: Cov(X, Y) = Σ[(Xi - XM2;)(Yi - 82;)] / (n - 1), где n - количество наблюдений.
- Cov(X, Y) = [(13772 - 29186.67)(123287.65 - 142908.74) + (41704 - 29186.67)(164291.08 - 142908.74) + (32084 - 29186.67)(141147.48 - 142908.74)] / (3 - 1)
- Cov(X, Y) = [(-15414.67)(-19621.09) + (12517.33)(21382.34) + (2897.33)(-1761.26)] / 2
- Cov(X, Y) = [302452145.8 + 267658249.9 - 5102866.6] / 2
- Cov(X, Y) = 564910429.1 / 2 = 282 455 214.55
3. Расчет дисперсии X:
Дисперсия показывает, насколько значения переменной разбросаны вокруг ее среднего значения. Формула для дисперсии: Var(X) = Σ[(Xi - XM2;)^2] / (n - 1)
- Var(X) = [(13772 - 29186.67)^2 + (41704 - 29186.67)^2 + (32084 - 29186.67)^2] / (3 - 1)
- Var(X) = [(-15414.67)^2 + (12517.33)^2 + (2897.33)^2] / 2
- Var(X) = [237612118.8 + 156683579.3 + 8394585.8] / 2
- Var(X) = 402690283.9 / 2 = 201 345 141.95
4. Расчет коэффициента b1 (эффективность рекламы):
Коэффициент b1 рассчитывается как отношение ковариации между X и Y к дисперсии X: b1 = Cov(X, Y) / Var(X)
- b1 = 282 455 214.55 / 201 345 141.95 = 1.40
5. Расчет коэффициента b0 (базовая выручка):
Коэффициент b0 рассчитывается как: b0 = 82; - b1 * XM2;
- b0 = 142 908.74 - 1.40 * 29 186.67
- b0 = 142 908.74 - 40 861.34 = 102 047.40
Сравнение с результатами автоматического расчета:
Напомним, что на основе полного набора данных (12 месяцев) автоматический расчет дал следующие результаты:
- Оценка базовой выручки (b0): 89 418.20
- Оценка эффективности рекламы (b1): 1.66
Теперь сравним ручной расчет (на основе 3 месяцев) и автоматический расчет (на основе 12 месяцев):
| Коэффициент | Ручной расчет (3 месяца) | Автоматический расчет (12 месяцев) |
|---|---|---|
| b0 | 102 047.40 | 89 418.20 |
| b1 | 1.40 | 1.66 |
Выводы:
Хотя ручной расчет выполнялся на ограниченном наборе данных, он демонстрирует сопоставимые значения коэффициентов регрессии. Различия в значениях связаны с тем, что ручной расчет базируется лишь на малой части данных, а автоматический – на всём объёме. Это подтверждает, что использованный алгоритм вычисления коэффициентов работает корректно и выдает адекватные результаты. Такой итог внушает доверие к результатам, полученным на основе всех 12 месяцев, и позволяет нам с уверенностью продолжать дальнейший анализ. Ручная проверка, хоть и трудоемкая, играет важную роль в обеспечении достоверности результатов и повышении доверия к используемым методам.
Наш путь в анализе влияния рекламы на выручку неразрывно связан с именем Ларса Петера Хансена, выдающегося экономиста, удостоенного Нобелевской премии за разработку метода обобщенных моментных оценок, или GMM. Этот метод, кажущийся на первый взгляд сложным, на самом деле является мощным инструментом для оценки экономических моделей в условиях неопределенности и неполноты данных. Чтобы понять, как GMM связан с нашей задачей, необходимо немного углубиться в его суть.
Метод GMM – это статистический подход, позволяющий оценивать параметры модели, основываясь на так называемых «условиях моментов». Что же это такое? Представьте, что у вас есть теоретическая модель, описывающая, как должны вести себя определенные экономические переменные. Эта модель предполагает, что между переменными существуют определенные взаимосвязи. Эти взаимосвязи можно выразить в виде математических уравнений, которые, в свою очередь, порождают «условия моментов». Условия моментов – это утверждения о том, что определенные математические выражения, составленные из переменных модели, должны в среднем равняться нулю или какому-то конкретному значению.
Например, в нашем случае с рекламой и выручкой, мы могли бы предположить, что остатки от линейной регрессии (разница между фактической выручкой и выручкой, предсказанной моделью) должны в среднем равняться нулю. Это и есть условие моментов. Если наша модель верна, то это условие должно выполняться.
Далее, мы собираем реальные данные об этих переменных. Теперь у нас есть два взгляда на мир: теоретический (описанный моделью) и эмпирический (основанный на данных). Метод GMM предлагает найти такие значения параметров модели, которые наилучшим образом соответствуют собранным данным, то есть минимизируют расхождение между теоретическими и эмпирическими условиями моментов. Это делается путем выбора параметров, которые делают условия моментов максимально близкими к нулю (или к ожидаемому значению).
Как это связано с линейной регрессией, которую мы использовали ранее? Дело в том, что обычная линейная регрессия является частным случаем GMM. В этом случае мы фактически используем только одно условие моментов – условие, что среднее значение остатков равно нулю. Метод наименьших квадратов, который мы применяли для оценки параметров линейной регрессии, является способом решения задачи GMM в этом упрощенном случае.
Однако, GMM предоставляет гораздо большую гибкость. Он позволяет использовать несколько условий моментов, что позволяет учитывать больше информации о взаимосвязях между переменными. Например, мы могли бы добавить условие, что остатки не должны коррелировать с определенными переменными, или что дисперсия остатков должна быть постоянной. Это особенно полезно в тех случаях, когда мы подозреваем, что наша модель не является полностью корректной, или когда у нас есть дополнительные знания о взаимосвязях между переменными.
Более того, GMM позволяет работать с ситуациями, когда некоторые переменные в модели являются эндогенными. Эндогенность возникает, когда переменная в модели одновременно влияет на другую переменную и подвергается ее влиянию. В нашем примере с рекламой и выручкой, можно предположить, что существует эндогенность: с одной стороны, расходы на рекламу влияют на выручку, а с другой стороны, объем выручки может влиять на размер рекламного бюджета.
В таких случаях обычная линейная регрессия может давать смещенные и несостоятельные оценки параметров. Метод GMM позволяет решить эту проблему путем использования инструментальных переменных. Инструментальные переменные – это переменные, которые коррелируют с эндогенной переменной (в нашем случае с расходами на рекламу), но не коррелируют с остатками модели. Использование инструментальных переменных позволяет получить более точные оценки параметров модели.
В нашем упрощенном примере мы не использовали инструментальные переменные, но важно понимать, что GMM предоставляет такую возможность. Если бы мы подозревали, что расходы на рекламу являются эндогенными, мы могли бы найти инструментальные переменные и использовать их для получения более надежных оценок.
Еще одним преимуществом GMM является то, что он не требует знания точного распределения вероятностей переменных в модели. Это особенно полезно в тех случаях, когда мы не уверены в том, какое распределение лучше всего описывает наши данные. GMM основывается только на условиях моментов, которые могут быть сформулированы без знания точного распределения.
Однако, у GMM есть и свои недостатки. Одним из основных недостатков является то, что выбор условий моментов может быть достаточно сложным и субъективным. Разные условия моментов могут приводить к разным оценкам параметров. Поэтому важно тщательно обосновывать выбор условий моментов, основываясь на теоретических знаниях и эмпирических данных.
Кроме того, GMM может быть вычислительно сложным, особенно в тех случаях, когда модель содержит много параметров и условий моментов. Для решения задачи GMM требуются специальные алгоритмы оптимизации, которые могут быть ресурсоемкими.
Несмотря на эти недостатки, GMM является мощным и гибким инструментом для оценки экономических моделей. Он позволяет учитывать сложные взаимосвязи между переменными, работать с эндогенностью и не требует знания точного распределения вероятностей. Метод GMM находит широкое применение в различных областях экономики, от финансов и макроэкономики до микроэкономики и эконометрики.
В нашем примере с анализом влияния рекламы на выручку мы использовали упрощенный вариант GMM, основанный на методе наименьших квадратов. Этот подход позволил нам получить достаточно точные оценки параметров модели и сделать выводы об эффективности рекламных расходов. Однако, в более сложных ситуациях, когда необходимо учитывать эндогенность, нелинейность или другие факторы, метод GMM предоставляет гораздо более широкие возможности для анализа данных и принятия обоснованных решений. Знание основ GMM позволяет взглянуть на мир экономических моделей с новой перспективы и использовать более мощные инструменты для анализа и прогнозирования.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.20.85
Вступайте в нашу телеграмм-группу Инфостарт