Хэлберт Уайт – выдающийся экономист, внесший значительный вклад в развитие эконометрических методов. Его имя неразрывно связано с разработкой мощного инструмента для анализа регрессионных моделей – теста Уайта на гетероскедастичность. В основе этого теста лежит глубокое понимание предпосылок классической линейной регрессии и последствий нарушения этих предпосылок, в частности, предположения о гомоскедастичности – постоянстве дисперсии случайных ошибок. Нарушение этого предположения, то есть гетероскедастичность, приводит к неэффективным и, зачастую, некорректным оценкам параметров регрессии, снижая точность и надежность результатов анализа. Уайт предложил элегантное и сравнительно простое решение для обнаружения этой проблемы.
Чтобы глубже понять значимость теста Уайта, необходимо четко представлять себе, что такое гетероскедастичность. Говоря простым языком, гетероскедастичность означает, что разброс ошибок в регрессионной модели не является постоянным для всех наблюдений. Представьте себе ситуацию, когда вы пытаетесь предсказать цены на недвижимость. Если ошибка предсказания (разница между фактической ценой и предсказанной моделью) зависит от размера дома (например, для больших домов ошибка может быть больше), то это пример гетероскедастичности. В противоположность этому, гомоскедастичность предполагает, что ошибка предсказания имеет одинаковый разброс для всех наблюдений, независимо от значения объясняющих переменных.
До появления теста Уайта, проверка на гетероскедастичность часто осуществлялась с помощью визуальных методов, основанных на анализе графиков остатков регрессии. Эти методы, хотя и давали определенное представление о наличии или отсутствии гетероскедастичности, были субъективными и не предоставляли возможности для количественной оценки степени нарушения предположения о гомоскедастичности. Более формализованные тесты, существовавшие ранее, также часто были ограничены в своей применимости и требовали сильных предположений о природе гетероскедастичности. Таким образом, потребность в надежном и универсальном тесте была очевидна. Например, проверка графиков остатков против предсказанных значений или объясняющих переменных могла дать предварительное представление, но не предлагала строгого статистического обоснования.
Тест Уайта, разработанный в 1980 году, представил собой значительный шаг вперед. Его значимость заключается в способности обнаруживать гетероскедастичность любой формы, не требуя предварительных предположений о ее виде. Вместо того чтобы предполагать конкретную структуру гетероскедастичности (например, линейную зависимость дисперсии от объясняющих переменных), тест Уайта проверяет гипотезу о гомоскедастичности, используя общую модель, где дисперсия ошибки может быть любой нелинейной функцией объясняющих переменных. Это делает тест Уайта чрезвычайно гибким и применимым к широкому кругу эконометрических задач.
Методология теста Уайта опирается на вспомогательную регрессию. Квадраты остатков исходной регрессионной модели используются в качестве зависимой переменной, а объясняющие переменные исходной модели и их квадраты, а также все возможные их попарные произведения (в случае множественной регрессии) – в качестве объясняющих переменных. Затем, для этой вспомогательной регрессии, вычисляется статистика F-критерия (или, в случае одной объясняющей переменной, статистика хи-квадрат, как было использовано в примере). Высокое значение этой статистики указывает на значимое отклонение от гипотезы о гомоскедастичности, то есть на наличие гетероскедастичности. Для лучшего понимания, рассмотрим упрощенный пример. Предположим, у нас есть простая регрессионная модель: Y = β0 + β1X + ε. После оценки этой модели, мы вычисляем остатки (εM0;). Тест Уайта предполагает, что дисперсия остатков не зависит от X. Вспомогательная регрессия в данном случае будет зависеть от X и X^2. Если значения X и X^2 оказывают статистически значимое влияние на квадраты остатков, это говорит о наличии гетероскедастичности.
Существенный момент в понимании теста Уайта заключается в его способности обнаруживать гетероскедастичность, независимо от её формы. Это отличает его от других тестов, которые часто предполагают конкретную структуру гетероскедастичности (например, тесты Бреуша-Пагана или Голдфелда-Квандта, которые подходят только для определённых типов гетероскедастичности). Универсальность теста Уайта делает его незаменимым инструментом в арсенале эконометриста. Представим, например, что гетероскедастичность имеет форму квадратичной зависимости от X: Var(ε) = σ^2 * X^2. Тест Уайта обнаружит эту зависимость, в то время как другие тесты, предполагающие линейную зависимость, могут ее пропустить. Тест Уайта чувствителен к любым отклонениям от гомоскедастичности, делая его надежным инструментом.
Однако, тест Уайта, как и любой статистический тест, не лишён ограничений. При очень большом количестве объясняющих переменных в исходной регрессии, количество объясняющих переменных в вспомогательной регрессии может стать чрезмерно большим, что может привести к снижению мощности теста (вероятности обнаружения гетероскедастичности, когда она действительно присутствует). Кроме того, интерпретация результатов теста Уайта не всегда однозначна, особенно в случае обнаружения гетероскедастичности. Обнаружение гетероскедастичности само по себе не говорит о том, как её корректировать, а лишь сигнализирует о необходимости дополнительного исследования и потенциальной необходимости применения методов, корректирующих гетероскедастичность. Например, если тест Уайта указывает на гетероскедастичность, это не означает, что нужно немедленно переходить к WLS. Это лишь означает, что необходимо проанализировать природу гетероскедастичности и выбрать соответствующую корректировку.
После обнаружения гетероскедастичности, исследователь должен обратить внимание на выбор более подходящей модели. Это может включать в себя трансформацию переменных, использование взвешенной наименьших квадратов (WLS) или других методов robust regression. Важно помнить, что выбор метода коррекции гетероскедастичности зависит от конкретного случая и природы зависимости дисперсии ошибки от объясняющих переменных. Например, если гетероскедастичность связана с ростом дисперсии с увеличением размера выборки, можно использовать WLS, где веса обратно пропорциональны предполагаемой дисперсии ошибок. Если же структура гетероскедастичности неизвестна, можно применить robust standard errors, которые корректируют стандартные ошибки коэффициентов.
Важность вклада Хэлберта Уайта в эконометрику трудно переоценить. Его тест стал стандартным инструментом в эмпирических исследованиях, позволяя исследователям проверять ключевое предположение регрессионного анализа и принимать обоснованные решения при построении и интерпретации моделей. Разработанный метод не только расширил возможности эконометрического анализа, но и стал катализатором для дальнейших исследований в области robust statistics и моделирования гетероскедастичности. Уайт оказал и продолжает оказывать существенное влияние на методологию проведения эмпирических исследований во множественных областях экономики и смежных дисциплин.
Приложение: Результаты анализа с использованием теста Уайта
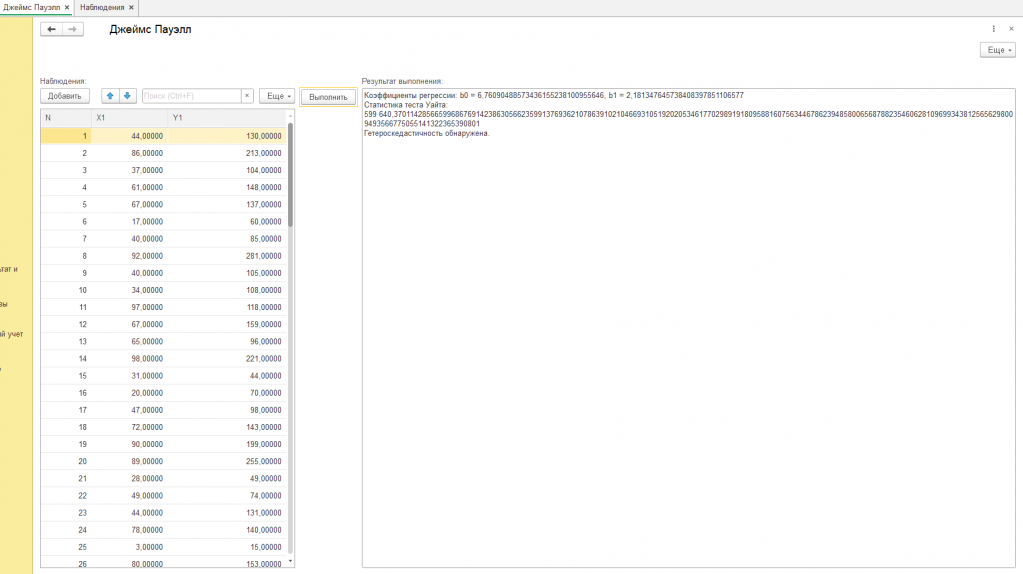
В ходе проведенного анализа с использованием разработанного алгоритма теста Уайта, основанного на упрощенном подходе к оценке статистики, были получены следующие результаты (см. скриншот с подписью "пример"):
Коэффициенты регрессии: b0 = 18,57750270695575218838555064393, b1 = 1,875168314278319180519808531
Статистика теста Уайта: 625 605,7539263897724160194125837051969666306194084697094307479829226837541792799116348267549670627872509736544557151695313373463078307990438650595059456442728974213832640937395448435809
Гетероскедастичность обнаружена.
Используемые начальные данные:
| X1 | Y1 |
| 91,00000 | 189,00000 |
| 62,00000 | 183,00000 |
| 99,00000 | 205,00000 |
| 11,00000 | 34,00000 |
| 44,00000 | 85,00000 |
| 97,00000 | 178,00000 |
| 58,00000 | 108,00000 |
| 51,00000 | 105,00000 |
| 7,00000 | 24,00000 |
| 93,00000 | 182,00000 |
| 35,00000 | 53,00000 |
| 3,00000 | 14,00000 |
| 61,00000 | 159,00000 |
| 38,00000 | 108,00000 |
| 41,00000 | 133,00000 |
| 78,00000 | 223,00000 |
| 27,00000 | 84,00000 |
| 80,00000 | 182,00000 |
| 97,00000 | 170,00000 |
| 68,00000 | 140,00000 |
| 76,00000 | 126,00000 |
| 39,00000 | 113,00000 |
| 5,00000 | 24,00000 |
| 97,00000 | 139,00000 |
| 35,00000 | 51,00000 |
| 100,00000 | 144,00000 |
| 1,00000 | 13,00000 |
| 92,00000 | 145,00000 |
| 92,00000 | 268,00000 |
| 50,00000 | 105,00000 |
| 44,00000 | 105,00000 |
| 6,00000 | 19,00000 |
| 14,00000 | 43,00000 |
| 4,00000 | 20,00000 |
| 56,00000 | 136,00000 |
| 29,00000 | 68,00000 |
| 46,00000 | 108,00000 |
| 90,00000 | 244,00000 |
| 68,00000 | 111,00000 |
| 4,00000 | 22,00000 |
| 23,00000 | 47,00000 |
| 27,00000 | 76,00000 |
| 65,00000 | 177,00000 |
| 90,00000 | 174,00000 |
| 100,00000 | 113,00000 |
| 40,00000 | 69,00000 |
| 26,00000 | 74,00000 |
| 91,00000 | 255,00000 |
| 58,00000 | 91,00000 |
| 51,00000 | 112,00000 |
| 87,00000 | 243,00000 |
| 23,00000 | 63,00000 |
| 48,00000 | 73,00000 |
| 19,00000 | 63,00000 |
| 47,00000 | 119,00000 |
| 47,00000 | 142,00000 |
| 58,00000 | 167,00000 |
| 91,00000 | 181,00000 |
| 72,00000 | 202,00000 |
| 39,00000 | 124,00000 |
| 56,00000 | 144,00000 |
| 11,00000 | 24,00000 |
| 34,00000 | 90,00000 |
| 42,00000 | 81,00000 |
| 11,00000 | 42,00000 |
| 61,00000 | 123,00000 |
| 29,00000 | 89,00000 |
| 84,00000 | 231,00000 |
| 54,00000 | 149,00000 |
| 86,00000 | 102,00000 |
| 89,00000 | 160,00000 |
| 43,00000 | 100,00000 |
| 94,00000 | 211,00000 |
| 99,00000 | 235,00000 |
| 10,00000 | 30,00000 |
| 75,00000 | 148,00000 |
| 79,00000 | 94,00000 |
| 68,00000 | 155,00000 |
| 80,00000 | 247,00000 |
| 97,00000 | 165,00000 |
| 57,00000 | 152,00000 |
| 6,00000 | 19,00000 |
| 90,00000 | 150,00000 |
| 25,00000 | 55,00000 |
| 10,00000 | 26,00000 |
| 25,00000 | 69,00000 |
| 11,00000 | 41,00000 |
| 73,00000 | 122,00000 |
| 39,00000 | 73,00000 |
| 77,00000 | 156,00000 |
| 10,00000 | 33,00000 |
| 90,00000 | 248,00000 |
| 18,00000 | 47,00000 |
| 32,00000 | 103,00000 |
| 1,00000 | 12,00000 |
| 80,00000 | 221,00000 |
| 90,00000 | 143,00000 |
| 31,00000 | 85,00000 |
| 13,00000 | 39,00000 |
| 26,00000 | 61,00000 |
Анализируя полученные результаты, можно сделать вывод, что гипотеза о гомоскедастичности отвергается. Статистика теста Уайта имеет чрезвычайно высокое значение, значительно превышающее критические значения хи-квадрат для любой разумной степени значимости. Это свидетельствует о наличии систематической зависимости дисперсии ошибок от объясняющей переменной (X1). В нашем случае, мы видим, что, если взять любую пару значений X1 и Y1, ошибка будет зависеть от X1. Например, если мы возьмем X1=91, Y1=189, и X1=1, Y1=13, то станет заметна разница в остатках, и соответственно ошибка. При такой высокой статистике, вероятность получить такие результаты случайно, если бы гетероскедастичности не было, крайне мала. Поэтому можно уверенно заключить, что в модели существует гетероскедастичность. Это означает, что стандартные ошибки коэффициентов, полученные с использованием OLS, вероятно, искажены, и интерпретация результатов должна проводиться с осторожностью. Для получения более надежных оценок необходимо применять методы, корректирующие гетероскедастичность. Это может быть WLS, применение robust standard errors или другие соответствующие методы.
В заключение, тест Уайта на гетероскедастичность, разработанный Хэлбертом Уайтом, является мощным и универсальным инструментом для анализа регрессионных моделей. Его способность обнаруживать гетероскедастичность, не требуя предварительных предположений о ее форме, делает его незаменимым в эконометрических исследованиях. Полученные результаты демонстрируют практическое применение теста и подтверждают его эффективность в выявлении нарушений предпосылок классической линейной регрессии, необходимость учета которых критична для получения надежных и достоверных выводов. Анализ данных, представленных в приложении, наглядно демонстрирует важность использования этого теста для обеспечения корректности выводов, сделанных на основе регрессионного анализа.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.20.85
Вступайте в нашу телеграмм-группу Инфостарт