Афиняне! Повсему вижу я, что Вы как-то по-особеному набожны, ибо проходя и осматривая Ваши святыни, я наткнулся и на жертвенник неведомому богу...
Где-то в библии в адрес древних греков...
В общем и целом написать данную статью подвигла меня очередная лекция на тему себестоимости. Кстати, крайне рекомендую курс для ИТ-менеджеров в открытом университете, который там сейчас находится в открытом доступе.
Итак, классика!
Суть в том, что везде, где я встречаю код распределения (размазывания) одной суммы на другую по некому базису, всё всегда сводится к нахождению коэффициента распределения (когда мы делим распределяемую сумму на сумму базы) и последующего умножения этого коэффициента на базу по строке (например, если мы распределяем пропорционально количеству, то на количество).
Таким образом все сводится к такому вот методу:
| Сумма | Количество | Распределенная сумма |
| 100 | 1 | 16,(6) * 1 = 16,67 |
| 200 | 2 | 16,(6) * 2 = 33,33 |
| 300 | 3 | 16,(6) * 3 = 50 |
| итого: 600 | итого: 6 | итого: 100, к = 100/6 = 16,(6) |
Здесь базой является количество, сумма базы = 6, распределяемая сумма = 100. Коэффициент = распределяемая сумма / сумма базы = 100 / 6 = 16,(6) ("Шесть в скобках" - это то, как нас учили записывать периодичские дроби. Если кого-то учили иначе - проьба иметь это ввиду). Далее в каждой строке я округляю результат до копеек.
В принципе мы получили то, что хотели - распределили нужную сумму пропорционально количеству. В данном случае у нас крайне удачно получилось с округлением - в первой строке мы округлили вверх и получили одну лишнюю копейку, во второй строке мы округлили вниз и потеряли копейку. И то, что нам так повезло - это воля парня, сказавшего парню из эпиграфа сказать древним грекам все те умные вещи, о которых он им сказал...
Давайте рассмотрим случай, когда тот парень был к нам не так благосклонен, а именно - давайте распределим 10 на 3:
| Сумма | Количество | Распределенная сумма |
| 100 | 1 | 3,(3) * 1 = 3,33 |
| 200 | 1 | 3,(3) * 1 = 3,33 |
| 250 | 1 | 3,(3) * 1 = 3,33 - добавим разницу 0,01 = 3,34 |
| итого: 550 | итого: 3 | итого: 10? нет! 9,99 + 0,01 = 10, к = 10/3 = 3,(3) |
В итоге у нас не хватило одной копейки. Для того, чтобы решить эту проблему, необходимо учесть остаточек в конце. У нас распределенная сумма получилась равна 9,99, а сумма, которую нужно распределить - 10. Разницу, обычно, добавляют к последней строке. Т.е. в последней строке у нас будет 3,34, "чтобы не нарушать отчетности" (с).
Все хрошо, пока потерянная в ходе округления сумма мала и не играет большой роли. Но если мы попытаемся таким же образом распределить 10 на 30 строк, то внезапно окажется, что к последней строке нам нужно прибавить уже не 1 копейку, а 10. Можно, конечно, прибавить сумму остатка к последней строке:
| № п/п | Сумма | Количество | Распределенная сумма |
| 1 | 100 | 1 | 0,(3) * 1 = 0,33 |
| 2 | 200 | 1 | 0,(3) * 1 = 0,33 |
| 3 | 250 | 1 | 0,(3) * 1 = 0,33 - добавим разницу 0,01 = 3,34 |
| ... | ... | ... | ... |
| 29 | 200 | 1 | 0,(3) * 1 = 0,33 |
| 30 | 100 | 1 | 0,(3) * 1 = 0,33 |
| итого: 30 | итого: 10? нет! 9,90! |
В последней строке в итоге будет сумма 0,33 + 0,10 = 0,43. Если мы распределяем какие-нибудь ксвенные затраты на количество выпуска, то для каждой статьи затрат может набраться весьма большое отклонение, которое все целиком упадет на последнюю строчку. Таким образом продукт, выпущенный нами в последнюю очередь, вберет в свою себестоимость все те отклонения и станет "золотым" )))
Если мы будем дораспределять остаток, то, в принципе, мы также можем попасть на округление и дораспределять нам придется до тх пор, пока все копейки не израсходуются. Это, как мне кажется, несколько неудобно, непрозрачно да и затратно.
Новое решение!
Давным-давно, кажется в позапрошлую работу, меня попросили создать обработку, которая бы перекраивала контуры полей, перераспределяя на их новую площадь какие-то старые остатки на счетах учета затрат на дату распределения. Там как раз сумма распределялась между новыми площадями пропорционально новому метражу. Звучит пространно, но примите на веру (как древние греки), что это относится к обсуждаемой нами задаче распределения суммы по базе. И тогда я как раз "родил" (ага, прям как Авраам Исаака) алгоритм распределения, после которого нет остатка. Странно, но тогдашний мой руководитель так и не понял суть алгоритма, хотя после теста сказал, что все работает и оставил как есть. Западные программисты в таких случаях просто стараются не использовать подобные алгоритмы, так что честь и хвала программистам российским, которые используют и то, в чем не понимают )))
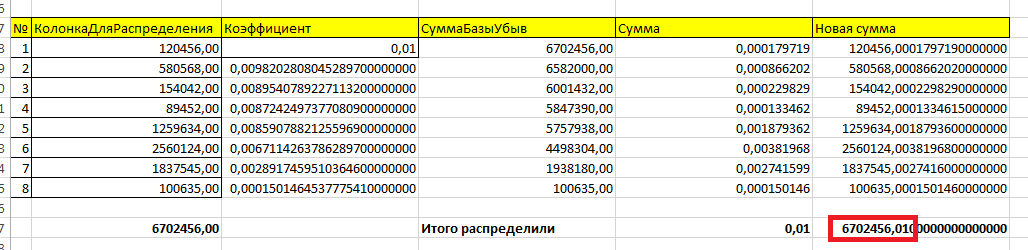
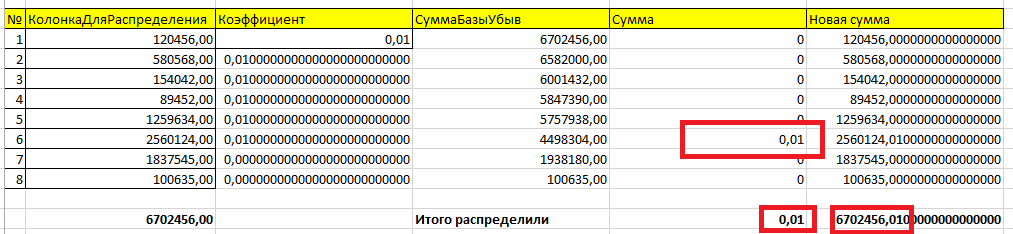
В принципе все просто: мы каждую итерацию должны пересчитывать коэффициент распределения. Давайте построим таблицу с 30-ю записями и добавим колонки для нового коэффициента и по-новому распределенной суммы:
| № п/п | Сумма | Количество | Распределенная сумма | Плавающий коэффициент | По-новому распределенная сумма |
| 1 | 100 | 1 | 0,(3) * 1 = 0,33 | 10/30 = 0,(3) | 0,33 |
| 2 | 200 | 1 | 0,(3) * 1 = 0,33 | 9,67/29 = 0,333448... | 0,33 |
| 3 | 250 | 1 | 0,(3) * 1 = 0,33 | 9,34/28 = 0,333571... | 0,33 |
| ... | ... | ... | ... | ||
| 29 | 200 | 1 | 0,(3) * 1 = 0,33 | 0,67/2 = 0,34 | 0,34 |
| 30 | 100 | 1 | 0,(3) * 1 = 0,33 | 0,33/1 = 0,33 | 0,33 |
| итого: 30 | итого: 9,90 | итого: 10 |
Таким образом у нас больше нет остатка!
Через практическое мессианство! Или перейдем на ты к практике.
Давайте попробуем написать код на языке 1С, который бы распределял сумму ппропорционально базовой колонке таблицы.
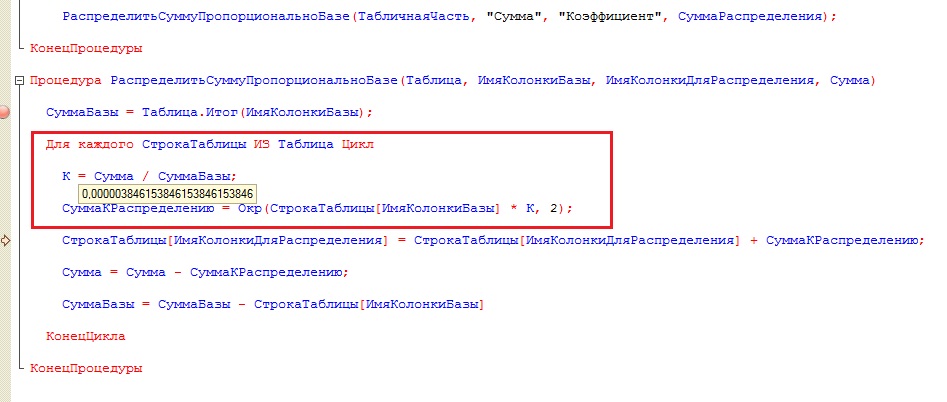
Процедура РаспределитьСуммуПропорциональноБазе(Таблица, ИмяКолонкиБазы, ИмяКолонкиДляРаспределения, Сумма)
СуммаБазы = Таблица.Итог(ИмяКолонкиБазы);
Для каждого СтрокаТаблицы ИЗ Таблица Цикл
К = Сумма / СуммаБазы;
СуммаКРаспределению = Окр(СтрокаТаблицы[ИмяКолонкиБазы] * К, 2);
СтрокаТаблицы[ИмяКолонкиДляРаспределения] = СтрокаТаблицы[ИмяКолонкиДляРаспределения] + СуммаКРаспределению;
Сумма = Сумма - СуммаКРаспределению;
СуммаБазы = СуммаБазы - СтрокаТаблицы[ИмяКолонкиБазы]
КонецЦикла
КонецПроцедуры
Вот такой вот незамысловатый код получился. И можно забыть про контроль остатка нераспределившейся суммы.
В качестве постскриптума...
Этот алгоритм был навеян мне целочисленным алгоритмом построения линии, т.к. в нем Х распределяется на У (или наоборот - при оптимизации вообще пишут два варианта, учитывая, какое смещение больше - по Х или по У).
Вступайте в нашу телеграмм-группу Инфостарт